Lineare zeitinvariante Systeme/Laplace–Rücktransformation: Unterschied zwischen den Versionen
| Zeile 78: | Zeile 78: | ||
*Aufgrund der Fehlanpassung kommt es zur rücklaufenden Welle (Reflexion) $U_←(x)$ vom Leitungsende zum Sender, in der Grafik grün markiert. Für diese gilt am Ausgangspunkt $x = l$: | *Aufgrund der Fehlanpassung kommt es zur rücklaufenden Welle (Reflexion) $U_←(x)$ vom Leitungsende zum Sender, in der Grafik grün markiert. Für diese gilt am Ausgangspunkt $x = l$: | ||
$$U_{\leftarrow}(x = l) = {U_{\rightarrow}(x = l)}\cdot \frac{Z_2 -Z_{\rm W}(f)}{Z_2 + Z_{\rm W}(f)}\hspace{0.05cm}.$$ | $$U_{\leftarrow}(x = l) = {U_{\rightarrow}(x = l)}\cdot \frac{Z_2 -Z_{\rm W}(f)}{Z_2 + Z_{\rm W}(f)}\hspace{0.05cm}.$$ | ||
| − | *Die resultierende (blaue) Welle $U(x)$ ergibt sich aus der phasenrichtigen Addition dieser beiden für sich allein nicht sichtbaren Anteile. Mit zunehmendem $x$ wird $U(x)$ ebenso wie $U_→(x)$ wegen der Leitungsdämpfung kleiner. Auch die rücklaufende Welle $U_←(x)$ wird mit zunehmender Länge gedämpft, allerdings von rechts nach links. | + | *Die resultierende (blaue) Welle $U(x)$ ergibt sich aus der phasenrichtigen Addition dieser beiden für sich allein nicht sichtbaren Anteile. Mit zunehmendem $x$ wird $U(x)$ ebenso wie $U_→(x)$ wegen der Leitungsdämpfung kleiner. Auch die rücklaufende Welle $U_←(x)$ wird mit zunehmender Länge gedämpft, allerdings von rechts nach links. |
| + | {{end}} | ||
| + | |||
| + | ==Verlustlose und verlustarme Leitungen== | ||
| + | Für sehr kurze Koaxialleitungen, wie sie für Verbindungen von HF–Messgeräten im Labor verwendet werden, kann von $R' = G' ≈$ 0 ausgegangen werden. Man spricht dann von einer verlustlosen Leitung. Für eine solche vereinfachen sich die obigen Gleichungen zu | ||
| + | $$\alpha(f) = 0\hspace{0.05cm}, \hspace{0.3cm}\beta(f) = 2\pi \cdot f \cdot \sqrt{L' \cdot C' }\hspace{0.05cm}, \hspace{0.3cm} Z_{\rm W}(f) = \sqrt{{L'}/{ C'} }\hspace{0.05cm}.$$ | ||
| + | |||
| + | Sind $L'$ und $C'$ im betrachteten Frequenzbereich konstant, so ist der (reelle) Wellenwiderstand $Z_W(f)$ ebenfalls frequenzunabhängig und das Phasenmaß $β(f)$ proportional zur Frequenz. Das bedeutet, dass eine verlustlose Leitung stets verzerrungsfrei ist. Das Ausgangssignal weist gegenüber dem Eingangssignal lediglich eine Laufzeit auf. Üblich sind Wellenwiderstände von 50 Ω, 75 Ω und 150 Ω. | ||
| + | |||
| + | Betrachten wir nun nochmals die Formel für das Dämpfungsmaß, also die Dämpfungsfunktion pro Länge, | ||
| + | $$\alpha(f) = {{\rm a}(f)}/{ l} \hspace{0.05cm},$$ | ||
| + | wenn die Leitung etwas länger ist, aber noch nicht als lang bezeichnet werden kann. Man spricht in diesem Fall von einer verlustarmen Leitung. | ||
| + | |||
| + | Die vorne angegebene Formel für das Dämpfungsmaß soll nun für den nicht ganz der Wirklichkeit entsprechenden Fall konstanter Leitungsbeläge ausgewertet werden. Oberhalb einer '''charakteristischen Frequenz''' $f_∗$, die von $R', L', G'$ und $C'$ abhängt, kann $R'$ als sehr klein gegenüber $ωL'$ und $G'$ als sehr klein gegenüber $ωC'$ angenommen werden. Damit ergibt sich die Näherungsformel | ||
| + | $$\alpha_{_{{\rm I}}}(f) = \frac{1}{2} \cdot \left [R' \cdot \sqrt{\frac{C'}{ L'} } + G' \cdot \sqrt{\frac{L'}{ C'} }\right ] \hspace{0.05cm},$$ | ||
| + | die in der Literatur häufig als '''schwache Dämpfung''' bezeichnet wird. | ||
| + | |||
| + | Für kleine Frequenzen $(f < f_∗)$ ist dagegen $R' >> ωL'$ und $G' >> ωC'$ zu berücksichtigen und man erhält eine zweite obere Schranke, die man oft als '''starke Dämpfung''' bezeichnet: | ||
| + | |||
| + | [[Datei:P_ID1795__LZI_T_4_1_S3_kleiner_neu.png | Dämpfungsmaß α(f) und Schranken | rechts]] | ||
| + | |||
| + | $$\alpha_{_{{\rm II}}}(f) = \sqrt{\omega \cdot \frac{R' \hspace{0.05cm} C'}{ 2} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ | ||
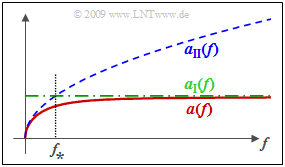
| + | Die Grafik zeigt das Dämpfungsmaß $α(f)$ bei konstanten Leitungsbelägen nach der exakten, aber komplizierten Formel und die beiden Schranken $α_I(f)$ und $α_{II}(f)$. | ||
| + | |||
| + | Man erkennt aus dieser Darstellung: | ||
| + | *Sowohl $α_I(f)$ als auch $α_{II}(f)$ sind obere Schranken für $α(f)$. | ||
| + | *Die charakteristische Frequenz $f_∗$ ist der Schnittpunkt von $α_I(f)$ und $α_{II}(f)$. | ||
| + | *Für $f >> f_∗$ gilt $α(f) ≈ α_I(f)$, für $f << f_∗$ dagegen $α(f) ≈ α_{II}(f)$. | ||
| + | |||
Version vom 9. Mai 2016, 18:28 Uhr
Inhaltsverzeichnis
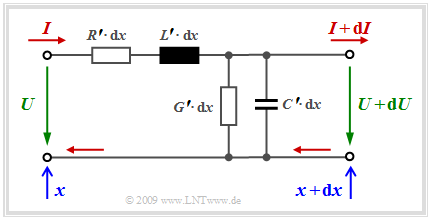
Ersatzschaltbild eines kurzen Leitungsabschnitts (1)
Zur Herleitung der Leitungsgleichungen wird zunächst ein sehr kurzer Leitungsabschnitt der Länge $dx$ betrachtet, so dass sich die Werte für Spannung und Strom am Leitungsanfang $(U$ bzw. $I$ bei $x)$ und am Leitungsende $(U + dU$ sowie $I + dI$ bei $x + dx)$ nur geringfügig unterscheiden. Die Grafik zeigt das zugrundeliegende Modell.
Anders ausgedrückt: Die Leitungslänge $dx$ sei sehr klein gegenüber der Wellenlänge der sich entlang der Leitung ausbreitenden elektromagnetischen Welle, die sich ergibt, da
- mit dem Strom ein magnetisches Feld verbunden ist,
- die Spannung zwischen den Leitern ein elektrisches Feld bewirkt.
Alle infinitesimalen „Bauelemente” im oben skizzierten Ersatzschaltbild sind bei homogenen Leitungen ortsunabhängig:
- Die Induktivität des betrachteten Leitungsabschnitts beträgt $L' · dx$, wobei man die auf die Länge $dx$ bezogene Größe als Induktivitätsbelag bezeichnet.
- Ebenso ist der Kapazitätsbelag $C'$ eine infinitesimal kleine Größe, der ebenso wie $L'$ nur relativ wenig von der Frequenz abhängt.
- Der Ableitungsbelag $G'$ berücksichtigt die Verluste des Dielektrikums zwischen den Drähten. Er nimmt etwa proportional mit der Frequenz zu.
- Den weitaus größten Einfluss auf die Signalübertragung hat der Widerstandsbelag $R'$, der für hohe Frequenzen aufgrund des dann dominanten Skineffekts nahezu proportional mit der Wurzel der Frequenz ansteigt.
Ersatzschaltbild eines kurzen Leitungsabschnitts (2)
Aus den Maschen– und Knotengleichungen des Leitungsabschnitts ergeben sich mit $ω = 2πf$ die beiden Differenzengleichungen $$ \begin{align*} U & = I \cdot (R' + {\rm j} \cdot \omega L') \cdot {\rm d}x + (U + {\rm d}U)\hspace{0.05cm},\\ I & = (U + {\rm d}U) \cdot (G' + {\rm j} \cdot \omega C') \cdot {\rm d}x + (I + {\rm d}I)\hspace{0.05cm} \end{align*}$$. Für einen sehr kurzen Leitungsabschnitt (infinitesimal kleines $dx$) und bei Vernachlässigung der kleinen Größen zweiter Ordnung (zum Beispiel $dU · dx$) kann man nun zwei Differentialquotienten bilden, deren gemeinsame Betrachtung zu einer linearen Differentialgleichung zweiter Ordnung führt: $$\frac{ {\rm d}U}{ {\rm d}x} = - (R' + {\rm j} \cdot \omega L') \cdot I,\hspace{0.5cm} \frac{ {\rm d}I}{ {\rm d}x} = - (G' + {\rm j} \cdot \omega C') \cdot U$$ $$\Rightarrow \hspace{0.3cm}\frac{{\rm d}^2U}{{\rm d}x^2} = (R' + {\rm j} \cdot \omega L') \cdot (G' + {\rm j} \cdot \omega C') \cdot U\hspace{0.05cm}.$$ Die Lösung dieser Differentialgleichung lautet: $$U(x) = U_{\rightarrow}(x=0) \cdot {\rm e}^{-\hspace{0.02cm}\gamma \hspace{0.03cm} \cdot \hspace{0.05cm}x} + U_{\leftarrow}(x=0) \cdot {\rm e}^{\gamma \hspace{0.03cm} \cdot \hspace{0.05cm}x} \hspace{0.05cm}.$$
Der Spannungsverlauf hängt außer vom Ort $x$ auch von der Frequenz $f$ ab, was hier nicht explizit vermerkt ist. Formelmäßig erfasst wird diese Frequenzabhängigkeit durch das Übertragungsmaß
$$\gamma(f) = \sqrt{(R' + {\rm j} \cdot 2\pi f \cdot L') \cdot (G' + {\rm j} \cdot 2\pi f \cdot C')} = \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$
Die beiden letzten Gleichungen beschreiben gemeinsam den Spannungsverlauf entlang der Leitung, der sich aus der Überlagerung einer in positiver $x$–Richtung laufenden Welle $U_→(x)$ und der Welle $U_←(x)$ in Gegenrichtung zusammensetzt.
Der Realteil $α(f)$ des komplexen Übertragungsmaßes $γ(f)$ dämpft die sich ausbreitende Welle und wird daher Dämpfungsmaß genannt. Diese stets gerade Funktion $⇒ α(–f) = α(f)$ ergibt sich aus obiger $γ(f)$–Gleichung wie folgt: $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ Der ungerade Imaginärteil $⇒ β(– f) = – β(f)$ heißt Phasenmaß und beschreibt die Phasendrehung der Welle entlang der Leitung: $$\beta(f) = \sqrt{\frac {1}{2}\cdot \left (-R' G' + \omega^2 \cdot L' C'\right)+ \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
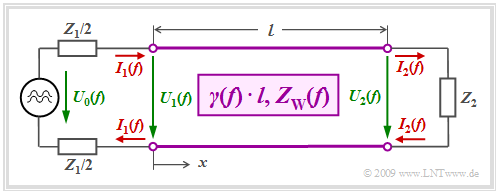
Wellenwiderstand und Reflexionen (1)
Betrachten wir nun eine homogene Leitung der Länge $l$, an dessen Eingang eine harmonische Schwingung $U_0(f)$ mit variabler Frequenz $f$ angelegt wird. Der Sender besitzt den Innenwiderstand $Z_1$, der Empfänger den Eingangswiderstand $Z_2$, der gleichzeitig den Abschlusswiderstand der Leitung bildet. Wir gehen vereinfachend davon aus, dass $Z_1$ und $Z_2$ reelle Widerstände sind.
Strom und Spannung von hinlaufender und rücklaufender Welle sind jeweils über den Wellenwiderstand $Z_W(f)$ miteinander verknüpft: $$I_{\rightarrow}(x, f) = \frac{U_{\rightarrow}(x, f)}{Z_{\rm W}(f)}\hspace{0.05cm}, \hspace{0.5cm} I_{\leftarrow}(x, f) = \frac{U_{\leftarrow}(x, f)}{Z_{\rm W}(f)}\hspace{0.05cm}.$$ Für den Wellenwiderstand gilt dabei: $$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
Die in positiver x–Richtung laufende Welle wird durch die Wechselspannungsquelle am Leitungsanfang (also bei $x =$ 0) erzeugt. Die rücklaufende Welle entsteht erst durch Reflektion der Vorwärtswelle am Leitungsende $(x = l)$. An dieser Stelle wird durch den Abschlusswiderstand $Z_2$ ein festes Verhältnis zwischen Spannung und Strom entsprechend $U_2(f) = Z_2 · I_2(f)$ erzwungen.
Die rücklaufende Welle entsteht bei Fehlanpassung durch Reflexion am Leitungsende: $$U_{\leftarrow}(x = l) = {U_{\rightarrow}(x = l)}\cdot \frac{Z_2 -Z_{\rm W}(f)}{Z_2 + Z_{\rm W}(f)}\hspace{0.05cm}.$$
Man erkennt aus dieser Gleichung, dass nur für $Z_2 = Z_W(f)$ keine rücklaufende Welle entsteht. Eine solche Widerstandanpassung wird in der Nachrichtentechnik stets angestrebt. Allerdings ist diese Anpassung wegen der Frequenzabhängigkeit des Wellenwiderstandes bei festem Abschluss $Z_2$ nicht über einen größeren Frequenzbereich möglich.
Nachfolgend werden diese Gleichungen an einem Beispiel erläutert.
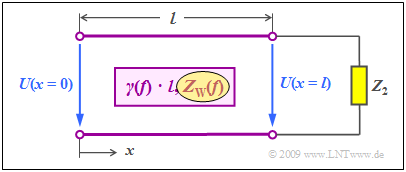
Wellenwiderstand und Reflexionen (2)
Wir betrachten den Fall, dass sich der Abschlusswiderstand $Z_2$ der Leitung (gleichzeitig der Eingangswiderstand des nachfolgenden Empfängers) vom Wellenwiderstand $Z_W(f)$ unterscheidet. Die Fehlanpassung am Leitungsanfang lassen wir außer Betracht.
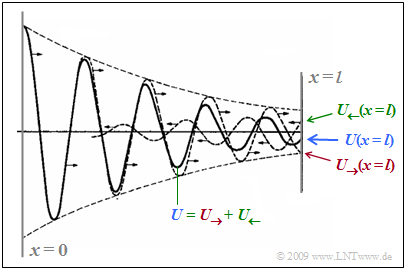
Die untere Grafik aus [Han08] soll deutlich machen, wie sich die resultierende Welle $U(x)$ – als durchgezogene Kurve dargestellt – von der hinlaufenden Welle $U_→(x)$ unterscheidet.
- Rot markiert ist die hinlaufende Welle $U_→(x)$, die ausgehend vom Sender $⇒ U_→(x =$ 0) sich längs der Leitung abschwächt. $U_→(x = l)$ bezeichnet die Welle am Leitungsende.
- Aufgrund der Fehlanpassung kommt es zur rücklaufenden Welle (Reflexion) $U_←(x)$ vom Leitungsende zum Sender, in der Grafik grün markiert. Für diese gilt am Ausgangspunkt $x = l$:
$$U_{\leftarrow}(x = l) = {U_{\rightarrow}(x = l)}\cdot \frac{Z_2 -Z_{\rm W}(f)}{Z_2 + Z_{\rm W}(f)}\hspace{0.05cm}.$$
- Die resultierende (blaue) Welle $U(x)$ ergibt sich aus der phasenrichtigen Addition dieser beiden für sich allein nicht sichtbaren Anteile. Mit zunehmendem $x$ wird $U(x)$ ebenso wie $U_→(x)$ wegen der Leitungsdämpfung kleiner. Auch die rücklaufende Welle $U_←(x)$ wird mit zunehmender Länge gedämpft, allerdings von rechts nach links.
Verlustlose und verlustarme Leitungen
Für sehr kurze Koaxialleitungen, wie sie für Verbindungen von HF–Messgeräten im Labor verwendet werden, kann von $R' = G' ≈$ 0 ausgegangen werden. Man spricht dann von einer verlustlosen Leitung. Für eine solche vereinfachen sich die obigen Gleichungen zu $$\alpha(f) = 0\hspace{0.05cm}, \hspace{0.3cm}\beta(f) = 2\pi \cdot f \cdot \sqrt{L' \cdot C' }\hspace{0.05cm}, \hspace{0.3cm} Z_{\rm W}(f) = \sqrt{{L'}/{ C'} }\hspace{0.05cm}.$$
Sind $L'$ und $C'$ im betrachteten Frequenzbereich konstant, so ist der (reelle) Wellenwiderstand $Z_W(f)$ ebenfalls frequenzunabhängig und das Phasenmaß $β(f)$ proportional zur Frequenz. Das bedeutet, dass eine verlustlose Leitung stets verzerrungsfrei ist. Das Ausgangssignal weist gegenüber dem Eingangssignal lediglich eine Laufzeit auf. Üblich sind Wellenwiderstände von 50 Ω, 75 Ω und 150 Ω.
Betrachten wir nun nochmals die Formel für das Dämpfungsmaß, also die Dämpfungsfunktion pro Länge, $$\alpha(f) = {{\rm a}(f)}/{ l} \hspace{0.05cm},$$ wenn die Leitung etwas länger ist, aber noch nicht als lang bezeichnet werden kann. Man spricht in diesem Fall von einer verlustarmen Leitung.
Die vorne angegebene Formel für das Dämpfungsmaß soll nun für den nicht ganz der Wirklichkeit entsprechenden Fall konstanter Leitungsbeläge ausgewertet werden. Oberhalb einer charakteristischen Frequenz $f_∗$, die von $R', L', G'$ und $C'$ abhängt, kann $R'$ als sehr klein gegenüber $ωL'$ und $G'$ als sehr klein gegenüber $ωC'$ angenommen werden. Damit ergibt sich die Näherungsformel $$\alpha_{_[[:Vorlage:\rm I]]}(f) = \frac{1}{2} \cdot \left [R' \cdot \sqrt{\frac{C'}{ L'} } + G' \cdot \sqrt{\frac{L'}{ C'} }\right ] \hspace{0.05cm},$$ die in der Literatur häufig als schwache Dämpfung bezeichnet wird.
Für kleine Frequenzen $(f < f_∗)$ ist dagegen $R' >> ωL'$ und $G' >> ωC'$ zu berücksichtigen und man erhält eine zweite obere Schranke, die man oft als starke Dämpfung bezeichnet:
$$\alpha_{_[[:Vorlage:\rm II]]}(f) = \sqrt{\omega \cdot \frac{R' \hspace{0.05cm} C'}{ 2} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$ Die Grafik zeigt das Dämpfungsmaß $α(f)$ bei konstanten Leitungsbelägen nach der exakten, aber komplizierten Formel und die beiden Schranken $α_I(f)$ und $α_{II}(f)$.
Man erkennt aus dieser Darstellung:
- Sowohl $α_I(f)$ als auch $α_{II}(f)$ sind obere Schranken für $α(f)$.
- Die charakteristische Frequenz $f_∗$ ist der Schnittpunkt von $α_I(f)$ und $α_{II}(f)$.
- Für $f >> f_∗$ gilt $α(f) ≈ α_I(f)$, für $f << f_∗$ dagegen $α(f) ≈ α_{II}(f)$.