Lineare zeitinvariante Systeme/Laplace–Rücktransformation: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Problemstellung und Voraussetzungen== | ==Problemstellung und Voraussetzungen== | ||
| − | Das Kapitel 3.3 behandelt die folgende Problemstellung: Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p) in der Pol–Nullstellen–Form. Gesucht ist die '''Laplace–Rücktransformierte''', die die dazugehörige Zeitfunktion $y(t)$ angibt und die in diesem Tutorial wie folgt bezeichnet wird: | + | Das Kapitel 3.3 behandelt die folgende Problemstellung: Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. Gesucht ist die '''Laplace–Rücktransformierte''', die die dazugehörige Zeitfunktion $y(t)$ angibt und die in diesem Tutorial wie folgt bezeichnet wird: |
$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} | $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} | ||
y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$ | y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$ | ||
Version vom 12. Mai 2016, 11:16 Uhr
Problemstellung und Voraussetzungen
Das Kapitel 3.3 behandelt die folgende Problemstellung: Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. Gesucht ist die Laplace–Rücktransformierte, die die dazugehörige Zeitfunktion $y(t)$ angibt und die in diesem Tutorial wie folgt bezeichnet wird: $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$
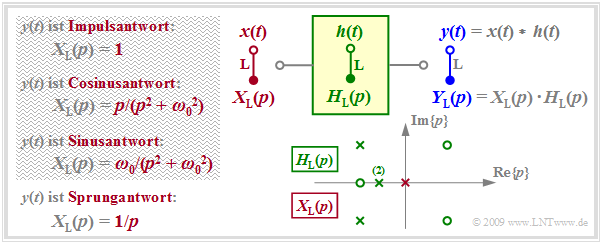
In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt: