Lineare zeitinvariante Systeme/Eigenschaften von Kupfer–Doppeladern: Unterschied zwischen den Versionen
| Zeile 100: | Zeile 100: | ||
$$\begin{align*} H_{\alpha 0}(f) & = {\rm e}^{-\alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l}= {\rm e}^{-{\rm a}_0}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_0= \alpha_0\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l,\\ H_{\alpha 1}(f) & = {\rm e}^{-\alpha_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_1 \cdot 2f/R}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_1 = \alpha_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot {R}/{2} \hspace{0.05cm},\\ H_{\beta 1}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \beta_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l} = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}\tau_{\rm P}} \hspace{0.05cm},\hspace{0.2cm} \tau_{\rm P} = \frac{\beta_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l }{2 \pi} \hspace{0.05cm},\\ H_{\alpha 2}(f) & = {\rm e}^{-\alpha_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_2 = \alpha_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm},\\ H_{\beta 2}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\beta_2 \hspace{0.05cm \cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} b_2 = \beta_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm}. \end{align*}$$ | $$\begin{align*} H_{\alpha 0}(f) & = {\rm e}^{-\alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l}= {\rm e}^{-{\rm a}_0}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_0= \alpha_0\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l,\\ H_{\alpha 1}(f) & = {\rm e}^{-\alpha_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_1 \cdot 2f/R}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_1 = \alpha_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot {R}/{2} \hspace{0.05cm},\\ H_{\beta 1}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \beta_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l} = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}\tau_{\rm P}} \hspace{0.05cm},\hspace{0.2cm} \tau_{\rm P} = \frac{\beta_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l }{2 \pi} \hspace{0.05cm},\\ H_{\alpha 2}(f) & = {\rm e}^{-\alpha_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_2 = \alpha_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm},\\ H_{\beta 2}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\beta_2 \hspace{0.05cm \cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} b_2 = \beta_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm}. \end{align*}$$ | ||
| + | Auf die Bedeutung der hier implizit definierten Größen wird etwas später eingegangen. | ||
| + | |||
| + | Wir gehen hier zunächst ganz formal vor. Nach dem Faltungssatz gilt für die resultierende Impulsantwort als die Fourierrücktransformierte von $H_{\rm K}(f)$: | ||
| + | $$h_{\rm K}(t) = h_{\alpha 0}(t) \star h_{\alpha 1}(t) \star h_{\beta 1}(t)\star h_{\alpha 2}(t) \star h_{\beta 2}(t) \hspace{0.05cm},$$ | ||
| + | $$h_{\alpha 0}(t) \quad \circ\!\!-\!\!\!\!\!\!-\!\!\bullet\quad H_{\alpha 0}(f) \hspace{0.05cm},\hspace{0.2cm} h_{\alpha 1}(t) \circ\!\!-\!\!\!\!\!\!-\!\!\bullet\quad H_{\alpha 1}(f) \hspace{0.05cm},\hspace{0.2cm} {\rm usw.}$$ | ||
| + | |||
| + | Diese fünf Anteile sollen nun separat betrachtet werden, wobei sich die numerischen Ergebnisse auf ein digitales Übertragungssystem mit der Bitrate $R =$ 30 Mbit/s und eine Zweidrahtleitung 0.4 mm der Länge $l =$ 1 km beziehen. Damit lauten die $α$–Koeffizienten in Neper: | ||
| + | $$\alpha_0 = 0.59\, \frac{{\rm Np}}{{\rm km}} \hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.10\, \frac{{\rm Np}}{{\rm km \cdot MHz}}\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 1.69\, \frac{{\rm Np}}{{\rm km \cdot MHz^{0.5}}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Das Phasenmaß dieser Leitung ist ebenfalls in [PW95] angegeben: | ||
| + | $$b_{\rm K}(f) = \beta_1 \cdot f + \beta_2 \cdot \sqrt {f}\hspace{0.05cm}, \hspace{0.2cm} \beta_1 = 32.9\, \frac{{\rm rad}}{{\rm km \cdot MHz}}\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 2.26\, \frac{{\rm rad}}{{\rm km \cdot MHz^{0.5}}}\hspace{0.05cm}.$$ | ||
| + | Als Normierungsgröße der Zeit eignet sich die Symboldauer $T = 1/R ≈$ 33 ns. | ||
{{Display}} | {{Display}} | ||
Version vom 14. Mai 2016, 12:09 Uhr
Inhaltsverzeichnis
Zugangsnetz eines Telekommunikationssystems (1)
Bei einem Telekommunikationssystem unterscheidet man zwischen
- dem Fern– und Regionalnetz sowie
- dem Teilnehmeranschlussbereich,
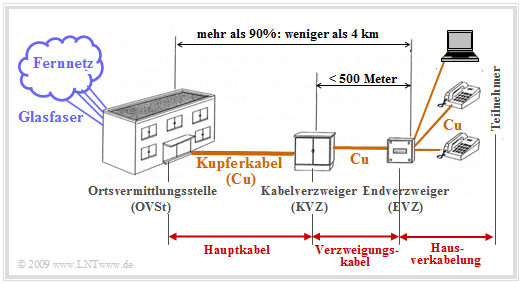
die durch die Ortsvermittlungsstelle voneinander getrennt sind. Die Grafik zeigt die Netzinfrastruktur bei $\href{https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=buchseite&due=inhalt&zustand=1921&session_id=}{ISDN}$ (Integrated Services Digital Network).
Ursprünglich basierte das gesamte Fernsprechnetz auf Kupferleitungen. Mitte der 1980–Jahre wurden aber im Weitverkehr die – vorwiegend koaxialen – Kupferkabel durch Glasfaserkabel ersetzt, da der stetig wachsende Bandbreitebedarf nur mit optischer Übertragungstechnik befriedigt werden konnte.
Aufgrund der immens hohen Verlegekosten sind Glasfasern im Teilnehmeranschlußbereich bis heute (2009) nicht wirtschaftlich, allerdings gibt es schon lange Planungen zu Fiber–to–the–Building (FttB) bzw. Fiber–to–the–Home (FttH). Vielmehr ist man in den letzten 20 Jahren den Weg gegangen, durch die Entwicklung und die Verbesserung hochratiger Übertragungssysteme wie $\href{https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=buchseite&due=inhalt&zustand=1967&session_id=}{DSL}$ (Digital Subscriber Line) über das konventionelle, kupferbasierte Zugangsnetz ausreichend Kapazität bereitzustellen.
Zugangsnetz eines Telekommunikationssystems (2)
In Deutschland ist diese so genannte „Last Mile” im Landesdurchschnitt kürzer als 4 km, in städtischen Gebieten zu 90% sogar kürzer als 2.8 km. Der Teilnehmeranschlußbereich setzt sich meist wie folgt zusammen:
- das Hauptkabel mit bis zu 2000 Doppeladern als Verbindung zwischen Ortsvermittlungsstelle und dem Kabelverzweiger,
- das Verzweigungskabel zwischen Kabel– und Endverzweiger, mit bis zu 300 Doppeladern und mit maximal 500 Metern deutlich kürzer als ein Hauptkabel,
- das Hausanschlußkabel zwischen Endverzweiger und der Netzabschlußdose beim Teilnehmer mit zwei Doppeladern.
Zur Verminderung des Nebensprechens auf benachbarte Leitungspaare durch induktive und kapazitive Kopplungen und zur Erhöhung der Packungsdichte werden jeweils zwei Doppeladern zu einem so genannten Sternvierer verseilt. Die untere Grafik zeigt einen solchen Sternvierer und ein Bündelkabel. Hier werden je fünf solcher Vierer zu einem Grundbündel und je 5 Grundbündel zu einem Hauptbündel zusammengefasst. Dieses beinhaltet somit 50 Doppeladern mit PE–Isolierung (PE: Polyethylen).
Dämpfungsmaß von Zweidrahtleitungen
Das Dämpfungsmaß $α(f)$ und der Wellenwiderstand $Z_{\rm W}(f)$ von Doppeladern in realen verlegten Kabeln weichen mehr oder weniger stark von der in $\href{http://www.lntwww.de/Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie}{Kapitel 4.1}$ dargelegten Theorie ab. Gründe hierfür sind:
- komplexe Vorgänge der Wirbelstrombildung und der Stromverdrängung, und
- Inhomogenitäten im Kabelaufbau bei gespleißten Kabelabschnitten.
Verschiedene Netzbetreiber haben $α(f)$ und $Z_{\rm W}(f)$ gemessen und daraus empirische Gleichungen abgeleitet. Wir beziehen uns hier auf die in $\href{https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=entitaet&e_id=25355&hyperlink_typ=entitaet_verweis&session_id=}{[PW95]}$ dokumentierten Arbeiten von M. Pollakowski und H.W. Wellhausen vom Fernmeldetechnischen Zentralamt der Deutschen Bundespost in Darmstadt. Diese ermittelten für unterschiedliche Leitungsdurchmesser $d$ unter anderem das empirische Dämpfungsmaß aus 40 Messungen im Frequenzbereich bis 30 MHz entsprechend der Gleichung
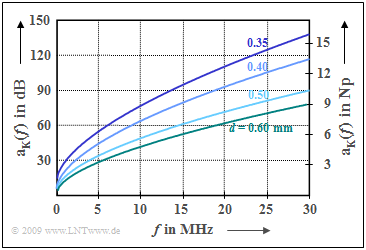
$$\alpha (f) = k_1 + k_2 \cdot (f/{\rm MHz})^{k_3} \hspace{0.05cm}.$$ Die Grafik zeigt die Messergebnisse:
- $d =$ 0.35 mm: $k_1 =$ 7.9 dB/km, $k_2 =$ 15.1 dB/km, $k_3 =$ 0.62,
- $d =$ 0.40 mm: $k_1 =$ 5.1 dB/km, $k_2 =$ 14.3 dB/km, $k_3 =$ 0.59,
- $d =$ 0.50 mm: $k_1 =$ 4.4 dB/km, $k_2 =$ 10.8 dB/km, $k_3 =$ 0.60,
- $d =$ 0.60 mm: $k_1 =$ 3.8 dB/km, $k_2 =$ 9.2 dB/km, $k_3 =$ 0.61.
Man erkennt aus dieser Darstellung:
- Das Dämpfungsmaß $α(f)$ sowie die Dämpfungsfunktion $a_{\rm K}(f) = α(f) · l$ hängt signifikant vom Leitungsdurchmesser ab. Die seit 1994 verlegten Kabel (Durchmessern; 0.35 mm und 0.5 mm) haben etwa ein um 10% größeres Dämpfungsmaß als die älteren Leitungen 0.4 mm und 0.6 mm.
- Dieser mit den Herstellungs– und Verlegungskosten begründete kleinere Leitungsdurchmesser $d$ vermindert allerdings die Reichweite der auf diesen Leitungen eingesetzten Übertragungssysteme signifikant, so dass im schlimmsten Fall teuere Zwischengeneratoren eingesetzt werden müssen, um die Kunden mit hochratigen Diensten versorgen zu können.
- Die heute üblichen Übertragungsverfahren für Kupferleitungen belegen allerdings nur ein relativ schmales Frequenzband, zum Beispiel sind dies bei ISDN 120 kHz und bei DSL ca. 1100 kHz. Für $f =$ 1 MHz beträgt das Dämpfungsmaß für ein 0.4 mm–Kabel etwa 20 dB/km, so dass selbst bei einer Kabellänge von 4 km der Dämpfungswert nicht über 80 dB liegt.
- Eine Ausnahme bildet VDSL, das z. B. die Deutsche Telekom in allen größeren Städten anbietet. Hier geht der Frequenzbereich bis 30 MHz. Deshalb wurden hierfür Glasfaserverbindungen bis zum Kabelverzweiger verlegt, um die noch mit Kupfer zu überbrückende Länge klein zu halten. Man spricht dann von Fibre–to–the–Cabinet (FttC).
Umrechnung zwischen $k$– und $α$– Parametern (1)
Zur Berechnung des Frequenzgangs $H_{\rm K}(f)$ sollte man stets vom gemessenen Dämpfungsmaß $$\alpha (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}= \alpha_{\rm I} (f) \hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz}$$ ausgehen. Will man dagegen die dazugehörige Zeitfunktion in Form der Impulsantwort $h_{\rm K}(t)$ ermitteln, so ist es günstiger (siehe übernächsten Abschnitt), wenn das Dämpfungsmaß in der Form $$\alpha(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}= \alpha_{\rm II} (f)$$ dargestellt werden kann, wie es auch für die Koaxialkabel üblich ist.
Als Kriterium dieser Umrechnung gehen wir davon aus, dass die quadratische Abweichung dieser beiden Funktionen im Bereich von $f =$ 0 bis $f = B$ minimal ist:
$$\int\limits_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$
Es ist offensichtlich, dass $α_0 = k_1$ gelten wird. Die Parameter $α_1$ und $α_2$ sind von der zugrundegelegten Bandbreite $B$ abhängig. Sie lauten entsprechend Aufgabe A4.6:
$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$
Für $k_3 =$ 1 (frequenzproportionales Dämpfungsmaß) ergeben sich folgerichtig
$$\alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} ,$$
während man für $k_3 =$ 0.5 die folgenden Koeffizienten erhält:
$$\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0}}\hspace{0.05cm}.$$
In diesem Fall würde das Dämpfungsmaß $α(f)$ mit der Wurzel aus der Frequenz ansteigen. Es ergäbe sich also der gleiche Verlauf wie bei einem Koaxialkabel entsprechend dem Skineffekt.
Nachfolgend wird an drei Beispielen verdeutlicht, wie die zugrundeliegende Bandbreite $B$ die Ergebnisse dieser Umrechnung beeinflussen.
Umrechnung zwischen $k$– und $α$– Parametern (2)
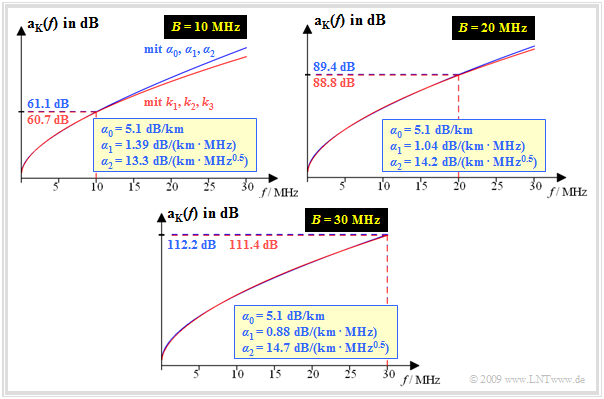
Bei allen nachfolgenden Grafiken gehen wir von der Leitungslänge $l =$ 1 km und vom Durchmesser 0.4 mm aus $⇒ k_1 =$ 5.1 dB/km, $k_2 =$ 14.3 dB/km, $k_3 =$ 0.59. Für diesen Fall zeigt die folgende Grafik die mit $α_0, α_1$ und $α_2$ approximierte Dämpfung (blaue Kurve) im Vergleich zum tatsächlichen Verlauf gemäß $k_1, k_2, k_3$ (rote Kurve). Die drei Diagramme gelten für die Bandbreiten $B =$ 10 MHz, $B =$ 20 MHz und $B =$ 30 MHz. Die ermittelten Koeffizienten $α_1$ und $α_2$ sind angegeben. Stets gilt $α_0 = k_1 =$ 5.1 dB/km.
Man erkennt aus diesen Darstellungen:
- Selbst beim größten Approximationsbereich $(B =$ 30 MHz) nähert die blaue Kurve (mit $α_0, α_1, α_2$) den gemessenen Verlauf (rote Kurve, beschrieben durch $k_1, k_2, k_3$) sehr gut an.
- Bei kleinerer Bandbreite $(B =$ 20 MHz bzw. 10 MHz) ist die Approximation im Bereich 0 $≤ f ≤ B$ noch besser, doch kommt es dann für $f > B$ zu Verfälschungen.
- Der Dämpfungswert $a_{\rm K}(f =$ 30 MHz) ≈ 112.2 dB setzt sich bei der betrachteten Zweidrahtleitung $(l =$ 1 km, $d =$ 0.4 mm) folgendermaßen zusammen: 4.5% geht auf den Gleichsignalkoeffizienten $α_0$ zurück, 23.5% auf den frequenzproportioanlen Anteil $α_1$ und 72% auf den Koeffizienten $α_2$.
- Das Normalkoaxialkabel 2.6/9.5 mm weist im Vergleich dazu erst bei einer Länge von $l =$ 8.7 km eine vergleichbare Dämpfung $a_{\rm K}(f =$ 30 MHz) ≈ 112 dB auf, wobei $α_0$ nur für 0.1% und $α_1$ nur für ca. 1% verantwortlich ist, während der Großteil der Dämpfung vom Skineffekt $(α_2)$ herrührt.
Impulsantworten von Zweidrahtleitungen (1)
Mit dieser Koeffizientenumrechnung $k_1, k_2, k_3 ⇒ α_0, α_1, α_2$ kann nun für den gesamten Frequenzgang einer Zweidrahtleitung geschrieben werden: $$H_{\rm K}(f) = H_{\alpha 0}(f) \cdot H_{\alpha 1}(f) \cdot H_{\beta 1}(f)\cdot H_{\alpha 2}(f) \cdot H_{\beta 2}(f) \hspace{0.05cm}.$$
Hierbei wurden folgende Abkürzungen verwendet: $$\begin{align*} H_{\alpha 0}(f) & = {\rm e}^{-\alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l}= {\rm e}^{-{\rm a}_0}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_0= \alpha_0\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l,\\ H_{\alpha 1}(f) & = {\rm e}^{-\alpha_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_1 \cdot 2f/R}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_1 = \alpha_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot {R}/{2} \hspace{0.05cm},\\ H_{\beta 1}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \beta_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l} = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}\tau_{\rm P}} \hspace{0.05cm},\hspace{0.2cm} \tau_{\rm P} = \frac{\beta_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l }{2 \pi} \hspace{0.05cm},\\ H_{\alpha 2}(f) & = {\rm e}^{-\alpha_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_2 = \alpha_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm},\\ H_{\beta 2}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\beta_2 \hspace{0.05cm \cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} b_2 = \beta_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm}. \end{align*}$$
Auf die Bedeutung der hier implizit definierten Größen wird etwas später eingegangen.
Wir gehen hier zunächst ganz formal vor. Nach dem Faltungssatz gilt für die resultierende Impulsantwort als die Fourierrücktransformierte von $H_{\rm K}(f)$:
$$h_{\rm K}(t) = h_{\alpha 0}(t) \star h_{\alpha 1}(t) \star h_{\beta 1}(t)\star h_{\alpha 2}(t) \star h_{\beta 2}(t) \hspace{0.05cm},$$
$$h_{\alpha 0}(t) \quad \circ\!\!-\!\!\!\!\!\!-\!\!\bullet\quad H_{\alpha 0}(f) \hspace{0.05cm},\hspace{0.2cm} h_{\alpha 1}(t) \circ\!\!-\!\!\!\!\!\!-\!\!\bullet\quad H_{\alpha 1}(f) \hspace{0.05cm},\hspace{0.2cm} {\rm usw.}$$
Diese fünf Anteile sollen nun separat betrachtet werden, wobei sich die numerischen Ergebnisse auf ein digitales Übertragungssystem mit der Bitrate $R =$ 30 Mbit/s und eine Zweidrahtleitung 0.4 mm der Länge $l =$ 1 km beziehen. Damit lauten die $α$–Koeffizienten in Neper: $$\alpha_0 = 0.59\, \frac[[:Vorlage:\rm Np]][[:Vorlage:\rm km]] \hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.10\, \frac[[:Vorlage:\rm Np]][[:Vorlage:\rm km \cdot MHz]]\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 1.69\, \frac[[:Vorlage:\rm Np]]{{\rm km \cdot MHz^{0.5}}} \hspace{0.05cm}.$$
Das Phasenmaß dieser Leitung ist ebenfalls in [PW95] angegeben: $$b_{\rm K}(f) = \beta_1 \cdot f + \beta_2 \cdot \sqrt {f}\hspace{0.05cm}, \hspace{0.2cm} \beta_1 = 32.9\, \frac[[:Vorlage:\rm rad]][[:Vorlage:\rm km \cdot MHz]]\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 2.26\, \frac[[:Vorlage:\rm rad]]{{\rm km \cdot MHz^{0.5}}}\hspace{0.05cm}.$$ Als Normierungsgröße der Zeit eignet sich die Symboldauer $T = 1/R ≈$ 33 ns.