Modulationsverfahren/Zielsetzung von Modulation und Demodulation: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{FirstPage}} {{Header |Untermenü=Allgemeine Beschreibung |Vorherige Seite= |Nächste Seite=Qualitätskriterien }} ==Betrachtetes Nachrichtenübertragungssyst…“) |
|||
| Zeile 16: | Zeile 16: | ||
| − | *Der Kanal kann eine elektrische Leitung (Koaxialkabel, Twisted Pair, usw.), ein Lichtwellenleiter (Multimode– bzw. Monomode–Glasfaser) oder eine Funkverbindung (Richtfunk, Satellitenfunk, Mobilfunk, usw.) sein und wird hier durch seinen Frequenzgang $ | + | *Der Kanal kann eine elektrische Leitung (Koaxialkabel, Twisted Pair, usw.), ein Lichtwellenleiter (Multimode– bzw. Monomode–Glasfaser) oder eine Funkverbindung (Richtfunk, Satellitenfunk, Mobilfunk, usw.) sein und wird hier durch seinen Frequenzgang $H_{\rm K}(f)$ beschrieben. |
| Zeile 32: | Zeile 32: | ||
*Die Demodulation ist die Signalrücksetzung beim Empfänger, um aus dem hochfrequenten Empfangssignal $r(t)$ das niederfrequente Sinkensignal $υ(t) ≈ q(t)$ zu gewinnen. Bei realem Kanal ist aufgrund des stets vorhandenen Rauschens $n(t)$ das Wunschergebnis $υ(t) = q(t)$ nicht möglich. | *Die Demodulation ist die Signalrücksetzung beim Empfänger, um aus dem hochfrequenten Empfangssignal $r(t)$ das niederfrequente Sinkensignal $υ(t) ≈ q(t)$ zu gewinnen. Bei realem Kanal ist aufgrund des stets vorhandenen Rauschens $n(t)$ das Wunschergebnis $υ(t) = q(t)$ nicht möglich. | ||
| + | |||
| + | ==Anpassung an Übertragungskanal und Störspektrum== | ||
| + | Die vorrangige Aufgabe der Modulation (im hier gemeinten Sinne) ist es, das Nachrichtensignal durch Zusetzen eines höherfrequenten Trägersignals mit der Trägerfrequenz $f_{\rm T}$ in eine andere Frequenzlage | ||
| + | *mit günstigerem Frequenzgang $H_{\rm K}(f)$ und/oder | ||
| + | *mit günstigerem Störleistungsdichtespektrum ${\it Φ}_n(f)$ | ||
| + | |||
| + | |||
| + | zu verschieben. Weitere Gründe für Modulation/Demodulation werden in den nachfolgenden Abschnitten genannt. | ||
| + | |||
| + | |||
| + | {{Beispiel}} | ||
| + | Die Grafik zeigt in blau das niederfrequente Spektrum $Q(f)$ mit der Bandbreite $B_{\rm NF}$. Grün eingezeichnet ist der Dämpfungsverlauf $a_{\rm K}(f) = \ –ln |H_{\rm K}(f)|$ des Kanals, der hier in einem ausreichend großen Frequenzbereich günstige Eigenschaften mit konstant geringer Dämpfung zeigt. | ||
| + | |||
| + | |||
| + | :[[Datei: P_ID932__Mod_T_1_1_S2_neu.png | Zur Verdeutlichung von Modulation und Demodulation]] | ||
| + | |||
| + | |||
| + | Ockerfarben sehen Sie das Störleistungsdichtespektrum ${\it Φ}_n(f)$, das wegen des thermischen Rauschens im gesamten Frequenzbereich nicht verschwindet und bei unserem konstruierten Beispiel um die Frequenz $f_{\rm St}$ aufgrund äußerer Störungen besonders große Werte annimmt. | ||
| + | |||
| + | |||
| + | Diese Randbedingungen machen deutlich: | ||
| + | *Man muss die Trägerfrequenz $f_{\rm T}$ in etwa so wählen wie eingezeichnet, damit $S(f)$ bestmöglich hinsichtlich Verzerrungen und Störungen/Rauschen übertragen werden kann. Es ergibt sich so ein Frequenzband ausreichender Qualität der Breite $B_{\rm HF} = 2 · B_{\rm NF}$. | ||
| + | |||
| + | |||
| + | *Diese Verschiebung des Quellensignal–Spektrums $Q(f)$ um die Trägerfrequenz $f_{\rm T}$ nach rechts – und aufgrund der systemtheoretischen Betrachtungsweise beidseitiger Frequenzen auch um den gleicen Abstand nach links – beschreibt die ''Modulation''. | ||
| + | |||
| + | |||
| + | *Dagegen versteht man unter ''Demodulation'' die Signalumsetzung in Gegenrichtung. Ausgehend vom Empfangsspektrum $R(f)$, das sich vom Sendespektrum $S(f)$ aufgrund von Dämpfung und Rauschen zumindest geringfügig unterscheidet, kommt man zur Spektralfunktion $V(f) ≈ Q(f)$. | ||
| + | |||
| + | |||
| + | {{end}} | ||
Version vom 10. Juni 2016, 11:41 Uhr
Betrachtetes Nachrichtenübertragungssystem
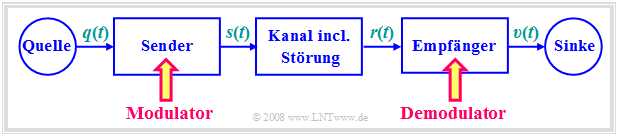
Im gesamten Buch wird von folgendem Blockschaltbild ausgegangen:
Hierzu ist anzumerken:
- Das zur Übertragung anstehende Quellensignal $q(t)$ sei ein Analogsignal, zum Beispiel Sprache, Musik oder der Ausgang einer (analogen) Videokamera. Das zugehörige Spektrum $Q(f)$ sei auf den Frequenzbereich $|f| ≤ B_{\rm NF}$ begrenzt, wobei der Index für „Niederfrequenz” steht.
- Der Kanal kann eine elektrische Leitung (Koaxialkabel, Twisted Pair, usw.), ein Lichtwellenleiter (Multimode– bzw. Monomode–Glasfaser) oder eine Funkverbindung (Richtfunk, Satellitenfunk, Mobilfunk, usw.) sein und wird hier durch seinen Frequenzgang $H_{\rm K}(f)$ beschrieben.
- Der mittlere Block in obigem Bild beinhaltet auch Störungen (Interferenzen, Übersprechen anderer Nutzer, Impulsstörungen durch Starkstromleitungen, etc.) und Rauschquellen wie Widerstands– und Halbleiterrauschen. Diese werden durch das Störleistungsdichtespektrum ${\it Φ}_n(f)$ erfasst.
- Aufgabe eines solchen Nachrichtenübertragungssystems ist es, die im Quellensignal $q(t)$ enthaltene Nachricht bzw. Information – man beachte die unterschiedliche Bedeutung dieser zwei Größen – zur räumlich entfernten Sinke zu übertragen mit der Maßgabe, dass sich das Sinkensignal $υ(t)$ „möglichst wenig” von $q(t)$ unterscheidet.
- Ein häufig auftretendes Problem ist, dass der Übertragungskanal für die direkte Übertragung des Quellensignals $q(t)$ ungeeignet ist, da dieses für ihn ungünstige Frequenzen beinhaltet. So kann ein Musiksignal mit Frequenzen bis ca. 15 kHz nicht direkt per Funk übertragen werden, da eine Funkausbreitung erst ab etwa 100 kHz möglich ist.
- Abhilfe schafft hier nur eine Signalumsetzung beim Sender, die man Modulation nennt. Das Ausgangssignal des Modulators wird im Folgenden einheitlich als das Sendesignal $s(t)$ bezeichnet. Dieses liegt im Allgemeinen bei höheren Frequenzen als das Quellensignal $q(t)$.
- Die Demodulation ist die Signalrücksetzung beim Empfänger, um aus dem hochfrequenten Empfangssignal $r(t)$ das niederfrequente Sinkensignal $υ(t) ≈ q(t)$ zu gewinnen. Bei realem Kanal ist aufgrund des stets vorhandenen Rauschens $n(t)$ das Wunschergebnis $υ(t) = q(t)$ nicht möglich.
Anpassung an Übertragungskanal und Störspektrum
Die vorrangige Aufgabe der Modulation (im hier gemeinten Sinne) ist es, das Nachrichtensignal durch Zusetzen eines höherfrequenten Trägersignals mit der Trägerfrequenz $f_{\rm T}$ in eine andere Frequenzlage
- mit günstigerem Frequenzgang $H_{\rm K}(f)$ und/oder
- mit günstigerem Störleistungsdichtespektrum ${\it Φ}_n(f)$
zu verschieben. Weitere Gründe für Modulation/Demodulation werden in den nachfolgenden Abschnitten genannt.
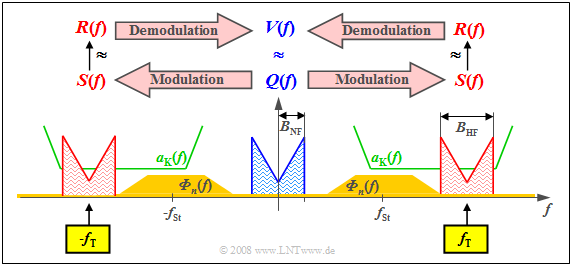
Die Grafik zeigt in blau das niederfrequente Spektrum $Q(f)$ mit der Bandbreite $B_{\rm NF}$. Grün eingezeichnet ist der Dämpfungsverlauf $a_{\rm K}(f) = \ –ln |H_{\rm K}(f)|$ des Kanals, der hier in einem ausreichend großen Frequenzbereich günstige Eigenschaften mit konstant geringer Dämpfung zeigt.
Ockerfarben sehen Sie das Störleistungsdichtespektrum ${\it Φ}_n(f)$, das wegen des thermischen Rauschens im gesamten Frequenzbereich nicht verschwindet und bei unserem konstruierten Beispiel um die Frequenz $f_{\rm St}$ aufgrund äußerer Störungen besonders große Werte annimmt.
Diese Randbedingungen machen deutlich:
- Man muss die Trägerfrequenz $f_{\rm T}$ in etwa so wählen wie eingezeichnet, damit $S(f)$ bestmöglich hinsichtlich Verzerrungen und Störungen/Rauschen übertragen werden kann. Es ergibt sich so ein Frequenzband ausreichender Qualität der Breite $B_{\rm HF} = 2 · B_{\rm NF}$.
- Diese Verschiebung des Quellensignal–Spektrums $Q(f)$ um die Trägerfrequenz $f_{\rm T}$ nach rechts – und aufgrund der systemtheoretischen Betrachtungsweise beidseitiger Frequenzen auch um den gleicen Abstand nach links – beschreibt die Modulation.
- Dagegen versteht man unter Demodulation die Signalumsetzung in Gegenrichtung. Ausgehend vom Empfangsspektrum $R(f)$, das sich vom Sendespektrum $S(f)$ aufgrund von Dämpfung und Rauschen zumindest geringfügig unterscheidet, kommt man zur Spektralfunktion $V(f) ≈ Q(f)$.