Modulationsverfahren/Weitere AM–Varianten: Unterschied zwischen den Versionen
| Zeile 36: | Zeile 36: | ||
{{end}} | {{end}} | ||
| + | |||
| + | ==Quadratur–Amplitudenmodulation== | ||
| + | Durch Ausnutzung der Orthogonalität von Cosinus– und Sinusfunktion kann ein Kanal zur gleichzeitigen Übertragung zweier Quellensignale $q_1(t)$ und $q_2(t)$ ohne gegenseitige Beeinträchtigungen doppelt genutzt werden. Man bezeichnet dieses Verfahren als Quadratur–Amplitudenmodulation (QAM). | ||
| + | |||
| + | |||
| + | [[Datei:P_ID1053__Mod_T_2_5_S2_neu.png | Quadratur–Amplitudenmodulation]] | ||
| + | |||
| + | |||
| + | Dieses System weist folgende Eigenschaften auf: | ||
| + | *Das Sendesignal setzt sich aus zwei zueinander orthogonalen Anteilen zusammen: | ||
| + | $$s(t) = q_1(t) \cdot \cos (\omega_{\rm T}\cdot t) - q_2(t) \cdot \sin (\omega_{\rm T}\cdot t)\hspace{0.05cm}.$$ | ||
| + | *Unter der Voraussetzung von frequenz– und phasensynchroner Demodulation lautet das Signal im oberen Zweig vor dem Tiefpass $H_{\rm E1}(f)$: | ||
| + | $$\begin{align*}b_1(t) & = q_1(t) \cdot 2 \cdot \cos^2 (\omega_{\rm T}\cdot t) - q_2(t) \cdot 2 \cdot | ||
| + | \cos (\omega_{\rm T}\cdot t)\cdot \sin (\omega_{\rm T}\cdot t)= \\ | ||
| + | & = q_1(t)\cdot \left[ 1 + \cos (2 \omega_{\rm T}\cdot t) \right] - q_2(t)\cdot \sin (2 \omega_{\rm T}\cdot t) \hspace{0.05cm}.\end{align*}$$ | ||
| + | *Durch Begrenzung auf Frequenzen $|f| < f_{\rm T}$ ergibt sich somit im oberen bzw. unteren Zweig: | ||
| + | $$v_1(t) = q_1(t),\hspace{0.3cm} v_2(t) = q_2(t)\hspace{0.05cm}.$$ | ||
| + | *Bei einem Phasenversatz $Δ{\mathbf ϕ}_{\rm T}$ zwischen den sende– und empfängerseitigen Trägersignalen kommt es neben einer Dämpfung des gewünschten Teilnehmers zusätzlich zu Übersprechen des zweiten Teilnehmers und damit zu nichtlinearen Verzerrungen: | ||
| + | $$v_1(t) = \alpha_{11} \cdot q_1(t)+ \alpha_{12} \cdot q_2(t) \hspace{0.05cm}, \hspace{0.3cm} v_2(t) = \alpha_{21} \cdot q_1(t)+ \alpha_{22} \cdot q_2(t)$$ | ||
| + | $$\Rightarrow\hspace{0.3cm}\alpha_{11} = \alpha_{22} = \cos(\Delta \phi_{\rm T}) \hspace{0.05cm}, \hspace{0.3cm} \alpha_{12} = -\alpha_{21} = \sin(\Delta \phi_{\rm T}) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
Version vom 18. Juni 2016, 19:20 Uhr
Inhaltsverzeichnis
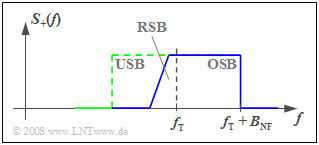
Restseitenband–Amplitudenmodulation (1)
Bei der Signalübertragung mittels Einseitenbandmodulation (ESB–AM) treten folgende Probleme auf:
- Zum Unterdrücken des unerwünschten Seitenbandes – zum Beispiel des unteren – muss ein Filter mit sehr hoher Flankensteilheit verwendet werden.
- Solche steilflankigen Filter weisen jedoch starke Gruppenlaufzeitverzerrungen auf, insbesondere an der Grenze des Durchlassbereichs.
Das Problem kann stark abgeschwächt werden, wenn man anstelle der Einseitenband–AM die Restseitenband–Amplitudenmodulation nutzt, wie in der nebenstehenden Grafik gezeigt.
Die vorliegende Beschreibung basiert auf dem Lehrbuch [Mäu88][1]. Danach kann die RSB–AM stichpunktartig wie folgt charakterisiert werden:
- Man nutzt noch einen gewissen Frequenzbereich des eigentlich unterdrückten Seitenbandes – im betrachteten Beispiel des USB – mit relativ flach abfallender Übertragungsfunktion zusätzlich aus.
- Empfängerseitig wird im Übergangsbereich vom unterdrückten zum übertragenen Seitenband eine frequenz–linear ansteigende Selektionskurve mit so genannter Nyquist–Flanke verwendet.
- Die Demodulation führt eine Faltung der Seitenbänder um den Träger durch, so dass resultierend der Nachrichteninhalt eines Bandes mit für alle Frequenzen gleicher Amplitude gewonnen wird.
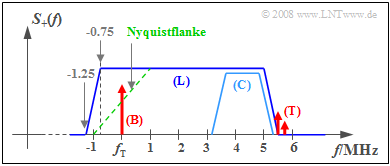
Restseitenband–Amplitudenmodulation (2)
Anwendung findet das Restseitenbandverfahren beim (analogen) Farbfernsehen, dessen Frequenzspektrum nach der CCIR–Norm in der Grafik abgebildet ist. Die angegebenen Frequenzen beziehen sich auf das in Deutschland verwendete PAL–B/G–Fernsehformat.
Man erkennt aus dieser schematischen Darstellung:
- Das abgestrahlte Spektrum (nur positive Frequenzen gezeichnet) reicht von $f_{\rm T}$ –1.25 MHz bis $f_{\rm T}$ + 5.75 MHz. Das untere Restseitenband ist inklusive der Nyquistflanke ca. 1.25 MHz breit.
- Die grün-gestrichelte Linie zeigt die Empfänger–Durchlasskurve. Der Bildträger (B) bei der Trägerfrequenz $f_{\rm T}$ liegt mittig zu dieser Nyquistflanke.
- Das Luminanzsignal (L) geht bis etwa 5 MHz. Es enthält die Information für die Bildhelligkeit und die Farbe „Grün”.
- Im oberen Teil ist das Chromianzsignal (C) eingebettet. Dabei werden zwei orthogonale Träger bei 4.43 MHz für „Rot” und „Blau” QAM–moduliert; der Träger wird dabei unterdrückt.
- Der Tonträger (T) liegt bei $f_{\rm T}$ + 5.5 MHz und ist um 12 dB niedriger als der Bildträger. Falls eine Stereo– oder Zweikanaltonübertragung vorliegt, folgt bei 5.75 MHz ein zweiter Tonträger.
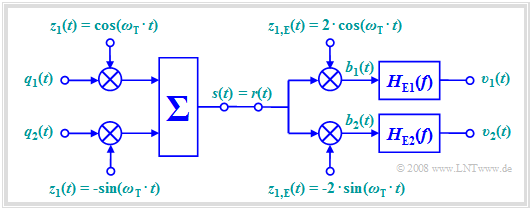
Quadratur–Amplitudenmodulation
Durch Ausnutzung der Orthogonalität von Cosinus– und Sinusfunktion kann ein Kanal zur gleichzeitigen Übertragung zweier Quellensignale $q_1(t)$ und $q_2(t)$ ohne gegenseitige Beeinträchtigungen doppelt genutzt werden. Man bezeichnet dieses Verfahren als Quadratur–Amplitudenmodulation (QAM).
Dieses System weist folgende Eigenschaften auf:
- Das Sendesignal setzt sich aus zwei zueinander orthogonalen Anteilen zusammen:
$$s(t) = q_1(t) \cdot \cos (\omega_{\rm T}\cdot t) - q_2(t) \cdot \sin (\omega_{\rm T}\cdot t)\hspace{0.05cm}.$$
- Unter der Voraussetzung von frequenz– und phasensynchroner Demodulation lautet das Signal im oberen Zweig vor dem Tiefpass $H_{\rm E1}(f)$:
$$\begin{align*}b_1(t) & = q_1(t) \cdot 2 \cdot \cos^2 (\omega_{\rm T}\cdot t) - q_2(t) \cdot 2 \cdot \cos (\omega_{\rm T}\cdot t)\cdot \sin (\omega_{\rm T}\cdot t)= \\ & = q_1(t)\cdot \left[ 1 + \cos (2 \omega_{\rm T}\cdot t) \right] - q_2(t)\cdot \sin (2 \omega_{\rm T}\cdot t) \hspace{0.05cm}.\end{align*}$$
- Durch Begrenzung auf Frequenzen $|f| < f_{\rm T}$ ergibt sich somit im oberen bzw. unteren Zweig:
$$v_1(t) = q_1(t),\hspace{0.3cm} v_2(t) = q_2(t)\hspace{0.05cm}.$$
- Bei einem Phasenversatz $Δ{\mathbf ϕ}_{\rm T}$ zwischen den sende– und empfängerseitigen Trägersignalen kommt es neben einer Dämpfung des gewünschten Teilnehmers zusätzlich zu Übersprechen des zweiten Teilnehmers und damit zu nichtlinearen Verzerrungen:
$$v_1(t) = \alpha_{11} \cdot q_1(t)+ \alpha_{12} \cdot q_2(t) \hspace{0.05cm}, \hspace{0.3cm} v_2(t) = \alpha_{21} \cdot q_1(t)+ \alpha_{22} \cdot q_2(t)$$ $$\Rightarrow\hspace{0.3cm}\alpha_{11} = \alpha_{22} = \cos(\Delta \phi_{\rm T}) \hspace{0.05cm}, \hspace{0.3cm} \alpha_{12} = -\alpha_{21} = \sin(\Delta \phi_{\rm T}) \hspace{0.05cm}.$$
Quellenverzeichnis
- ↑ Mäusl, R.: Analoge Modulationsverfahren. Heidelberg: Dr. Hüthig, 1988.