Modulationsverfahren/Frequenzmodulation (FM): Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
$$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) | $$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet $K_{\rm FM} eine dimensionsbehaftete Konstante. Beschreibt $q(t)$ einen Spannungsverlauf, so hat $K_{\rm FM}$ die Einheit $\rm V^{–1}s^{–1}$. | + | Hierbei bezeichnet $K_{\rm FM}$ eine dimensionsbehaftete Konstante. Beschreibt $q(t)$ einen Spannungsverlauf, so hat $K_{\rm FM}$ die Einheit $\rm V^{–1}s^{–1}$. |
{{end}} | {{end}} | ||
| Zeile 67: | Zeile 67: | ||
Aus dieser Gleichung lässt sich sofort ablesen: | Aus dieser Gleichung lässt sich sofort ablesen: | ||
| − | *Auch bei der Frequenzmodulation bewegt sich das äquivalente TP–Signal wegen der konstanten Hüllkurve ⇒ a(t) = | + | *Auch bei der Frequenzmodulation bewegt sich das äquivalente TP–Signal wegen der konstanten Hüllkurve ⇒ $a(t) = A_{\rm T}$ auf einem Kreisbogen. |
| − | + | *Ein Frequenzmodulator kann mit Hilfe eines Integrators und eines Phasenmodulators realisiert werden. Der FM–Demodulator besteht demzufolge aus PM–Demodulator und Differenzierer. | |
| − | |||
| − | |||
Version vom 19. Juni 2016, 15:09 Uhr
Augenblicksfrequenz (1)
Wir gehen wieder von einem winkelmodulierten Signal aus: $$s(t) = A_{\rm T} \cdot \cos (\psi(t)).$$ Alle Informationen über das Quellensignal $q(t)$ sind damit ausschließlich in der Winkelfunktion $ψ(t)$ enthalten, während die Hüllkurve $a(t) = A_{\rm T}$ konstant ist.
Die Augenblickskreisfrequenz ist die Ableitung der Winkelfunktion nach der Zeit: $$\omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}\hspace{0.05cm}.$$ Entsprechend gilt für die Augenblicksfrequenz: $$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi} = \frac{1}{2\pi} \cdot \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}\hspace{0.05cm}.$$
Bei einer Winkelmodulation mit der Trägerfrequenz $f_{\rm T}$ schwankt die Augenblicksfrequenz zwischen
$$f_{\rm T} - \Delta f_{\rm A} \le f_{\rm A}(t) \le f_{\rm T} + \Delta f_{\rm A}\hspace{0.05cm}.$$
Dabei bezeichnet man die maximale Abweichung $Δf_{\rm A}$ der zeitabhängigen Augenblicksfrequenz $f_{\rm A}(t)$ von der konstanten Trägerfrequenz fT als den Frequenzhub.
Hervorzuheben ist, dass ein grundsätzlicher Unterschied zwischen der Augenblicksfrequenz und dem mit einem Spektrum–Analyzer messbaren Spektrum eines winkelmodulierten Signals besteht, wie das nachfolgende Beispiel verdeutlichen soll.
Augenblicksfrequenz (2)
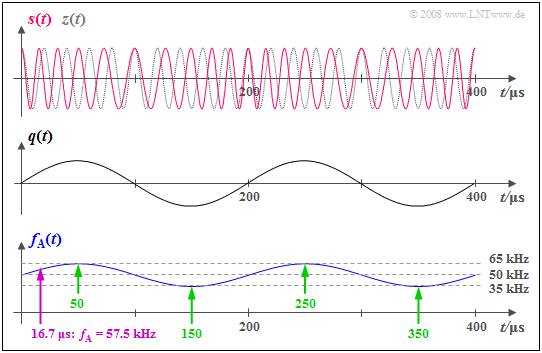
Die Grafik zeigt oben das phasenmodulierte Signal $$s(t) = A_{\rm T} \cdot \cos (\psi(t)) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} \hspace{0.05cm}t + \eta \cdot \sin (2 \pi f_{\rm N} \hspace{0.05cm} t))$$
sowie unten die Augenblicksfrequenz
$$f_{\rm A}(t) = \frac{1}{2 \pi} \cdot \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t} = f_{\rm T} + \Delta f_{\rm A}\cdot \cos (2 \pi f_{\rm N} \hspace{0.05cm} t) \hspace{0.05cm}.$$
Die zugrundeliegenden Systemparameter sind $f_{\rm T} =$ 50 kHz, $f_{\rm N} =$ 5 kHz und $η =$ 3. Daraus ergibt sich der Frequenzhub zu $Δf_{\rm A} = η · f_{\rm N} =$ 15 kHz.
In der Mitte ist zur Orientierung der qualitative Verlauf des sinusförmigen Quellensignals $q(t)$ skizziert. Man erkennt aus diesen Grafiken:
- Die Augenblicksfrequenz $f_{\rm A}(t)$ kann alle beliebigen Werte zwischen $f_{\rm T} + Δf_{\rm A} =$ 65 kHz (bei $t =$ 50, 250 μs, usw.) und $f_{\rm T} \ – Δf_{\rm A} =$ 35 kHz (bei $t =$ 150, 350 μs, usw.) annehmen (siehe grüne Markierungen). Zur Zeit $t ≈$ 16.7 μs gilt beispielsweise $f_{\rm A}(t) =$ 57.5 kHz (violetter Pfeil).
- Dagegen besteht die Spektralfunktion $S(f)$ aus diskreten Bessellinien bei den Frequenzen . . . , 30, 35, 40, 45, 50, 55, 60, 65, 70, ... (jeweils in kHz). Eine Spektrallinie bei $f =$ 57.5 kHz gibt es nicht im Gegensatz zu einer Spektrallinie bei $f =$ 70 kHz. Dagegen gilt zu keinem Zeitpunkt $f_{\rm A}(t) =$ 70 kHz.
Ergo: Die Augenblicksfrequenz $f_{\rm A}(t)$ ist also keine physikalisch messbare Frequenz im herkömmlichen Sinne, sondern nur eine fiktive, mathematische Größe, nämlich die Ableitung der Winkelfunktion $ψ(t)$.
Signalverläufe bei Frequenzmodulation
Wie in Kapitel 3.1 gehen wir weiterhin davon aus, dass das Trägersignal $z(t)$ cosinusförmig verläuft und das Quellensignal $q(t)$ spitzenwertbegrenzt ist.
Ist bei einem Übertragungssystem die Augenblickskreisfrequenz $ω_{\rm A}(t)$ linear abhängig vom Momentanwert des Quellensignals $q(t)$, so spricht man von Frequenzmodulation (FM): $$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$ Hierbei bezeichnet $K_{\rm FM}$ eine dimensionsbehaftete Konstante. Beschreibt $q(t)$ einen Spannungsverlauf, so hat $K_{\rm FM}$ die Einheit $\rm V^{–1}s^{–1}$.
Für die Winkelfunktion und das modulierte Signal erhält man bei FM:
$$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm}{\rm d}t \hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \cos (\psi(t)) \hspace{0.05cm}.$$
Aus dieser Gleichung lässt sich sofort ablesen:
- Auch bei der Frequenzmodulation bewegt sich das äquivalente TP–Signal wegen der konstanten Hüllkurve ⇒ $a(t) = A_{\rm T}$ auf einem Kreisbogen.
- Ein Frequenzmodulator kann mit Hilfe eines Integrators und eines Phasenmodulators realisiert werden. Der FM–Demodulator besteht demzufolge aus PM–Demodulator und Differenzierer.
Die untere Abbildung zeigt den umgekehrten Zusammenhang, nämlich die mögliche Beschreibung von PM–Modulator und –Demodulator durch die entsprechenden FM–Komponenten.