Aufgaben:Aufgabe 1.2Z: Messung der Übertragungsfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Frequenzbereich}} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {M…“) |
|||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Frequenzbereich}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Frequenzbereich}} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID788__LZI_Z_1_2.png |right|Gemessene Signalamplituden und Phasen bei Filter B (Aufgabe Z1.2)]] |
| + | Zur messtechnischen Bestimmung des Frequenzgangs von Filtern wird ein sinusförmiges Eingangssignal mit der Amplitude 2 V und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt. | ||
| + | |||
| + | Das Betragsspektrum am Ausgang von Filter A lautet mit der Frequenz $f_0 =$ 1 kHz: | ||
| + | $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f | ||
| + | \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ | ||
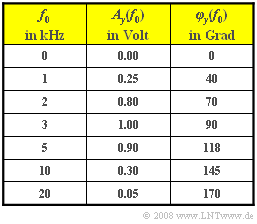
| + | Bei einem anderen Filter B ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt: | ||
| + | $$Y_{\rm B} (f) = \frac{A_y}{2} \cdot {\rm e}^{ {\rm j} \varphi_y} | ||
| + | \cdot {\rm \delta } (f + f_0) + \frac{A_y}{2} \cdot {\rm e}^{ | ||
| + | -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$ | ||
| + | Das Filter B soll in der Aufgabe in der Form | ||
| + | $$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} | ||
| + | \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}$$ | ||
| + | |||
| + | dargestellt werden; $a_{\rm B}(f)$ wird als Dämpfungsverlauf und $b_{\rm B}(f)$ als Phasenverlauf bezeichnet. | ||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [[Systembeschreibung_im_Frequenzbereich | Kapitel 1.1]]. | ||
Version vom 9. Juli 2016, 16:14 Uhr
Zur messtechnischen Bestimmung des Frequenzgangs von Filtern wird ein sinusförmiges Eingangssignal mit der Amplitude 2 V und vorgegebener Frequenz $f_0$ angelegt. Das Ausgangssignal $y(t)$ bzw. dessen Spektrum $Y(f)$ werden dann nach Betrag und Phase ermittelt.
Das Betragsspektrum am Ausgang von Filter A lautet mit der Frequenz $f_0 =$ 1 kHz: $$|Y_{\rm A} (f)| = 1.6\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm f_0) + 0.4\hspace{0.05cm}{\rm V} \cdot {\rm \delta } (f \pm 3 f_0) .$$ Bei einem anderen Filter B ist das Ausgangssignal dagegen stets eine harmonische Schwingung mit der (einzigen) Frequenz $f_0$. Bei den in der Tabelle angegebenen Frequenzen $f_0$ werden die Amplituden $A_y(f_0)$ und die Phasen $φ_y(f_0)$ gemessen. Hierbei gilt: $$Y_{\rm B} (f) = \frac{A_y}{2} \cdot {\rm e}^{ {\rm j} \varphi_y} \cdot {\rm \delta } (f + f_0) + \frac{A_y}{2} \cdot {\rm e}^{ -{\rm j} \varphi_y} \cdot {\rm \delta } (f - f_0).$$ Das Filter B soll in der Aufgabe in der Form $$H_{\rm B}(f) = {\rm e}^{-a_{\rm B}(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_{\rm B}(f)}$$
dargestellt werden; $a_{\rm B}(f)$ wird als Dämpfungsverlauf und $b_{\rm B}(f)$ als Phasenverlauf bezeichnet.
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.1.
Fragebogen
Musterlösung
- a)
- b)
- c)
- d)
- e)
- f)
- g)