Aufgaben:Aufgabe 1.3Z: Exponentiell abfallende Impulsantwort

• Zurück zum Buch

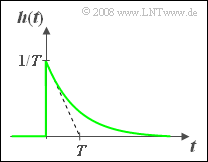
Gemessen wurde die Impulsantwort $h(t)$ eines LZI–Systems, die für alle Zeiten $t$ < 0 identisch 0 ist und für $t$ > 0 entsprechend einer Exponentialfunktion abfällt: $$h(t) = \frac{1}{T} \cdot {\rm e}^{-t/T}.$$ Der Funktionsparameter sei $T =$ 1 ms. In der Teilaufgabe 3) ist nach der 3dB–Grenzfrequenz $f_{\rm G}$ gefragt, die wie folgt implizit definiert ist: $$|H(f = f_{\rm G})| = \frac{1}{\sqrt{2}} \cdot|H(f = 0)| .$$ Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.2. Gegeben ist das folgende bestimmte Integral: $$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = \frac{\pi}{2} .$$

Fragebogen

1

Berechnen Sie den Frequenzgang $H(f)$. Welcher Wert ergibt sich für $f =$ 0?

$H(f = 0) =$

2

Welchen Wert besitzt die Impulsantwort zur Zeit $t =$ 0?

$h(t = 0) =$ 1/s

3

Berechnen Sie die 3dB–Grenzfrequenz $f_{\rm G}$.

$f_{\rm G} =$ Hz

4

Welche der nachfolgenden Aussagen sind zutreffend?

	Das betrachtete System ist kausal.
	Das betrachtete System hat Hochpass–Charakter.
	Liegt am Systemeingang ein Cosinussignal der Frequenz $f_{\rm G}$ an, so ist das Ausgangssignal ebenfalls cosinusförmig.

Musterlösung

Musterlösung

1. Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$: $$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} {\rm d}t.$$ Die Integration führt zum Ergebnis: $$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$ Bei der Frequenz $f =$ 0 hat der Frequenzgang $\rm \underline{\: den \: Wert \: 1}$. 2. 3. 4. 5. 6. 7.