Aufgaben:Aufgabe 1.5: Idealer rechteckförmiger Tiefpass

• Zurück zum Buch

Wir betrachten einen idealen, rechteckförmigen Tiefpass – manchmal auch Küpfmüller–Tiefpass genannt, der

• alle Frequenzen $f <$ 5 kHz unverfälscht durchlässt ⇒ $H(f) = 1$,
• alle Spektralanteile über 5 kHz vollständig unterdrückt ⇒ $H(f) = 0$.

Exakt bei der Grenzfrequenz $f_{\rm G} =$ 5 kHz ist der Wert der Übertragungsfunktion gleich 1/2.

An den Eingang des Tiefpasses werden verschiedene Signale angelegt:

• ein schmaler Rechteckimpuls geeigneter Höhe, der durch einen Diracimpuls angenähert werden kann:

$$x_1(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot {\rm \delta}(t),$$

• ein Diracpuls im Zeitabstand $T_{\rm A}$:

$$x_2(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot \sum_{\nu = -\infty}^{+\infty}{\rm \delta}(t - \nu \cdot T_{\rm A}),$$

wobei das zugehörige Spektrum mit $f_{\rm A} = 1/T_{\rm A}$ lautet:

$$X_2(f) = \frac{10^{-3}\hspace{0.1cm}{\rm Vs}}{T_{\rm A}} \cdot\sum_{\mu = -\infty}^{+\infty}{\rm \delta}(f - \mu \cdot f_{\rm A}),$$

• eine Sprungfunktion zum Zeitpunkt $t = 0$:

$$x_3(t) = 10\hspace{0.1cm}{\rm V} \cdot \gamma(t) = \left\{ \begin{array}{c} 0 \\ 5\hspace{0.1cm}{\rm V} \\ 10\hspace{0.1cm}{\rm V} \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ t < 0,} \\{ t = 0,} \\ { t > 0,} \\ \end{array}$$

• ein si–förmiger Impuls mit der äquivalenten Dauer $T$:

$$x_4(t) = 10\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \cdot {t}/{T}) .$$

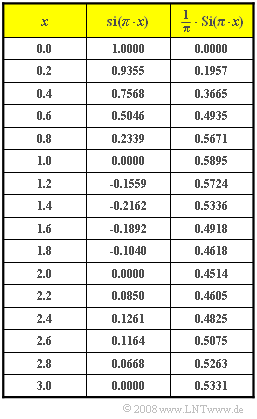
Hinweis: Die Aufgabe bezieht sich auf die Beschreibungen von Kapitel 1.3. In der Tabelle sind die Funktionswerte der Spaltfunktion ${\rm si}(πx)$ und der Integralsinusfunktion ${\rm Si}(πx)$ aufgelistet: $${\rm Si}(\pi x) = \int_{ 0 }^{ x } {{\rm si} ( \pi \xi )} \hspace{0.1cm}{\rm d}\xi .$$

Fragebogen

1

Welches Ausgangssignal $y_1(t)$ ergibt sich als Antwort auf den Diracimpuls $x_1(t)$, insbesondere zu den Zeitpunkten $t =$ 0 und $t =$ 50 μs?

$y_1(t = 0) =$ V

$y_1(t = 50 {\: \rm \mu s}) =$ V

2

Wie lautet das Ausgangssignal $y_2(t)$, wenn am Filtereingang der Diracpuls $x_2(t)$ anliegt und $T_{\rm A} =$ 200 μs gilt. Welcher Signalwert tritt bei $t =$ 0 auf?

$T_{\rm A} = {\rm 200 μs} : y_2(t = 0) =$ V

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.