Aufgaben:Aufgabe 1.1Z: Summe zweier Ternärsignale: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Mengentheoretische Grundlagen}} right| Gegeben seien zwei dreistufige Nac…“) |
Nabil (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Stochastische Signaltheorie/ | + | {{quiz-Header|Buchseite=Stochastische Signaltheorie/Einige grundlegende Definitionen}} |
[[Datei:P_ID146__Sto_Z1_1.png|right|]] | [[Datei:P_ID146__Sto_Z1_1.png|right|]] | ||
| Zeile 47: | Zeile 47: | ||
| − | [[Category:Aufgaben zu Stochastische Signaltheorie|^1. | + | [[Category:Aufgaben zu Stochastische Signaltheorie|^1.1 Einige grundlegende Definitionen |
| + | ^]] | ||
Version vom 28. August 2016, 20:07 Uhr
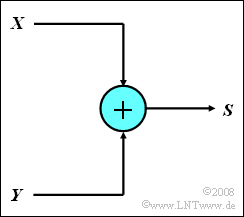
Gegeben seien zwei dreistufige Nachrichtenquellen $X$ und $Y$, deren Ausgangssignale jeweils nur die Werte –1, 0 und +1 annehmen können. Die Signalquellen sind statistisch voneinander unabhängig. Eine einfache Schaltung bildet nun das Summensignal $S = X + Y$. Bei der Signalquelle $X$ treten die Werte –1, 0 und +1 mit gleicher Wahrscheinlichkeit auf, während bei der Quelle $Y$ der Signalwert 0 doppelt so wahrscheinlich ist wie die beiden anderen Werte –1 bzw. +1.
Hinweis: Diese Aufgabe bezieht sich auf den gesamten Stoff von Kapitel 1.1. Der Inhalt dieses Abschnitts ist im nachfolgenden Lernvideo zusammengefasst:
Fragebogen
Musterlösung
- a)
- b)
- c)
- d)
- e)
- f)
- g)