Aufgaben:Aufgabe 4.8Z: AWGN-Kanal: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) |
Nabil (Diskussion | Beiträge) K (Nabil verschob die Seite Zusatzaufgaben:4.8 AWGN-Kanal nach 4.8Z AWGN-Kanal) |
Version vom 13. Oktober 2016, 20:21 Uhr
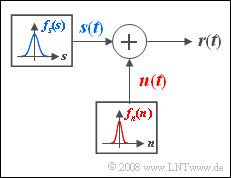
- Wir betrachten hier ein analoges Nachrichtensignal $s(t)$, dessen Amplitudenwerte gaußverteilt sind. Der Effektivwert $\sigma_s$ dieses mittelwertfreien Signals beträgt 1 V. Diese Größe bezeichnet man auch als die Streuung.
- Bei der Übertragung wird $s(t)$ von einem Störsignal $n(t)$ additiv überlagert, das ebenso wie $s(t)$ als gaußverteilt und mittelwertfrei angenommen werden kann. Der Effektivwert (die Streuung) des Störsignals sei allgemein $\sigma_n$. Es kann angenommen werden, dass zwischen Nutzsignal $s(t)$ und Störsignal $n(t)$ keine statistischen Abhängigkeiten bestehen.
- Man bezeichnet eine solche Konstellation als Additive White Gaussian Noise (AWGN) und verwendet als Qualitätskriterium für das Empfangssignal $r(t)$ das Signal-zu-Störverhältnis (Signal-to-Noise-Ratio):
- $${\rm SNR} = \frac {\sigma_s^2}{\sigma_n^2}.$$
- Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2 und Kapitel 4.3.
Fragebogen
Musterlösung
- 1. Es gilt r(t) = s(t) + n(t). Somit kann fr(r) aus der Faltung der beiden Dichtefunktionen fs(s) und fn(n) berechnet werden. Da beide Signale gaußverteilt sind, liefert die Faltung ebenfalls eine Gaußfunktion:
- $$f_r(r)= \frac {1}{\sqrt{2 \pi} \cdot \sigma_r} \cdot {\rm e}^{-r^2/(2 \sigma_r^2)}.$$
- Die Varianzen von s(t) und n(t) addieren sich. Deshalb erhält man mit σs = 1 V und σn = 0.75 V:
- $$\sigma_r = \sqrt{\sigma_s^2 + \sigma_n^2} =\sqrt{{(\rm 1\hspace{0.1cm}V)^2} + {(\rm 0.75\hspace{0.1cm}V)^2}}\hspace{0.15cm}\underline{ = {\rm 1.25\hspace{0.1cm}V}}.$$
- 2. Für den Korrelationskoeffizienten gilt mit dem gemeinsamen Moment msr:
- $$\rho_{sr } = \frac{m_{sr }}{\sigma_s \cdot \sigma_r}.$$
- Hierbei ist berücksichtigt, dass s(t) und auch r(t) mittelwertfrei sind, so dass μsr = msr gilt. Da s(t) und n(t) als statistisch unabhängig voneinander – und damit unkorreliert – vorausgesetzt wurden, gilt weiter:
- $$m_{sr} = {\rm E}[s(t) \cdot r(t)] = {\rm E}[s^2(t)] + {\rm E}[s(t) \cdot n(t)] ={\rm E}[s^2(t)] = \sigma_s^2.$$
- Daraus folgt:
- $$\rho_{sr } = \frac{\sigma_s}{ \sigma_r} = \sqrt{\frac{\sigma_s^2}{\sigma_s^2 + \sigma_n^2}} = \left (1+ \frac{\sigma_n^2}{\sigma_s^2}\right)^{-1/2}.$$
- Mit σs = 1 V, σn = 0.75 V und σr = 1.25 V erhält man ρsr = 0.8.
- 3. Der in b) berechnete Ausdruck kann mit der Abkürzung SNR = σs2/σn2 wie folgt dargestellt werden:
- $$\rho_{sr } = \frac{1}{ \sqrt{1 + \frac{1}{SNR}}} \approx \frac{1}{ {1 + \frac{1}{2 \cdot SNR}}} \approx 1 - \frac{1}{2 \cdot SNR}.$$
- Der Signal-zu-Stör-Abstand 10 · lg(SNR) = 30 dB führt zum absoluten Wert SNR = 1000. In die obige Gleichung eingesetzt ergibt dies näherungsweise einen Korrelationskoeffizienten von 0.9995.