Aufgaben:Aufgabe 3.2Z: 2D–Wahrscheinlichkeitsfunktion

• Zurück zum Buch

Wir betrachten die Zufallsgrößen

$X$ = { 0, 1, 2, 3 },

$Y$ = { 0, 1, 2 },

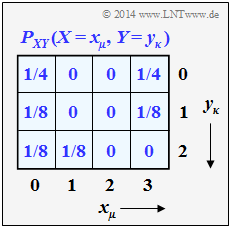
deren gemeinsame Wahrscheinlichkeitsfunktion $P_{X,Y}(X,Y)$ gegeben ist. Aus dieser 2D–Wahrscheinlichkeitsfunktion sollen die eindimensionalen Wahrscheinlichkeitsfunktionen $P_X(X)$ und $P_Y(Y)$ ermittelt werden. Man nennt eine solche manchmal auch Randwahrscheinlichkeit (englisch: Marginal Probability).

Gilt $P_{X,Y}(X,Y)$ = $P_X(X)$ . $P_Y(Y)$, so sind die beiden Zufallsgrößen X und Y statistisch unabhängig. Andernfalls bestehen statistische Bindungen zwischen $X$ und $Y$.

Im zweiten Teil der Aufgabe betrachten wir die Zufallsgrößen

$U$ = { 0, 1 }, $V$ = { 0, 1 },

die sich aus $X$ und $Y$ durch Modulo–2–Operationen ergeben:

$U$ = $X$ mod 2, $V$ = $Y$ mod 2.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 3.1 .Ausgegangen wird hier von der gleichen Konstellation wie in

Fragebogen

1

Multiple-Choice Frage

	Falsch
	Richtig

2

Input-Box Frage

$\alpha$ =

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.