Aufgaben:Aufgabe 3.7: Einige Entropieberechnungen: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 35: | Zeile 35: | ||
| + | ===Fragebogen=== | ||
| + | |||
| + | <quiz display=simple> | ||
| − | == | + | {Berechnen Sie die Verbundentropie. |
| + | |type="{}"} | ||
| + | $H(XY)$ = { 1.393 3% } $bit$ | ||
| − | + | {Welche Entropien weisen die 1D–Zufallsgrößen $X$ und $Y$ auf? | |
| − | { | + | |type="{}"} |
| − | |type=" | + | $H(X)$ = { 0.722 3% } $bit$ |
| − | + | $H(Y)$ = { 0.925 3% } $bit$ | |
| − | |||
| + | {Wie groß ist die Transinformation zwischen den Zufallsgrößen $X$ und $Y$? | ||
| + | |type="{}"} | ||
| + | $I(X; Y)$ = { 0.254 3% } $bit$ | ||
| − | { | + | {Berechnen Sie die beiden bedingten Entropien. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H(X|Y)$ = { 0.468 3% } $bit$ |
| + | $H(Y|X)$ = { 0.671 3% } $bit$ | ||
| + | |||
| + | {Welche der folgenden Aussagen treffen für die 2D–Zufallsgröße $UV$ zu? | ||
| + | |type="[]"} | ||
| + | + Die 1D–Zufallsgrößen $U$ und $V$ sind statistisch unabhängig. | ||
| + | + Die gemeinsame Information von $U$ und $V \Rightarrow I(U; V)$ ist $0$. | ||
| + | - Für die Verbundentropie gilt $H(UV) = H(XY)$. | ||
| + | + Es gelten die Beziehungen $H(U|V) = H(U) und H(V|U) = H(V)$. | ||
Version vom 26. November 2016, 15:41 Uhr
Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen:
$$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$
$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$
Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden:
- die Verbundentropie (englisch: Joint Entropy):
$H(XY) = -E[log_2 P_{ XY }( X,Y)]$
- die beiden Einzelentropien:
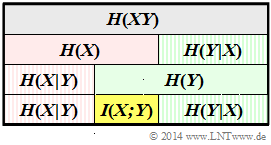
$$H(X) = -E[log_2 P_X( X)]$$ $$H(Y) = -E[log_2 P_Y( Y)]$$ Daraus lassen sich entsprechend dem obigen Schema – dargestellt für die Zufallsgröße $XY$ – noch die folgenden Beschreibungsgrößen sehr einfach bestimmen:
- die bedingten Entropien (englisch: Conditional Entropies):
$H(X \mid Y) = -E[log_2 P_{ X \mid Y }( X \mid Y)]$
$H(Y \mid Y) = -E[log_2 P_{ Y \mid X }( Y \mid X)]$
- die Transinformation (englisch: Mutual Information) zwischen $X$ und $Y$:
$I(X;Y) = E [log_2 \frac{P_{ XY }(X,Y)}{P_X(X) . P_Y(Y)}]$
Abschließend sind qualitative Aussagen hinsichtlich der zweiten Zufallsgröße $UV$ zu verifizieren. Hinwies: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 3.2.
Fragebogen
Musterlösung