Aufgaben:Aufgabe 3.10Z: BSC–Kanalkapazität: Unterschied zwischen den Versionen

Version vom 27. November 2016, 22:22 Uhr

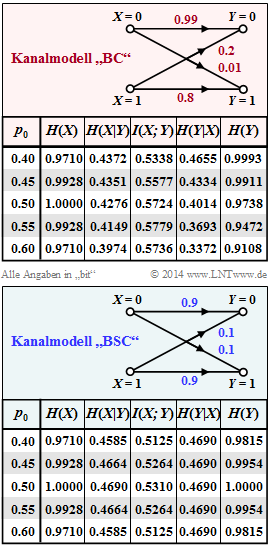
Die Kanalkapazität $C$ wurde von Claude $E$. Shannon als die maximale Transinformation definiert, wobei sich die Maximierung allein auf die Quellenstatistik bezieh $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ Beim Binärkanal mit der Wahrscheinlichkeitsfunktion $P_X(X) = [p_0, p:1]$ ist nur ein Parameter optimierbar, beispielsweise $p_0$. Die Wahrscheinlichkeit für eine $„1”$ ist damit ebenfalls festgelegt: $p_1 = 1 – p_0$

Die obere Grafik (rot hinterlegt) fasst die Ergebnisse für den unsymmetrischen Binärkanal mit $ε_0 = 0.01$ und $ε_1 = 0.2$ zusammen, der im Theorieteil betrachtet wurde. Die Maximierung führt zum Ergebnis $p_0 = 0.55$

$\Rightarrow p_1 = 0.45$, und man erhält für die Kanalkapazität: $$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}$$

In der unteren Grafik (blaue Hinterlegung) sind die gleichen informationstheoretischen Größen für den symmetrischen Kanal $\Rightarrow$ Binary Symmetric Channel (BSC) mit den Verfälschungswahrscheinlichkeiten $ε1 = ε2 = ε = 0.1$ angegeben, der auch für die Aufgabe A3.9 vorausgesetzt wurde.

In der vorliegenden Aufgabe sollen Sie für das BSC–Kanalmodell (zunächst für $ε = 0\ cdot 1$)

die Entropien $H(X)$, $H(Y)$, $H(X|Y)$, $H(Y|X)$ analysieren,
den Quellenparameter $p_0$ hinsichtlich maximaler Transinformation $I(X; Y)$ optimieren,
somit die Kanalkapazität $C(ε)$ bestimmen, sowie
durch Verallgemeinerung eine geschlossene Gleichung für $C(ε)$ angeben.

Hinweis: Die Aufgabe bezieht sich auf die Thematik von Kapitel 3.3

Fragebogen

$p_0 = 0.4: H(X)$ =

$bit$

$p_0 = 0 \cdot 4: H(Y)$ =

$bit$

$p_0 = 0\cdot 4: H(XY)$ =

$bit$

$p_0 = 0\cdot 4: I(X; Y)$ =

$bit$

$ Maximierung: p_0$ =

$C$ =

$bit$

$p_0 gemäß (e): H(X|Y)$ =

$bit$

$H(Y|X)$ =

$bit$

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 15: / Zeile 15: @@
 In der unteren Grafik (blaue Hinterlegung) sind die gleichen informationstheoretischen Größen für den symmetrischen Kanal $\Rightarrow$ [http://www.lntwww.de/index.php?title=Digitalsignal%C3%BCbertragung/Binary_Symmetric_Channel_(BSC)&action=edit&redlink=1 Binary Symmetric Channel] (BSC) mit den Verfälschungswahrscheinlichkeiten $ε1 = ε2 = ε = 0.1$ angegeben, der auch für die [http://www.lntwww.de/Aufgaben:3.09_Transinformation_beim_BSC Aufgabe A3.9] vorausgesetzt wurde.
-In der vorliegenden Aufgabe sollen Sie für das BSC–Kanalmodell (zunächst für $ε = 0.1$)
+In der vorliegenden Aufgabe sollen Sie für das BSC–Kanalmodell (zunächst für $ε = 0\ cdot 1$)
 :* die Entropien $H(X)$, $H(Y)$, $H(X|Y)$, $H(Y|X)$ analysieren,
 :* den Quellenparameter $p_0$ hinsichtlich maximaler Transinformation $I(X; Y)$ optimieren,
@@ Zeile 24: / Zeile 24: @@
 <quiz display=simple>
-{Multiple-Choice Frage
-|type="[]"}
-- Falsch
-+ Richtig
+{Berechnen Sie die Quellenentropie allgemein und für $p_0 = 0.4.$
+|type="{}"}
+$p_0 = 0.4:   H(X)$ = { 0.971 3% } $bit$
-{Input-Box Frage
+{Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4.$
 |type="{}"}
-$\alpha$ = { 0.3 }
+$p_0 = 0 \cdot 4:   H(Y)$ = { 0.881 3% }  $bit$
+{Berechnen Sie die Verbundentropie allgemein und für $p_0 = 0.4.$
+|type="{}"}
+$p_0 = 0\cdot 4:   H(XY)$ = { 1.571 3% } $bit$
+{Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4.$
+|type="{}"}
+$p_0 = 0\cdot 4:   I(X; Y)$ = { 0.281 3% } $bit$
+{Welche Wahrscheinlichkeit $p_0$ führt zur Kanalkapazität $C$?
+|type="{}"}
+$ Maximierung:   p_0$ = { 0.6 3% }
+{Wie groß ist die Kanalkapazität des vorliegenden Kanals?
+|type="{}"}
+$C$ = { 0.322 3% }   $bit$
+{Wie groß sind die bedingten Entropien?
+|type="{}"}
+$p_0 gemäß (e):   H(X|Y)$ = { 0.649 3% }   $bit$
+$H(Y|X)$ = { 0.4 3% } $bit$
 </quiz>