Digitalsignalübertragung/Viterbi–Empfänger: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 41: | Zeile 41: | ||
Bei bipolarer Signalisierung ist der Algorithmus nicht aufwändiger. Dagegen steigt der Rechenaufwand, wenn der Detektionsgrundimpuls breiter wird und mehr als nur einen Vorläufer <i>g</i><sub>–1</sub> aufweist. Die Vernachlässigung von Nachläufern stellt keine grundlegende Einschränkung dar, weil jeder Impuls <i>g<sub>d</sub></i>(<i>t</i>) diese Bedingung durch geeignete Wahl des Detektionszeitpunktes <i>T</i><sub>D</sub> erfüllen kann. Anzumerken ist weiter, dass im Folgenden alle Signalwerte auf 1 normiert werden.<br> | Bei bipolarer Signalisierung ist der Algorithmus nicht aufwändiger. Dagegen steigt der Rechenaufwand, wenn der Detektionsgrundimpuls breiter wird und mehr als nur einen Vorläufer <i>g</i><sub>–1</sub> aufweist. Die Vernachlässigung von Nachläufern stellt keine grundlegende Einschränkung dar, weil jeder Impuls <i>g<sub>d</sub></i>(<i>t</i>) diese Bedingung durch geeignete Wahl des Detektionszeitpunktes <i>T</i><sub>D</sub> erfüllen kann. Anzumerken ist weiter, dass im Folgenden alle Signalwerte auf 1 normiert werden.<br> | ||
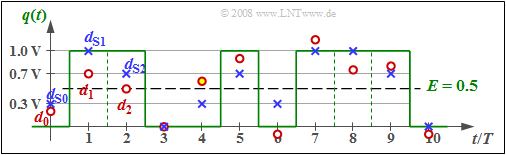
| − | {{Beispiel}}''':''' In der Grafik sind die Detektionsnutzabtastwerte <i>d<sub>sν</sub></i> als (blaue) Kreuze eingetragen, wobei die zugehörigen Amplitudenkoeffizienten <i>a</i><sub>1</sub> = 1, <i>a</i><sub>2</sub> = 1, <i>a</i><sub>3</sub> = 0, ... aus dem grün eingezeichneten Quellensignal <i>q</i>(<i>t</i>) abgelesen werden können. Die Grundimpulswerte sind in diesem Beispiel zu | + | {{Beispiel}}''':''' In der Grafik sind die Detektionsnutzabtastwerte <i>d<sub>sν</sub></i> als (blaue) Kreuze eingetragen, wobei die zugehörigen Amplitudenkoeffizienten <i>a</i><sub>1</sub> = 1, <i>a</i><sub>2</sub> = 1, <i>a</i><sub>3</sub> = 0, ... aus dem grün eingezeichneten Quellensignal <i>q</i>(<i>t</i>) abgelesen werden können. Die Grundimpulswerte sind in diesem Beispiel zu <i>g</i><sub>0</sub> = 0.7 und <i>g</i><sub>–1</sub> = 0.3 angenommen. Aus der Grafik ist weiter zu erkennen, dass <i>d</i><sub>S<i>ν</i></sub> nur vier verschiedene Werte, nämlich 0, <i>g</i><sub>0</sub>, <i>g</i><sub>–1</sub> und |
<i>g</i><sub>0</sub> + <i>g</i><sub>–1</sub>, annehmen kann.<br> | <i>g</i><sub>0</sub> + <i>g</i><sub>–1</sub>, annehmen kann.<br> | ||
| Zeile 50: | Zeile 50: | ||
Ein Schwellenwertentscheider (mit der Schwelle bei <i>E</i> = 0.5) würde bei diesen dargestellten zehn Bit mindestens eine Fehlentscheidung treffen (bei <i>ν</i> = 4), und eventuell eine weitere bei <i>ν</i> = 2, falls <i>d</i><sub>2</sub> geringfügig kleiner ist als der Schwellenwert <i>E</i> = 0.5. Dagegen wird der Viterbi–Empfänger diese Folge der Länge 10 richtig entscheiden, wie auf den nächsten Seiten gezeigt werden wird.{{end}}<br> | Ein Schwellenwertentscheider (mit der Schwelle bei <i>E</i> = 0.5) würde bei diesen dargestellten zehn Bit mindestens eine Fehlentscheidung treffen (bei <i>ν</i> = 4), und eventuell eine weitere bei <i>ν</i> = 2, falls <i>d</i><sub>2</sub> geringfügig kleiner ist als der Schwellenwert <i>E</i> = 0.5. Dagegen wird der Viterbi–Empfänger diese Folge der Länge 10 richtig entscheiden, wie auf den nächsten Seiten gezeigt werden wird.{{end}}<br> | ||
| − | + | == | |
{{Display}} | {{Display}} | ||
Version vom 27. Dezember 2016, 16:12 Uhr
Blockschaltbild und Voraussetzungen für Kapitel 3.8 (1)
Der Korrelationsempfänger ist im Sinne der Maximum–Likelihood–Entscheidungsregel optimal, das heißt, er führt bei gleichwahrscheinlichen Quellensymbolen zur minimalen Fehlerwahrscheinlichkeit. Nachteilig ist:
- Der Realisierungsaufwand steigt exponentiell mit der Länge N der zu detektierenden Symbolfolge.
- Da die Folge gemeinsam entschieden wird, kommt es bei großem N zu langen Verzögerungen.
In den 1970er Jahren hat Andrew J. Viterbi einen ML–Empfänger vorgeschlagen, der die Detektion von Teilen der empfangenen Nachricht erlaubt und bei dem sich der Realisierungsaufwand auch bei unendlich langen Folgen in Grenzen hält.
Zu den einzelnen Komponenten des Blockschaltbildes ist anzumerken:
- Das an den Empfangsgrundimpuls und die Störung angepasste Matched–Filter HMF(f) dient der Störleistungsbegrenzung. Das MF–Ausgangssignal m(t) bzw. die Folge 〈mν〉 der äquidistanten Signalwerte nach der Abtastung besitzt das bestmögliche Signal–zu–Stör–Leistungsverhältnis.
- Aufgabe des Dekorrelationsfilters HDF(f) ist es, aus der Folge 〈mν〉 die Detektionsabtastwerte dν = dSν + dNν zu gewinnen, deren Störanteile dNν unkorreliert sind. Dieses Filter wird deshalb auch Whitening–Filter genannt.
- Der Viterbi–Entscheider, der im Mittelpunkt der folgenden Betrachtungen steht, gewinnt aus der Folge 〈dν〉 seiner wertkontinuierlichen Eingangswerte die binäre Ausgangsfolge 〈υν〉 entsprechend der Maximum–Likelihood–Regel mit der kleinstmöglichen Fehlerwahrscheinlichkeit Pr(υν ≠ qν).
Die Beschreibung wird auf der nächsten Seite fortgesetzt.
Blockschaltbild und Voraussetzungen für Kapitel 3.8 (2)
Um den Viterbi–Algorithmus möglichst einfach beschreiben und veranschaulichen zu können, werden hier einige vereinfachende Voraussetzungen getroffen:
- Die Amplitudenkoeffizienten seien unipolar ⇒ aν ∈ {0, 1}. Anzumerken ist, dass es bei der Verwendung bipolarer Koeffizienten aν ∈ {–1, +1} nur weniger Modifikationen bedarf.
- Der Grundimpuls gd(t) besteht nur aus dem Hauptwert g0 = gd(t = TD) und einem Vorläufer g–1 = gd(t = TD – T).
- Damit ergeben sich für die wertkontinuierlichen Detektionsabtastwerte
- \[d_{\nu} = a_{\nu}\cdot g_{0} + a_{\nu+1}\cdot g_{-1}+d_{{\rm N}\nu} \hspace{0.05cm},\]
- wobei die Rauschkomponente dNν als gaußverteilt angenommen wird (Streuung σd).
Bei bipolarer Signalisierung ist der Algorithmus nicht aufwändiger. Dagegen steigt der Rechenaufwand, wenn der Detektionsgrundimpuls breiter wird und mehr als nur einen Vorläufer g–1 aufweist. Die Vernachlässigung von Nachläufern stellt keine grundlegende Einschränkung dar, weil jeder Impuls gd(t) diese Bedingung durch geeignete Wahl des Detektionszeitpunktes TD erfüllen kann. Anzumerken ist weiter, dass im Folgenden alle Signalwerte auf 1 normiert werden.
g0 + g–1, annehmen kann.
Die am Viterbi–Entscheider anstehenden Abtastwerte (rote Punkte) sind d0 = 0.2, d1 = 0.7, d2 = 0.5, d3 = 0, ... , wobei die Differenzen dNν = dν – dSν von einer AWGN–Rauschquelle herrühren.
==