Digitalsignalübertragung/Struktur des optimalen Empfängers: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 106: | Zeile 106: | ||
| − | == == | + | == Das Theorem der Irrelevanz (1) == |
| + | <br> | ||
| + | Zu beachten ist, dass der auf der letzten Seite beschriebene Empfänger nur dann optimal ist, wenn auch der Detektor bestmöglich implementiert ist, das heißt, wenn durch den Übergang vom kontinuierlichen Signal <i>r</i>(<i>t</i>) zum Vektor <i><b>r</b></i> keine Information verloren geht.<br> | ||
| + | |||
| + | Um die Frage zu klären, welche und wieviele Messungen am Empfangssignal <i>r</i>(<i>t</i>) durchzuführen sind, um Optimalität zu garantieren, ist das <i>Theorem der Irrelevanz</i> hilfreich. Dazu betrachten wir den nachfolgend skizzierten Empfänger, dessen Detektor aus dem Empfangssignal <i>r</i>(<i>t</i>) die zwei Vektoren <i><b>r</b></i><sub>1</sub> und <i><b>r</b></i><sub>2</sub> ableitet und dem Entscheider zur Verfügung stellt. <i><b>r</b></i><sub>1</sub> und <i><b>r</b></i><sub>2</sub> stehen mit der Nachricht <i>m</i> ∈ {<i>m<sub>i</sub></i>} über die Verbundwahrscheinlichkeitsdichte <i>p</i><sub><i><b>r</b></i><sub>1</sub>, <i><b>r</b></i><sub>2</sub>|<i>m</i></sub> in Zusammenhang.<br> | ||
| + | |||
| + | [[Datei:P ID2003 Dig T 4 2 S3a version2.png|Zum Theorem der Irrelevanz|class=fit]]<br> | ||
| + | |||
| + | Die Entscheidungsregel des MAP–Empfängers lautet mit Anpassung an dieses Beispiel: | ||
| + | |||
| + | :<math>\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2|m_i )]=</math> | ||
| + | :::<math>\hspace{-0.1cm} = \hspace{-0.1cm} | ||
| + | {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | |m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )] | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Hierzu ist anzumerken: | ||
| + | *Die Vektoren <i><b>r</b></i><sub>1</sub> und <i><b>r</b></i><sub>2</sub> sind Zufallsgrößen. Ihre Realisierungen werden hier und im Folgenden mit <i><b>ρ</b></i><sub>1</sub> und <i><b>ρ</b></i><sub>2</sub> bezeichnet. Zur Hervorhebung sind alle Vektoren in der Grafik rot eingetragen. | ||
| + | *Die Voraussetzungen für die Anwendung des „Theorems der Irrelevanz” sind die gleichen wie die an eine Markovkette erster Ordnung. Die Zufallsvariablen <i>x</i>, <i>y</i>, <i>z</i> formen dann eine solche, falls die Verteilung von <i>z</i> bei gegebenem <i>y</i> unabhängig von <i>x</i> ist: | ||
| + | |||
| + | ::<math>p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|y) \hspace{0.25cm} {\rm anstelle \hspace{0.15cm}von} \hspace{0.25cm}p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|x, y) \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Der optimale Empfänger muss im allgemeinen Fall beide Vektoren <i><b>r</b></i><sub>1</sub> und <i><b>r</b></i><sub>2</sub> auswerten, da in obiger Entscheidungsregel beide Verbundwahrscheinlichkeitsdichten <i>p</i><sub><i><b>r</b></i><sub>1</sub>|<i>m</i></sub> und <i>p</i><sub><i><b>r</b></i><sub>2</sub>| <i><b>r</b></i><sub>1</sub>, <i>m</i></sub> auftreten. | ||
| + | |||
| + | *Dagegen kann der Empfänger ohne Informationseinbuße die zweite Messung vernachlässigen, falls <i><b>r</b></i><sub>2</sub> bei gegebenem <i><b>r</b></i><sub>1</sub> unabhängig von der Nachricht <i>m</i> ist: | ||
| + | |||
| + | ::<math>p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= | ||
| + | p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 ) | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *In diesem Fall lässt sich die Entscheidungsregel weiter vereinfachen: | ||
| + | |||
| + | ::<math>\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} | ||
| + | {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | |m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )]= </math> | ||
| + | ::::<math> = \hspace{-0.1cm} | ||
| + | {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | |m_i ) | ||
| + | \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 )]=</math> | ||
| + | ::::<math> = \hspace{-0.1cm} | ||
| + | {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 | ||
| + | |m_i ) | ||
| + | ] | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | |||
{{Display}} | {{Display}} | ||
Version vom 28. Dezember 2016, 12:07 Uhr
Inhaltsverzeichnis
Blockschaltbild und Voraussetzungen
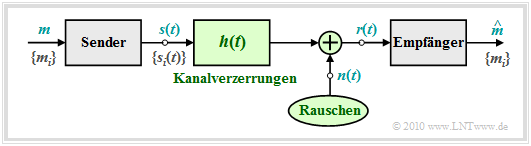
In diesem Kapitel wird die Struktur des optimalen Empfängers eines digitalen Übertragungssystems sehr allgemein hergeleitet, wobei
- das Modulationsverfahren und weitere Systemdetails nicht weiter spezifiziert werden,
- von den Basisfunktionen und der Signalraumdarstellung gemäß Kapitel 4.1 ausgegangen wird..
Zum obigen Blockschaltbild ist anzumerken:
- Der Symbolumfang der Quelle beträgt M und der Symbolvorrat ist {mi} mit i = 0, ... , M – 1. Die zugehörigen Symbolwahrscheinlichkeiten Pr(m = mi) seien auch dem Empfänger bekannt.
- Zur Nachrichtenübertragung stehen M verschiedene Signalformen si(t) zur Verfügung, wobei für die Laufvariable ebenfalls die Indizierung i = 0, ... , M – 1 gelten soll.
- Es besteht eine feste Beziehung zwischen den Nachrichten {mi} und den Signalen {si(t)}. Wird die Nachricht m = mi übertragen, so ist das Sendesignal s(t) = si(t).
- Lineare Kanalverzerrungen sind in der obigen Grafik durch die Impulsantwort h(t) berücksichtigt. Außerdem ist ein (irgendwie geartetes) Rauschen n(t) wirksam.
- Mit diesen beiden die Übertragung störenden Effekten lässt sich das am Empfänger ankommende Signal r(t) in folgender Weise angeben:
- \[r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.\]
- Aufgabe des (optimalen) Empfängers ist es, anhand seines Eingangssignals r(t) herauszufinden, welche der M möglichen Nachrichten mi – bzw. welches der Signale si(t) – gesendet wurde.
- Der vom Empfänger gefundene Schätzwert für m wird in Gleichungen durch ein „Circonflexe” (^) gekennzeichnet. Im Fließtext (HTML–Zeichensatz) ist diese Darstellung leider nicht möglich.
- Man spricht von einem optimalen Empfänger, wenn die Symbolfehlerwahrscheinlichkeit den für die Randbedingungen kleinstmöglichsten Wert annimmt:
- \[p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm Minimum} \hspace{0.05cm}.\]
Hinweis: Im Folgenden wird meist r(t) = s(t) + n(t) vorausgesetzt, was bedeutet, dass h(t) = δ(t) als verzerrungsfrei angenommen wird. Andernfalls könnten wir die Signale si(t) als s'i(t) = si(t) ∗ h(t) neu definieren, also die deterministischen Kanalverzerrungen dem Sendesignal beaufschlagen.
Fundamentaler Ansatz zum optimalen Empfängerentwurf (1)
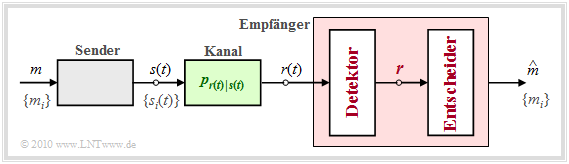
Gegenüber dem auf der vorherigen Seite gezeigten Blockschaltbild führen wir nun einige wesentliche Verallgemeinerungen durch:
- Der Übertragungskanal wird durch die bedingte Wahrscheinlichkeitsdichtefunktion pr(t)|s(t) beschrieben, welche die Anhängigkeit des Empfangssignals r(t) vom Sendesignal s(t) festlegt.
- Wurde nun ein ganz bestimmtes Signal r(t) = ρ(t) empfangen, so hat der Empfänger die Aufgabe, anhand dieses Signals ρ(t) sowie der M bedingten Wahrscheinlichkeitsdichtefunktionen
- \[p_{r(t) | s(t) } (\rho(t) | s_i(t))\hspace{0.2cm}{\rm mit}\hspace{0.2cm} i = 0, ... \hspace{0.05cm}, M-1\]
- unter Berücksichtigung aller möglichen Sendesignale si(t) und deren Auftrittswahrscheinlichkeiten Pr(m = mi) herauszufinden, welche der möglichen Nachrichten (mi) bzw. welches der möglichen Signale (si(t)) am wahrscheinlichsten gesendet wurde.
- Die Schätzung des optimalen Empfängers ist also ganz allgemein bestimmt durch die Gleichung
- \[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{s(t) | r(t) } ( s_i(t) | \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m | r(t) } ( m_i | \rho(t))\hspace{0.05cm},\]
- wobei wieder berücksichtigt ist, dass die gesendete Nachricht m = mi und das gesendete Signal s(t) = si(t) eineindeutig ineinander übergeführt werden können.
In anderen Worten: Der optimale Empfänger betrachtet diejenige Nachricht mi als die gesendete, wenn die bedingte Wahrscheinlichkeitsdichtefunktion pm|r(t) für das anliegende Empfangssignal ρ(t) sowie unter der Annahme m = mi den größtmöglichen Wert annimmt.
Bevor wir die obige Entscheidungsregel näher diskutieren, soll der optimale Empfänger entsprechend der Grafik noch in zwei Funktionsblöcke aufgeteilt werden:
- Der Detektor nimmt am Empfangssignal r(t) verschiedene Messungen vor und fasst diese im Vektor r zusammen. Bei K Messungen entspricht r einem Punkt im K–dimensionalen Vektorraum.
- Der Entscheider bildet abhängig von diesem Vektor den Schätzwert. Bei einem gegebenen Vektor r = ρ lautet dabei die Entscheidungsregel:
- \[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) \hspace{0.05cm}.\]
Im Gegensatz zur oberen Gleichung tritt nun in der Entscheidungsregel eine bedingte Wahrscheinlichkeit Pm|r anstelle der bedingten Wahrscheinlichkeitskeitsdichtefunktion (WDF) pm|r(t) auf. Beachten Sie bitte die Groß– bzw. Kleinschreibung für die unterschiedlichen Bedeutungen.
Fundamentaler Ansatz zum optimalen Empfängerentwurf (2)
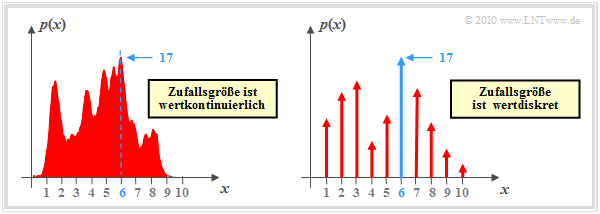
Wir betrachten nun die Funktion y = arg max p(x), wobei p(x) die Wahrscheinlichkeitsdichtefunktion (WDF) einer wertkontinuierlichen oder wertdiskreten Zufallsgröße x beschreibt. Im zweiten Fall besteht die WDF aus einer Summe von Diracfunktionen mit den Wahrscheinlichkeiten als Impulsgewichte.
Die Grafik zeigt beispielhafte Funktionen. In beiden Fällen liegt das WDF–Maximum (17) bei x = 6:
\[\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},\hspace{0.2cm}y = {\rm arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.\]
Man nennt die (bedingten) Wahrscheinlichkeiten in der Gleichung
\[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho})\]
auch a–Posteriori–Wahrscheinlichkeiten. Mit dem Satz von Bayes kann hierfür geschrieben werden:
\[P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) = \frac{{\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )}{p_{\boldsymbol{ r}} (\boldsymbol{\rho})} \hspace{0.05cm}.\]
Da der Term im Nenner für alle mi gleich ist, muss er für die Entscheidung nicht weiter berücksichtigt werden. Damit erhält man die folgenden Regeln:
\[\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )]\hspace{0.05cm}.\]
Der Vorteil dieser Gleichung ist, dass die die Vorwärtsrichtung des Kanals beschreibende bedingte WDF pr|m („Ausgang unter der Bedingung Eingang”) verwendet werden kann. Dagegen verwendet die erste Gleichung die Rückschlusswahrscheinlichkeiten Pm|r („Eingang unter der Bedingung Ausgang”).
\[\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )\hspace{0.05cm}.\]
Bei diesem werden die möglicherweise unterschiedlichen Auftrittswahrscheinlichkeiten Pr(mi) für den Entscheidungsprozess nicht herangezogen, zum Beispiel, weil sie dem Empfänger nicht bekannt sind.
Hinweis: Im Kapitel 3.7 finden Sie eine andere Herleitung. Allgemein gilt: Bei gleichwahrscheinlichen Nachrichten {mi} ⇒ Pr(mi) = 1/M ist der ML–Empfänger gleichwertig mit dem MAP–Empfänger:
\[\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )\hspace{0.05cm}.\]
Das Theorem der Irrelevanz (1)
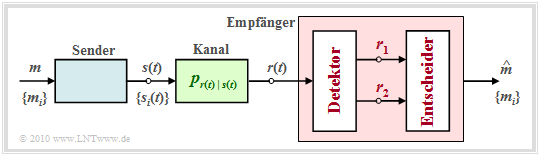
Zu beachten ist, dass der auf der letzten Seite beschriebene Empfänger nur dann optimal ist, wenn auch der Detektor bestmöglich implementiert ist, das heißt, wenn durch den Übergang vom kontinuierlichen Signal r(t) zum Vektor r keine Information verloren geht.
Um die Frage zu klären, welche und wieviele Messungen am Empfangssignal r(t) durchzuführen sind, um Optimalität zu garantieren, ist das Theorem der Irrelevanz hilfreich. Dazu betrachten wir den nachfolgend skizzierten Empfänger, dessen Detektor aus dem Empfangssignal r(t) die zwei Vektoren r1 und r2 ableitet und dem Entscheider zur Verfügung stellt. r1 und r2 stehen mit der Nachricht m ∈ {mi} über die Verbundwahrscheinlichkeitsdichte pr1, r2|m in Zusammenhang.
Die Entscheidungsregel des MAP–Empfängers lautet mit Anpassung an dieses Beispiel:
\[\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2|m_i )]=\]
- \[\hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )] \hspace{0.05cm}.\]
Hierzu ist anzumerken:
- Die Vektoren r1 und r2 sind Zufallsgrößen. Ihre Realisierungen werden hier und im Folgenden mit ρ1 und ρ2 bezeichnet. Zur Hervorhebung sind alle Vektoren in der Grafik rot eingetragen.
- Die Voraussetzungen für die Anwendung des „Theorems der Irrelevanz” sind die gleichen wie die an eine Markovkette erster Ordnung. Die Zufallsvariablen x, y, z formen dann eine solche, falls die Verteilung von z bei gegebenem y unabhängig von x ist:
- \[p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|y) \hspace{0.25cm} {\rm anstelle \hspace{0.15cm}von} \hspace{0.25cm}p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|x, y) \hspace{0.05cm}.\]
- Der optimale Empfänger muss im allgemeinen Fall beide Vektoren r1 und r2 auswerten, da in obiger Entscheidungsregel beide Verbundwahrscheinlichkeitsdichten pr1|m und pr2| r1, m auftreten.
- Dagegen kann der Empfänger ohne Informationseinbuße die zweite Messung vernachlässigen, falls r2 bei gegebenem r1 unabhängig von der Nachricht m ist:
- \[p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 ) \hspace{0.05cm}.\]
- In diesem Fall lässt sich die Entscheidungsregel weiter vereinfachen:
- \[\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm}
{\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1
|m_i )
\cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )]= \]
- \[ = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 )]=\]
- \[ = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) ] \hspace{0.05cm}.\]