Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit: Unterschied zwischen den Versionen

Version vom 28. Dezember 2016, 14:39 Uhr

Optimale Entscheidung bei binärer Übertragung (1)

Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: r = s + n:

Der das Übertragungssystem vollständig beschreibende Vektorraum wird von N = 2 zueinander orthogonalen Basisfunktionen φ₁(t) und φ₂(t) aufgespannt.

Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor n = (n₁, n₂).

Es gibt nur zwei mögliche Sendesignale (M = 2), die durch die beiden Vektoren s₀ = (s₀₁, s₀₂) und s₁ = (s₁₁, s₁₂) beschrieben werden:

\[s_0(t) \hspace{-0.1cm} = \hspace{-0.1cm} s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},\]

\[s_1(t) \hspace{-0.1cm} = \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.\]

Die beiden Nachrichten m₀ ⇔ s₀ und m₁ ⇔ s₁ sind nicht notwendigermaßen gleichwahrscheinlich.

Aufgabe des Entscheiders ist es nun, für den gegebenen Empfangsvektor r einen Schätzwert nach der MAP–Entscheidungsregel anzugeben. Diese lautet im vorliegenden Fall:

\[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_i ) ] \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} \boldsymbol{ r } = \boldsymbol{ \rho } = (\rho_1, \rho_2) \hspace{0.05cm}.\]

Im hier betrachteten Sonderfall N = 2 und M = 2 partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete I₀ und I₁, wie in der nachfolgenden Grafik verdeutlicht. Liegt der Empfangswert in I₀, so wird als Schätzwert m₀ ausgegeben, andernfalls m₁.

Die Herleitung und Bildbeschreibung folgt auf der nächsten Seite.

@@ Zeile 6: / Zeile 6: @@
 }}
+== Optimale Entscheidung bei binärer Übertragung (1) ==
+<br>
+Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: <b><i>r</i></b> = <b><i>s</i></b> + <b><i>n</i></b>:
+*Der das Übertragungssystem vollständig beschreibende Vektorraum wird von <i>N</i> = 2 zueinander orthogonalen Basisfunktionen <i>&phi;</i><sub>1</sub>(<i>t</i>) und <i>&phi;</i><sub>2</sub>(<i>t</i>) aufgespannt.<br>
+*Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor <b><i>n</i></b> = (<i>n</i><sub>1</sub>,  <i>n</i><sub>2</sub>).<br>
+*Es gibt nur zwei mögliche Sendesignale (<i>M</i> = 2), die durch die beiden Vektoren <b><i>s</i></b><sub>0</sub> = (<i>s</i><sub>01</sub>, <i>s</i><sub>02</sub>) und <b><i>s</i></b><sub>1</sub> = (<i>s</i><sub>11</sub>, <i>s</i><sub>12</sub>) beschrieben werden:
+::<math>s_0(t) \hspace{-0.1cm}  =  \hspace{-0.1cm} s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},</math>
+::<math>s_1(t) \hspace{-0.1cm}  =  \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.</math>
+*Die beiden Nachrichten <i>m</i><sub>0</sub> &#8660; <b><i>s</i></b><sub>0</sub> und <i>m</i><sub>1</sub> &#8660; <i>'''s'''</i><sub>1</sub> sind nicht notwendigermaßen gleichwahrscheinlich.<br>
+*Aufgabe des Entscheiders ist es nun, für den gegebenen Empfangsvektor <b><i>r</i></b> einen Schätzwert nach der [http://www.lntwww.de/Digitalsignal%C3%BCbertragung/Struktur_des_optimalen_Empf%C3%A4ngers#Fundamentaler_Ansatz_zum_optimalen_Empf.C3.A4ngerentwurf_.281.29 MAP&ndash;Entscheidungsregel] anzugeben. Diese lautet im vorliegenden Fall:
+::<math>\hat{m} = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_i ) ]
+\hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\}\hspace{0.3cm}{\rm mit}\hspace{0.3cm}
+\boldsymbol{ r } = \boldsymbol{ \rho } = (\rho_1, \rho_2)
+\hspace{0.05cm}.</math>
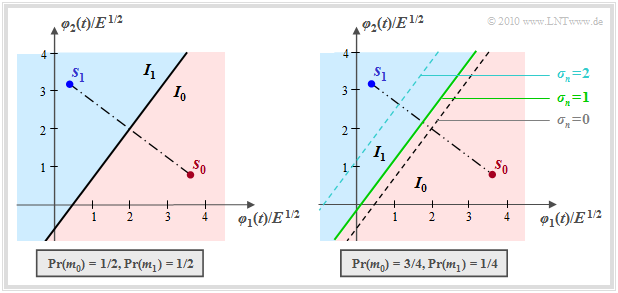
+Im hier betrachteten Sonderfall <i>N</i> = 2 und <i>M</i> = 2 partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete <i>I</i><sub>0</sub> und <i>I</i><sub>1</sub>, wie in der nachfolgenden Grafik verdeutlicht. Liegt der Empfangswert in <i>I</i><sub>0</sub>, so wird als Schätzwert <i>m</i><sub>0</sub> ausgegeben, andernfalls <i>m</i><sub>1</sub>.
+[[Datei:P ID2019 Dig T 4 3 S1 version1.png|Entscheidungsregionen für gleiche (links) bzw. ungleiche (rechts) Auftrittswahrscheinlichkeiten|class=fit]]<br>
+Die Herleitung und Bildbeschreibung folgt auf der nächsten Seite.<br>
 {{Display}}