Aufgaben:Aufgabe 2.4Z: Tiefpass-Einfluss bei Synchrondemodulation: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 22: | Zeile 22: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welche Aussagen sind über das Filter $H_E(f)$ möglich, das zur Gewinnung des auf der Angabenseite dargestellten Sinkensignals benutzt wurde? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + Die obere Grenzfrequenz ist zu hoch. |
| − | + | - Die obere Grenzfrequenz ist zu niedrig. | |
| + | - Die untere Grenzfrequenz ist ungleich 0. | ||
| + | {Mit welchen der nachfolgend aufgeführten Tiefpassfunktionen ist eine ideale Demodulation – das heißt $υ(t) = q(t)$ – prinzipiell möglich? | ||
| + | |type="[]"} | ||
| + | + Rechtecktiefpass. | ||
| + | - Gaußtiefpass. | ||
| + | + Trapeztiefpass. | ||
| + | - Spalttiefpass. | ||
| + | |||
| + | {Wie ist die untere Eckfrequenz $f_1$ eines Trapeztiefpasses mindestens zu wählen, damit keine Verzerrungen entstehen? | ||
| + | |type="{}"} | ||
| + | $f_{1, min}$= { 5 3 % } $\text{KHz}$ | ||
| − | { | + | {Wie groß darf die obere Eckfrequenz $f_2$ des Trapeztiefpasses höchstens sein, damit keine Verzerrungen entstehen? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{2,max}$ = { 95 3% } $\text{KHz}$ |
| + | |||
| + | |||
| + | {Welche Grenzfrequenz $f_G$ eines idealen, rechteckförmigen Tiefpasses würden Sie bevorzugen, wenn Rauschstörungen nicht zu vernachlässigen sind? | ||
| + | |type="[]"} | ||
| + | - $f_G = 4 kHz,$ | ||
| + | + $f_G = 6 kHz,$ | ||
| + | - $f_G = 10 kHz.$ | ||
Version vom 30. Dezember 2016, 18:25 Uhr
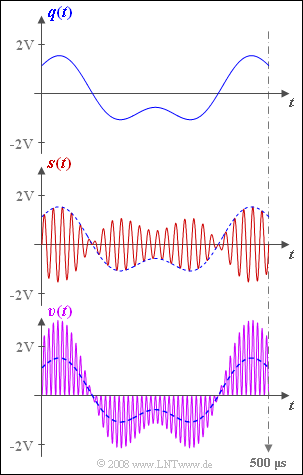
Wir betrachten das gleiche Übertragungssystem wie in Aufgabe A2.4. Es wird nun allerdings stets eine perfekte Frequenz– und Phasensynchronisation des Synchrondemodulators (SD) vorausgesetzt. Das Quellensignal $q(t)$, das Sendesignal $s(t)$ sowie das Signal $b(t)$ vor dem Tiefpassfilter innerhalb des Synchrondemodulators sind wie folgt gegeben: $$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm mit }$$ $$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ $$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ $$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ $$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ Die Grafik zeigt zunächst die Signale $q(t)$ und $s(t)$. In der letzten Skizze ist das Sinkensignal $υ(t)$ dargestellt (violetter Kurvenverlauf). Dieses stimmt offensichtlich nicht mit dem Quellensignal (blau-gestrichelte Kurve) überein. Der Grund für das unerwünschte Ergebnis $υ(t) ≠ q(t)$ könnte zum Beispiel ein fehlender oder falsch dimensionierter Tiefpass sein.
In den Teilaufgaben c) und d) wird der sogenannte $\text{Trapeztiefpass}$ verwendet, dessen Frequenzgang wie folgt lautet: $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$ Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.2. Im Gegensatz zur Aufgabe A2.4 beschreiben hier f1 und f2 nicht die Signalfrequenzen, sondern beziehen sich auf das Tiefpassfilter.
Fragebogen
Musterlösung