Aufgaben:Aufgabe 3.6: PM oder FM? Oder AM?: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Frequenzmodulation (FM) }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |t…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1102__Mod_A_3_6.png|right|]] |
| + | Zur Analyse eines Modulators wird an seinen Eingang das Signal | ||
| + | $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ | ||
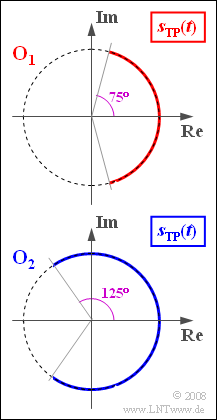
| + | angelegt, wobei die Signalamplitude stets $A_N = 2 V$ beträgt. Mit der Signalfrequenz $f_N = f_1 = 5 kHz$ wird die Ortskurve $O_1$ ermittelt. Verwendet man die Nachrichtenfrequenz $f_N = f_2$, so stellt sich die Ortskurve $O_2$ ein. | ||
| + | |||
| + | Beachten Sie bei Ihrer Lösung, dass bei Winkelmodulation – dies ist der Sammelbegriff für Phasen– und Frequenzmodulation – der folgende Zusammenhang zwischen dem Modulationsindex $η$ und der Modulatorkonstanten $K_{WM}$ besteht: | ||
| + | $$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$ | ||
| + | '''Hinweis:''' Die Aufgabe bezieht sich wieder auf die Theorieteile von [http://www.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1] und [http://www.lntwww.de/Modulationsverfahren/Frequenzmodulation_(FM) Kapitel 3.2]. | ||
| + | |||
Version vom 3. Januar 2017, 16:20 Uhr
Zur Analyse eines Modulators wird an seinen Eingang das Signal $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ angelegt, wobei die Signalamplitude stets $A_N = 2 V$ beträgt. Mit der Signalfrequenz $f_N = f_1 = 5 kHz$ wird die Ortskurve $O_1$ ermittelt. Verwendet man die Nachrichtenfrequenz $f_N = f_2$, so stellt sich die Ortskurve $O_2$ ein.
Beachten Sie bei Ihrer Lösung, dass bei Winkelmodulation – dies ist der Sammelbegriff für Phasen– und Frequenzmodulation – der folgende Zusammenhang zwischen dem Modulationsindex $η$ und der Modulatorkonstanten $K_{WM}$ besteht: $$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$ Hinweis: Die Aufgabe bezieht sich wieder auf die Theorieteile von Kapitel 3.1 und Kapitel 3.2.
Fragebogen
Musterlösung