Aufgaben:Aufgabe 3.10Z: Amplituden- und Winkelmodulation im Vergleich: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Rauscheinfluss bei Winkelmodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Cho…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1112__Mod_Z_3_9.png|right|]] |
| + | Betrachtet wird die Übertragung eines Cosinussignals mit Amplitudenmodulation und Winkelmodulation. Es gelten folgende Randbedingungen: | ||
| + | :* Nachrichtenfrequenz $f_N = 10 kHz$, | ||
| + | :* Sendeleistung $P_S = 100 kW$, | ||
| + | :* Kanaldämpfungsfaktor $20 · lg α_K = –120 dB$, | ||
| + | :* Rauschleistungsdichte $N_0 = 10^{–16} W/Hz$. | ||
| + | Diese Systemparameter werden zweckmäßigerweise zur gemeinsamen Leistungskenngröße | ||
| + | $$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ | ||
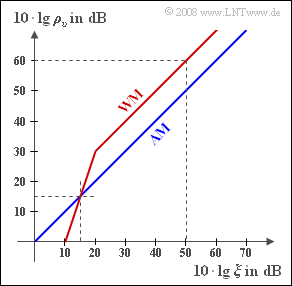
| + | zusammengefasst. Die Grafik zeigt den sich ergebenden Sinken–Störabstand $10 · lg ρ_υ$ in Abhängigkeit der logarithmierten Leistungskenngröße $ξ$. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://www.lntwww.de/Modulationsverfahren/Synchrondemodulation Kapitel 2.2] , [http://www.lntwww.de/Modulationsverfahren/Frequenzmodulation_(FM) Kapitel 3.2] und [http://www.lntwww.de/Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation Kapitel 3.3]. Es gelten folgende Beziehungen: | ||
| + | $$\rho_{v } = \left\{ \begin{array}{c} \xi \\ {\eta^2}/2 \cdot\xi \\ 3{\eta^2}/2 \cdot\xi \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}l} {\rm ZSB/ESB-AM \hspace{0.15cm}ohne \hspace{0.15cm}Tr\ddot{a}ger} \hspace{0.05cm}, \\ {\rm PM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta } \hspace{0.05cm}, \\ {\rm FM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta }\hspace{0.05cm}. \\ \end{array}$$ | ||
| + | Die Bandbreiten bei Winkelmodulation sind so zu wählen, dass ein Klirrfaktor K kleiner als 1% garantiert werden kann ('''Carson–Regel'''): | ||
| + | $$ B_{\rm K} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.05cm}.$$ | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 3. Januar 2017, 18:39 Uhr
Betrachtet wird die Übertragung eines Cosinussignals mit Amplitudenmodulation und Winkelmodulation. Es gelten folgende Randbedingungen:
- Nachrichtenfrequenz $f_N = 10 kHz$,
- Sendeleistung $P_S = 100 kW$,
- Kanaldämpfungsfaktor $20 · lg α_K = –120 dB$,
- Rauschleistungsdichte $N_0 = 10^{–16} W/Hz$.
Diese Systemparameter werden zweckmäßigerweise zur gemeinsamen Leistungskenngröße $$ \xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ zusammengefasst. Die Grafik zeigt den sich ergebenden Sinken–Störabstand $10 · lg ρ_υ$ in Abhängigkeit der logarithmierten Leistungskenngröße $ξ$.
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.2 , Kapitel 3.2 und Kapitel 3.3. Es gelten folgende Beziehungen: $$\rho_{v } = \left\{ \begin{array}{c} \xi \\ {\eta^2}/2 \cdot\xi \\ 3{\eta^2}/2 \cdot\xi \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}l} {\rm ZSB/ESB-AM \hspace{0.15cm}ohne \hspace{0.15cm}Tr\ddot{a}ger} \hspace{0.05cm}, \\ {\rm PM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta } \hspace{0.05cm}, \\ {\rm FM \hspace{0.15cm}mit \hspace{0.15cm}Modulationsgrad \hspace{0.15cm} \eta }\hspace{0.05cm}. \\ \end{array}$$ Die Bandbreiten bei Winkelmodulation sind so zu wählen, dass ein Klirrfaktor K kleiner als 1% garantiert werden kann (Carson–Regel): $$ B_{\rm K} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.05cm}.$$
Fragebogen
Musterlösung