Aufgaben:Aufgabe 3.3: Vom Signal zum Spektrum: Unterschied zwischen den Versionen
Aus LNTwww
| (16 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID503__Sig_A_3_3.png|250px|right|Rechteckimpuls und Spektrum]] | + | [[Datei:P_ID503__Sig_A_3_3.png|250px|right|frame|Rechteckimpuls und zugehöriges Spektrum]] |
| − | Betrachtet wird ein Rechteckimpuls $x(t)$ der Dauer $T = 50\,\text{µs}$ und der Höhe $A = 2\,\text{V}$. An den Sprungstellen bei $t = 0$ und $t = T$ ist der Signalwert jeweils $A/2$, was aber für die Lösung der Aufgabe keinen Einfluss hat. | + | Betrachtet wird ein Rechteckimpuls $x(t)$ der Dauer $T = 50\,\text{µs}$ und der Höhe $A = 2\,\text{V}$. An den Sprungstellen bei $t = 0$ und $t = T$ ist der Signalwert jeweils $A/2$, was aber für die Lösung der Aufgabe keinen Einfluss hat. |
| − | In der unteren Grafik ist die dazugehörige Spektralfunktion nach Betrag und Phase qualitativ skizziert. Es gilt: | + | In der unteren Grafik ist die dazugehörige Spektralfunktion nach Betrag und Phase qualitativ skizziert. Es gilt: |
| − | $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$ | + | :$$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$ |
| − | Der analytische Funktionsverlauf von $X(f)$ soll ermittelt werden. | + | Der analytische Funktionsverlauf von $X(f)$ soll ermittelt werden. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale|Einige Sonderfälle impulsartiger Signale]]. |
| − | + | ||
*Gegeben sind weiterhin folgende trigonometrischen Umformungen: | *Gegeben sind weiterhin folgende trigonometrischen Umformungen: | ||
| − | $$\sin ^2( \alpha ) = {1}/{2} \cdot \ | + | :$$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$ |
| Zeile 25: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie allgemein die Spektralfunktion $X(f)$. Welcher Wert ergibt sich bei der Frequenz $f=10\, \text{kHz} | + | {Berechnen Sie allgemein die Spektralfunktion $X(f)$. Welcher Wert ergibt sich bei der Frequenz $f=10\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}[X(f=10 \,\text{kHz})]$ | + | ${\rm Re}\big[X(f=10 \,\text{kHz})\big] \ = \ $ { 0. } $\text{mV/Hz}$ |
| − | ${\rm | + | ${\rm Im}\big[X(f=10\, \text{kHz})\big]\ = \ $ { -0.064--0.06 } $\text{mV/Hz}$ |
| − | {Berechnen Sie die Betragsfunktion $|X(f)|$ allgemein. Welche Werte ergeben sich für die Frequenzen $f = 0$ und $f=20 \,\text{kHz} | + | {Berechnen Sie die Betragsfunktion $|X(f)|$ allgemein. Welche Werte ergeben sich für die Frequenzen $f = 0$ und $f=20 \,\text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $|X(f=0)|$ | + | $|X(f=0)|\ = \ $ { 0.1 3% } $\text{mV/Hz}$ |
| − | $|X(f=20\, \text{kHz})| | + | $|X(f=20\, \text{kHz})|\ = \ $ { 0. } $\text{mV/Hz}$ |
| − | {Welche der folgenden Aussagen sind bezüglich $|X(f)|$ zutreffend? | + | {Welche der folgenden Aussagen sind bezüglich $|X(f)|$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + $|X(f)|$ hat Nullstellen bei Vielfachen von $f_0 = 1/T$. | + | + $|X(f)|$ hat Nullstellen bei Vielfachen von $f_0 = 1/T$. |
| − | - $|X(f)|$ hat Nullstellen bei Vielfachen von $f_0 = 1/(2T)$. | + | - $|X(f)|$ hat Nullstellen bei Vielfachen von $f_0 = 1/(2T)$. |
| − | + In der Mitte zwischen zwei Nullstellen gilt $|X(f)| = |A/(\pi f)|$. | + | + In der Mitte zwischen zwei Nullstellen gilt $|X(f)| = |A/(\pi f)|$. |
| − | {Berechnen Sie die Phasenfunktion $\varphi (f)$. Welcher Phasenwinkel (in Grad) ergibt sich bei der Frequenz $f=10\, \text{kHz}$? | + | {Berechnen Sie die Phasenfunktion $\varphi (f)$. Welcher Phasenwinkel (in Grad) ergibt sich bei der Frequenz $f=10\, \text{kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi (f=10\, \text{kHz}) | + | $\varphi (f=10\, \text{kHz})\ = \ $ { 90 1% } $\text{Grad}$ |
| Zeile 50: | Zeile 56: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Mit der Abkürzung $\omega = 2\pi f$ lautet die Spektralfunktion gemäß dem ersten Fourierintegral: |
| − | $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$ | + | :$$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$ |
| − | Nach Integration und Einsetzen der Grenzen folgt daraus: | + | *Nach Integration und Einsetzen der Grenzen folgt daraus: |
| − | $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$ | + | :$${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$ |
| − | $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega }\left( {1 - \cos ( {\omega T} )} \right).$$ | + | :$${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$ |
| − | Für die Frequenz $f = 1/(2T) = 10$ | + | *Für die Frequenz $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ erhält man: |
| − | $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$ | + | :$${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$ |
| + | |||
| + | :$${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | |||
| − | '''2 | + | '''(2)''' Das Betragsquadrat ist die Summe von Real- und Imaginärteil, jeweils quadriert: |
| − | $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\ | + | :$$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$ |
| − | Wegen $\sin^2(\alpha) + \cos^2(\alpha) = 1$ kann hierfür auch geschrieben werden: | + | *Wegen $\sin^2(\alpha) + \cos^2(\alpha) = 1$ kann hierfür auch geschrieben werden: |
| − | $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }}\ | + | :$$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$ |
| − | Setzt man für $\omega = 2\pi f$ und zieht die Wurzel, so erhält man unter der Voraussetzung $A > 0$: | + | *Setzt man für $\omega = 2\pi f$ und zieht die Wurzel, so erhält man unter der Voraussetzung $A > 0$: |
| − | $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$ | + | :$$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$ |
| − | Mit der Abkürzung $\text{si}(x) = \sin(x)/x$ lautet das Ergebnis: | + | *Mit der Abkürzung $\text{si}(x) = \sin(x)/x$ lautet das Ergebnis: |
| − | $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$ | + | :$$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$ |
| − | Der Spektralwert bei der Frequenz $f = 1/T = 20$ | + | *Der Spektralwert bei der Frequenz $f = 1/T = \text{20 kHz}$ ergibt sich zu |
| − | $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$ | + | :$$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$ |
| − | Bei der Berechnung des | + | *Bei der Berechnung des Wertes für $f = 0$ erscheint der Quotient $\text{0 durch 0}$. Durch Anwendung der [https://de.wikipedia.org/wiki/Regel_von_de_l%E2%80%99Hospital l'Hospitalschen Regel] kann der Grenzwert berechnet werden: |
| − | $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$ | + | :$$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$ |
| − | Daraus folgt: | + | *Daraus folgt: |
| − | $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= | + | :$$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$ |
| − | Dieses Ergebnis ist einsichtig, da nach dem ersten Fourierintegral der Spektralwert bei $f = 0$ genau der Fläche unter der Zeitfunktion entspricht. | + | *Dieses Ergebnis ist einsichtig, da nach dem ersten Fourierintegral der Spektralwert bei $f = 0$ genau der Fläche unter der Zeitfunktion entspricht. |
| − | |||
| − | '''3 | + | |
| − | Bei den Argumenten $f \cdot T | + | [[Datei:P_ID563__Sig_A_3_3_c.png|right|frame|Betragsspektrum des Rechteckimpulses]] |
| + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
| + | *Entsprechend dem Ergebnis zur Teilaufgabe '''(2)''' treten die Nullstellen im Abstand $f_0 = 1/T$ auf. | ||
| + | *Bei $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ ist zwar der Realteil $0$, aber nicht der Imaginärteil. | ||
| + | *Bei den Argumenten $f \cdot T = 0.5,\ 1.5,\ 2.5,\hspace{0.05cm}\text{ ... }$ ist die Sinusfunktion jeweils betragsmäßig gleich $1$, und es gilt: | ||
| − | $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$ | + | :$$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$ |
| + | |||
| + | *Bei anderen Frequenzen dient $X_{\rm S}(f)$ als obere Schranke, das heißt, es gilt stets $|Xf)| \leq X_{\rm S}(f)$. | ||
| + | *In der Skizze ist diese Schranke zusätzlich zu $|X(f)|$ als violette Kurve eingezeichnet. | ||
| + | |||
| − | |||
| − | |||
| − | '''4 | + | '''(4)''' Nach der Definition auf der Angabenseite kann man die Phasenfunktion wie folgt berechnen: |
| − | $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$ | + | :$$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$ |
| − | Mit den Ergebnissen aus Teilaufgabe 1 | + | *Mit den Ergebnissen aus Teilaufgabe '''(1)''' gilt somit: |
| − | $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$ | + | :$$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$ |
| − | Das Argument dieser Funktion ist entsprechend der Angabe gleich $\tan(\omega T/2) = \tan(\pi fT)$. Daraus folgt ein mit der Frequenz linear ansteigender Verlauf: | + | *Das Argument dieser Funktion ist entsprechend der Angabe gleich $\tan(\omega T/2) = \tan(\pi fT)$. Daraus folgt ein mit der Frequenz linear ansteigender Verlauf: |
| − | $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$ | + | :$$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$ |
| − | Mit $f = 10$ | + | *Mit $f = 10\,\text{kHz}$ und $T = 50\,\text{µs}$ erhält man daraus den Phasenwinkel $\pi /2$ entsprechend $\underline{90^{\circ}}$ . |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Aktuelle Version vom 23. April 2021, 09:46 Uhr
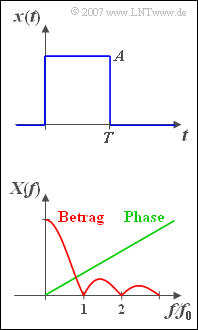
Betrachtet wird ein Rechteckimpuls $x(t)$ der Dauer $T = 50\,\text{µs}$ und der Höhe $A = 2\,\text{V}$. An den Sprungstellen bei $t = 0$ und $t = T$ ist der Signalwert jeweils $A/2$, was aber für die Lösung der Aufgabe keinen Einfluss hat.
In der unteren Grafik ist die dazugehörige Spektralfunktion nach Betrag und Phase qualitativ skizziert. Es gilt:
- $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$
Der analytische Funktionsverlauf von $X(f)$ soll ermittelt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Sonderfälle impulsartiger Signale.
- Gegeben sind weiterhin folgende trigonometrischen Umformungen:
- $$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$
Fragebogen
Musterlösung
(1) Mit der Abkürzung $\omega = 2\pi f$ lautet die Spektralfunktion gemäß dem ersten Fourierintegral:
- $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$
- Nach Integration und Einsetzen der Grenzen folgt daraus:
- $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$
- $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$
- Für die Frequenz $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ erhält man:
- $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$
- $${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) Das Betragsquadrat ist die Summe von Real- und Imaginärteil, jeweils quadriert:
- $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$
- Wegen $\sin^2(\alpha) + \cos^2(\alpha) = 1$ kann hierfür auch geschrieben werden:
- $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$
- Setzt man für $\omega = 2\pi f$ und zieht die Wurzel, so erhält man unter der Voraussetzung $A > 0$:
- $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$
- Mit der Abkürzung $\text{si}(x) = \sin(x)/x$ lautet das Ergebnis:
- $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$
- Der Spektralwert bei der Frequenz $f = 1/T = \text{20 kHz}$ ergibt sich zu
- $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$
- Bei der Berechnung des Wertes für $f = 0$ erscheint der Quotient $\text{0 durch 0}$. Durch Anwendung der l'Hospitalschen Regel kann der Grenzwert berechnet werden:
- $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$
- Daraus folgt:
- $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$
- Dieses Ergebnis ist einsichtig, da nach dem ersten Fourierintegral der Spektralwert bei $f = 0$ genau der Fläche unter der Zeitfunktion entspricht.
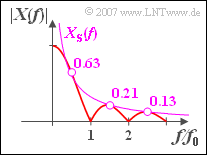
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Entsprechend dem Ergebnis zur Teilaufgabe (2) treten die Nullstellen im Abstand $f_0 = 1/T$ auf.
- Bei $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ ist zwar der Realteil $0$, aber nicht der Imaginärteil.
- Bei den Argumenten $f \cdot T = 0.5,\ 1.5,\ 2.5,\hspace{0.05cm}\text{ ... }$ ist die Sinusfunktion jeweils betragsmäßig gleich $1$, und es gilt:
- $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$
- Bei anderen Frequenzen dient $X_{\rm S}(f)$ als obere Schranke, das heißt, es gilt stets $|Xf)| \leq X_{\rm S}(f)$.
- In der Skizze ist diese Schranke zusätzlich zu $|X(f)|$ als violette Kurve eingezeichnet.
(4) Nach der Definition auf der Angabenseite kann man die Phasenfunktion wie folgt berechnen:
- $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$
- Mit den Ergebnissen aus Teilaufgabe (1) gilt somit:
- $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$
- Das Argument dieser Funktion ist entsprechend der Angabe gleich $\tan(\omega T/2) = \tan(\pi fT)$. Daraus folgt ein mit der Frequenz linear ansteigender Verlauf:
- $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$
- Mit $f = 10\,\text{kHz}$ und $T = 50\,\text{µs}$ erhält man daraus den Phasenwinkel $\pi /2$ entsprechend $\underline{90^{\circ}}$ .