Kanalcodierung/Algebraische und polynomische Beschreibung: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
|||
| (61 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| − | == | + | == Aufteilung der Generatormatrix in Teilmatrizen == |
<br> | <br> | ||
| − | Entsprechend den Ausführungen | + | Entsprechend den Ausführungen im früheren Abschnitt [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Lineare_Codes_und_zyklische_Codes| Lineare Codes und zyklische Codes]] lässt sich das Codewort $\underline{x}$ eines linearen Blockcodes aus dem Informationswort $\underline{u}$ und der Generatormatrix $\mathbf{G}$ in einfacher Weise ermitteln: $\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}}$. Dabei gilt: |
| + | *Die Vektoren $\underline{u}$ und $\underline{x}$ haben die Länge $k$ (Bitanzahl eines Informationswortes) bzw. $n$ (Bitanzahl eines Codewortes) und $\mathbf{G}$ besitzt die Dimension $k × n$ $(k$ Zeilen und $n$ Spalten$)$.<br> | ||
| − | + | *Bei Faltungscodierung bezeichnen dagegen $\underline{u}$ und $\underline{x}$ Sequenzen mit $k\hspace{0.05cm}' → ∞$ und $n\hspace{0.05cm}' → ∞$. Deshalb wird auch die Generatormatrix $\mathbf{G}$ in beiden Richtungen unendlich weit ausgedehnt sein.<br><br> | |
| − | + | Als Vorbereitung für die Einführung der Generatormatrix $\mathbf{G}$ auf der nächsten Seite definieren wir $m + 1$ Teilmatrizen, jeweils mit $k$ Zeilen und $n$ Spalten, die wir mit $\mathbf{G}_l$ bezeichnen, wobei $0 ≤ l ≤ m$ gilt.<br> | |
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Definition:}$ Die '''Teilmatrix''' $\mathbf{G}_l$ beschreibt folgenden Sachverhalt: Ist das Matrixelement $\mathbf{G}_l(\kappa, j) = 1$, so sagt dies aus, dass das Codebit $x_i^{(j)}$ durch das Informationsbit $u_{i-l}^{(\kappa)}$ beeinflusst wird. Andernfalls ist dieses Matrixelement gleich $0$.}}<br> | |
| − | |||
| − | |||
| − | { | ||
Diese Definition wird nun an einem Beispiel verdeutlicht. | Diese Definition wird nun an einem Beispiel verdeutlicht. | ||
| − | + | [[Datei:P ID2600 KC T 3 1 S4 v1.png|right|frame|Faltungscoder mit $k = 2, \ n = 3, \ m = 1$]] | |
| − | [[Datei:P ID2600 KC T 3 1 S4 v1.png| | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 1:}$ | ||
| + | Wir betrachten wiederum den Faltungscodierer gemäß der Grafik mit folgenden Codebits: | ||
| − | :<math>x_i^{(1)} | + | ::<math>x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},</math> |
| − | :<math>x_i^{(2)} | + | ::<math>x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},</math> |
| − | :<math>x_i^{(3)} | + | ::<math>x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.</math> |
| − | Wegen der Gedächtnisordnung | + | Wegen der Gedächtnisordnung $m = 1$ wird dieser Codierer durch die beiden Teilmatrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ vollständig charakterisiert: |
| − | :<math>{ \boldsymbol{\rm G}}_0 = | + | ::<math>{ \boldsymbol{\rm G} }_0 = |
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 0 & 1\\ | 1 & 0 & 1\\ | ||
0 & 1 & 1 | 0 & 1 & 1 | ||
\end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} | \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} | ||
| − | { \boldsymbol{\rm G}}_1 = \begin{pmatrix} | + | { \boldsymbol{\rm G} }_1 = \begin{pmatrix} |
1 & 1 & 1\\ | 1 & 1 & 1\\ | ||
1 & 0 & 0 | 1 & 0 & 0 | ||
| Zeile 43: | Zeile 42: | ||
Diese Matrizen sind wie folgt zu interpretieren: | Diese Matrizen sind wie folgt zu interpretieren: | ||
| − | *Erste Zeile von | + | *Erste Zeile von $\mathbf{G}_0$, rote Pfeile: $\hspace{1.1cm}u_i^{(1)}$ beeinflusst sowohl $x_i^{(1)}$ als auch $x_i^{(3)}$, nicht jedoch $x_i^{(2)}$.<br> |
| − | *Zweite Zeile von | + | *Zweite Zeile von $\mathbf{G}_0$, blaue Pfeile: $\hspace{0.6cm}u_i^{(2)}$ beeinflusst $x_i^{(2)}$ und $x_i^{(3)}$, aber nicht $x_i^{(1)}$.<br> |
| − | *Erste Zeile von | + | *Erste Zeile von $\mathbf{G}_1$, grüne Pfeile: $\hspace{0.9cm}u_{i-1}^{(1)}$ beeinflusst alle drei Coderausgänge.<br> |
| − | *Zweite Zeile von | + | *Zweite Zeile von $\mathbf{G}_1$, brauner Pfeil: $\hspace{0.45cm}u_{i-1}^{(2)}$ beeinflusst nur $x_i^{(1)}$.}}<br> |
| − | == Generatormatrix eines Faltungscodierers mit Gedächtnis m == | + | == Generatormatrix eines Faltungscodierers mit Gedächtnis ''m'' == |
<br> | <br> | ||
| − | Mit den Teilmatrizen | + | Mit den Teilmatrizen $\mathbf{G}_0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \mathbf{G}_m$ lassen sich die $n$ Codebits zum Zeitpunkt $i$ wie folgt ausdrücken: |
| − | :<math>\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = | + | ::<math>\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = |
| − | \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 + ... + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m | + | \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 +\hspace{0.05cm} \text{...} \hspace{0.05cm} + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
Hierbei sind folgende vektorielle Größen zu berücksichtigen: | Hierbei sind folgende vektorielle Größen zu berücksichtigen: | ||
| − | :<math>\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} | + | ::<math>\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} |
| − | \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.</math> | + | \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.</math> |
| − | Betrachtet man die bei | + | Betrachtet man die bei $i = 1$ beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen |
| − | :<math>\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} | + | ::<math>\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} |
| − | \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},</math> | + | \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm} \big)\hspace{0.05cm},</math> |
| − | so kann dieser Zusammenhang durch die Matrixgleichung | + | so kann dieser Zusammenhang durch die Matrixgleichung $\underline{x} = \underline{u} \cdot \mathbf{G}$ ausgedrückt werden. Hierbei ist für die Generatormatrix $\mathbf{G}$ wie folgt zu setzen: |
| − | :<math>{ \boldsymbol{\rm G}}=\begin{pmatrix} | + | ::<math>{ \boldsymbol{\rm G}}=\begin{pmatrix} |
{ \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ | ||
& { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ | & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ | ||
| Zeile 78: | Zeile 77: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Aus der Gleichung erkennt man sofort das Gedächtnis | + | *Aus der Gleichung erkennt man sofort das Gedächtnis $m$ des Faltungscodes. Die Parameter $k$ und $n$ sind direkt nicht ablesbar. |
| + | * Sie sind aber durch die Zeilen– und Spaltenanzahl der Teilmatrizen $\mathbf{G}_l$ festgelegt.<br> | ||
| + | |||
| − | + | [[Datei:P ID2601 KC T 3 2 S2 v1.png|right|frame|Generatormatrix eines Faltungscodes]] | |
| − | [[Datei:P ID2601 KC T 3 2 S2 v1.png| | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 2:}$ | ||
| + | Mit den zwei Matrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ – siehe [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Aufteilung_der_Generatormatrix_in_Teilmatrizen| $\text{Beispiel 1}$]] – erhält man die rechts skizzierte Matrix $\mathbf{G}$. | ||
Anzumerken ist: | Anzumerken ist: | ||
| − | *Die Generatormatrix | + | *Die Generatormatrix $\mathbf{G}$ erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur acht Zeilen und zwölf Spalten. |
| − | |||
| − | |||
| − | * | + | *Für die zeitlich begrenzte Informationssequenz $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1)$ ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann: |
| + | :$$\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0).$$ | ||
| − | :: | + | *Anhand der Beschriftungsfarben lassen sich die $n = 3$ Codewortstränge ablesen. |
| − | \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}. | + | *Das gleiche Ergebnis haben wir (auf anderem Wege) im [[Kanalcodierung/Grundlagen_der_Faltungscodierung#Faltungscodierer_mit_zwei_Eing.C3.A4ngen| $\text{Beispiel 4}$]] am Ende des letzten Kapitels erhalten: |
| + | :$$\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} | ||
| + | \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} | ||
| + | \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.$$}}<br> | ||
| − | == Generatormatrix für Faltungscodierer der Rate 1/n == | + | == Generatormatrix für Faltungscodierer der Rate 1/''n'' == |
<br> | <br> | ||
| − | Wir betrachten nun den Sonderfall | + | Wir betrachten nun den Sonderfall $k = 1$, |
| + | *zum einen aus Gründen einer möglichst einfachen Darstellung, | ||
| + | *aber auch, weil Faltungscodierer der Rate $1/n$ für die Praxis eine große Bedeutung besitzen.<br><br> | ||
| − | [[Datei:P ID2602 KC T 3 2 S3a.png| | + | [[Datei:P ID2602 KC T 3 2 S3a.png|right|frame|Faltungscoder mit $k = 1, \ n = 2, \ m = 1$]] |
| + | <b>Faltungscodierer mit $k = 1, \ n = 2, \ m = 1$</b><br> | ||
| − | + | Aus nebenstehender Skizze kann abgeleitet werden: | |
| − | + | ::<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | |
| − | |||
| − | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
1 & 1 | 1 & 1 | ||
\end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
{ \boldsymbol{\rm G}}_1=\begin{pmatrix} | { \boldsymbol{\rm G}}_1=\begin{pmatrix} | ||
0 & 1 | 0 & 1 | ||
| − | \end{pmatrix} | + | \end{pmatrix}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
| − | |||
| − | |||
{ \boldsymbol{\rm G}}=\begin{pmatrix} | { \boldsymbol{\rm G}}=\begin{pmatrix} | ||
11 & 01 & 00 & 00 & 00 & \cdots & \\ | 11 & 01 & 00 & 00 & 00 & \cdots & \\ | ||
| Zeile 119: | Zeile 123: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Für die Eingangssequenz | + | Für die Eingangssequenz $\underline{u} = (1, 0, 1, 1)$ beginnt die Codesequenz mit $\underline{x} = (1, 1, 0, 1, 1, 1, 1, 0, \ \text{...})$. <br>Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Generatormatrix.<br><br> |
| − | [[Datei:P ID2603 KC T 3 2 S3b.png| | + | [[Datei:P ID2603 KC T 3 2 S3b.png|right|frame|Faltungscoder mit $k = 1, \ n = 2, \ m = 2$]] |
| + | <b>Faltungscodierer mit $k = 1, \ n = 2, \ m = 2$</b><br> | ||
| − | + | Aufgrund der Gedächtnisordnung $m = 2$ gibt es hier drei Teilmatrizen: | |
| − | + | ::<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | |
| − | |||
| − | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
1 & 1 | 1 & 1 | ||
\end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| Zeile 137: | Zeile 140: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | :<math> | + | Damit lautet die resultierende Generatormatrix: |
| − | + | ||
| + | ::<math> { \boldsymbol{\rm G}}=\begin{pmatrix} | ||
11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ | 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ | ||
00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ | 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ | ||
| Zeile 146: | Zeile 150: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Hier führt die Eingangsssequenz | + | Hier führt die Eingangsssequenz $\underline{u} = (1, 0, 1, 1)$ zur Codesequenz $\underline{x} = (1, 1, 1, 0, 0, 0, 0, 1, \ \text{...})$.<br><br> |
| − | [[Datei:P ID2604 KC T 3 2 S3c.png| | + | [[Datei:P ID2604 KC T 3 2 S3c.png|right|frame|Faltungscoder mit $k = 1, \ n = 3, \ m = 3$]] |
| + | <b>Faltungscodierer mit $k = 1, \ n = 3, \ m = 3$</b> | ||
| − | + | Wegen $m = 3$ gibt es nun vier Teilmatrizen der jeweiligen Dimension $1 × 3$: | |
| − | + | ::<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | |
| − | |||
| − | :<math>{ \boldsymbol{\rm G}}_0=\begin{pmatrix} | ||
1 & 1 & 0 | 1 & 1 & 0 | ||
\end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
{ \boldsymbol{\rm G}}_1=\begin{pmatrix} | { \boldsymbol{\rm G}}_1=\begin{pmatrix} | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
| − | \end{pmatrix}\hspace{0.05cm}, | + | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} |
| − | + | { \boldsymbol{\rm G}}_2=\begin{pmatrix} | |
| − | |||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} | ||
| Zeile 170: | Zeile 172: | ||
Damit lautet die resultierende Generatormatrix: | Damit lautet die resultierende Generatormatrix: | ||
| − | :<math>{ \boldsymbol{\rm G}}=\begin{pmatrix} | + | ::<math>{ \boldsymbol{\rm G}}=\begin{pmatrix} |
110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ | 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ | ||
000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ | 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ | ||
| Zeile 178: | Zeile 180: | ||
\end{pmatrix}\hspace{0.05cm},</math> | \end{pmatrix}\hspace{0.05cm},</math> | ||
| − | und man erhält für | + | und man erhält für $\underline{u} = (1, 0, 1, 1)$ die Codesequenz $\underline{x} = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, \ \text{...})$.<br> |
| − | == GF(2)–Beschreibungsformen eines Digitalen Filters | + | == GF(2)–Beschreibungsformen eines Digitalen Filters == |
<br> | <br> | ||
| − | + | [[Datei:P ID2605 KC T 3 2 S4 v1.png|right|frame|Digitales Filter in ${\rm GF}(2)$ der Ordnung $m$|class=fit]] | |
| + | Im Kapitel [[Kanalcodierung/Grundlagen_der_Faltungscodierung#Rate.E2.80.931.2F2.E2.80.93Faltungscodierer_.282.29| Grundlagen der Faltungscodierung]] wurde bereits darauf hingewiesen, | ||
| + | *dass ein Rate $1/n$–Faltungscodierer durch mehrere Digitale Filter realisiert werden kann, | ||
| + | *wobei die Filter parallel mit der gleichen Eingangsfolge $\underline{u}$ arbeiten. | ||
| + | |||
| + | |||
| + | Bevor wir diese Aussage vertiefen, sollen zuerst die Eigenschaften eines Digitalfilters für das Galoisfeld ${\rm GF(2)}$ genannt werden. | ||
| − | |||
Die Grafik ist wie folgt zu interpretieren: | Die Grafik ist wie folgt zu interpretieren: | ||
| − | *Das Filter besitzt die Impulsantwort | + | *Das Filter besitzt die Impulsantwort $\underline{g} = (g_0, g_1, g_2, \ \text{...} \ , g_m)$. |
| + | * Für alle Filterkoeffizienten $($mit den Indizes $0 ≤ l ≤ m)$ gilt: $g_l ∈ {\rm GF}(2) = \{0, 1\}$.<br> | ||
| − | *Die einzelnen Symbole | + | *Die einzelnen Symbole $u_i$ der Eingangsfolge $\underline{u}$ seien ebenfalls binär: $u_i ∈ \{0, 1\}$. |
| + | *Damit gilt für das Ausgangssymbol zu den Zeitpunkten $i ≥ 1$ mit Addition und Multiplikation in ${\rm GF(2)}$: | ||
::<math>x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.</math> | ::<math>x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.</math> | ||
| − | *Dies entspricht der (zeitdiskreten) [ | + | *Dies entspricht der (zeitdiskreten) [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Faltung_im_Zeitbereich| Faltungsoperation]] (englisch: <i>Convolution</i> ), gekennzeichnet durch einen Stern. Damit kann für die gesamte Ausgangssequenz geschrieben werden: |
::<math>\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.</math> | ::<math>\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.</math> | ||
| − | *Wesentlicher Unterschied gegenüber dem [ | + | *Wesentlicher Unterschied gegenüber dem Kapitel [[Stochastische_Signaltheorie/Digitale_Filter| Digitale Filter]] im Buch „Stochastische Signaltheorie” ist die Modulo–2–Addition $(1 + 1 = 0)$ anstelle der herkömmlichen Addition $(1 + 1 = 2)$.<br><br> |
| − | + | [[Datei:P ID2606 KC T 3 2 S4b.png|right|frame|Digitales Filter mit Impulsantwort $(1, 0, 1, 1)$]] | |
| − | [[Datei:P ID2606 KC T 3 2 S4b.png| | + | {{GraueBox|TEXT= |
| − | Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt: | + | $\text{Beispiel 3:}$ |
| + | Die Impulsantwort des dargestellten Digitalen Filters dritter Ordnung lautet: $\underline{g} = (1, 0, 1, 1)$. | ||
| + | *Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt: $\underline{u} = (1, 1, 0, 0, 0, \ \text{ ...})$.<br> | ||
| − | Damit ergibt sich die (unendliche) Ausgangssequenz | + | *Damit ergibt sich die (unendliche) Ausgangssequenz $\underline{x}$ im binären Galoisfeld ⇒ ${\rm GF(2)}$: |
| − | :<math>\underline{x} | + | ::<math>\underline{x} = (\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1\hspace{0.05cm})</math> |
| − | :<math>\hspace{0.3cm} | + | ::<math>\Rightarrow \hspace{0.3cm} \underline{x} =(\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}0,\hspace{0.05cm} \text{ ...} \hspace{0.05cm}) |
| − | \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} . ... \hspace{0.05cm}) | + | \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} \hspace{0.05cm} \text{ ...}\hspace{0.05cm}) |
| − | = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.</math> | + | = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.</math> |
| − | Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet: | + | *Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet: |
| − | :<math>\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . .. | + | ::<math>\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.</math>}}<br> |
| − | + | Zeitdiskrete Signale kann man aber auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.<br> | |
| − | |||
| − | Zeitdiskrete Signale kann man auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.<br> | ||
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ Die zum zeitdiskreten Signal $\underline{x} = (x_0, x_1, x_2, \ \text{...})$ gehörige $D$<b>–Transformierte</b> lautet: | ||
| − | :<math>X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}...\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.</math> | + | ::<math>X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}\text{...}\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.</math> |
| − | Für diese spezielle Transformation in einen Bildbereich verwenden wir auch | + | Für diese spezielle Transformation in einen Bildbereich verwenden wir auch folgende Notation, wobei „$D$” für ''Delay Operator'' steht: |
| − | :<math>\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad | + | ::<math>\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad |
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
| − | X(D) = \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.</math> | + | X(D) = \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.</math>}}<br> |
| − | In der Literatur wird manchmal | + | ''Hinweis'': In der Literatur wird manchmal $x(D)$ anstelle von $X(D)$ verwendet. Wir schreiben in unserem Lerntutorial aber alle Bildbereichsfunktionen mit Großbuchstaben, zum Beispiel die Fourier–, die Laplace– und die $D$–Transformation: |
| − | :<math>x(t) \hspace{0.15cm} | + | ::<math>x(t) \hspace{0.15cm} |
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} | ||
X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} | X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} | ||
| Zeile 238: | Zeile 248: | ||
X(D) \hspace{0.05cm}.</math> | X(D) \hspace{0.05cm}.</math> | ||
| − | |||
| − | :<math>\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad | + | Wir wenden nun die $D$–Transformation auch auf die Informationssequenz $\underline{u}$ und die Impulsantwort $\underline{g}$ an. Aufgrund der zeitlichen Begrenzung von $\underline{g}$ ergibt sich die obere Summationsgrenze bei $G(D)$ zu $i = m$:<br> |
| + | |||
| + | ::<math>\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}\text{...}\hspace{0.05cm}) \quad | ||
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
| − | U(D) = \sum_{i = 0}^{\infty} u_i \cdot D^i \hspace{0.05cm},</math> | + | U(D) = \sum_{i = 0}^{\infty} u_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm},</math> |
| − | :<math>\underline{g} = (g_0, g_1, \hspace{0.05cm}...\hspace{0.05cm}, g_m) \quad | + | ::<math>\underline{g} = (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, g_m) \quad |
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
| − | G(D) = \sum_{i = 0}^{m} g_i \cdot D^i \hspace{0.05cm}.</math | + | G(D) = \sum_{i = 0}^{m} g_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.</math> |
| − | {{Satz} | + | {{BlaueBox|TEXT= |
| + | $\text{Satz:}$ Wie bei allen Spektraltransformationen gilt auch bei der $D$–Transformation im Bildbereich die <b>Multiplikation</b>, da die (diskreten) Zeitsignale $\underline{u}$ und $\underline{g}$ durch die <b>Faltung</b> verknüpft sind: | ||
| − | :<math>\underline{x} = \underline{u} * \underline{g} \quad | + | ::<math>\underline{x} = \underline{u} * \underline{g} \quad |
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
X(D) = U(D) \cdot G(D) \hspace{0.05cm}.</math> | X(D) = U(D) \cdot G(D) \hspace{0.05cm}.</math> | ||
| − | Man bezeichnet | + | Man bezeichnet – wie in der [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang| Systemtheorie]] allgemein üblich – auch die $D$–Transformierte $G(D)$ der Impulsantwort $\underline{g}$ als '''Übertragungsfunktion''' (englisch: <i>Transfer Function</i>). Der (recht einfache) $\rm Beweis$ dieses wichtigen Ergebnisses finden Sie in der Angabe zur [[Aufgaben:3.3Z_Faltung_und_D%E2%80%93Transformation|Aufgabe 3.3Z]].}}<br> |
| − | + | [[Datei:P ID2607 KC T 3 2 S4b.png|right|frame|Digitales Filter mit Impulsantwort $(1, 0, 1, 1)$]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ Wir betrachten wieder die zeitdiskreten Signale | ||
| − | + | ::<math>\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \quad | |
| − | |||
| − | |||
| − | :<math>\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}...\hspace{0.05cm}) \quad | ||
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
U(D) = 1+ D \hspace{0.05cm},</math> | U(D) = 1+ D \hspace{0.05cm},</math> | ||
| − | :<math>\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad | + | ::<math>\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad |
\circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | ||
G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.</math> | G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.</math> | ||
| − | Wie im | + | Wie im $\text{Beispiel 3}$ (auf dieser Seite oben) erhält man auch auf diesem Lösungsweg: |
| − | :<math>X(D) | + | ::<math>X(D) = U(D) \cdot G(D) = (1+D) \cdot (1+ D^2 + D^3) </math> |
| − | :<math>\ | + | ::<math>\Rightarrow \hspace{0.3cm} X(D) = 1+ D^2 + D^3 +D + D^3 + D^4 = 1+ D + D^2 + D^4 \hspace{0.3cm} |
| + | \Rightarrow \hspace{0.3cm} \underline{x} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \text{...} \hspace{0.05cm}) \hspace{0.05cm}.</math> | ||
| − | :< | + | Die Multiplikation mit $D$ im Bildbereich entspricht im Zeitbereich einer Verschiebung um eine Stelle nach rechts, weshalb man $D$ als <i>Verzögerungsoperator</i> (englisch: <i>Delay Operator</i> ) bezeichnet: |
| − | + | ::<math>W(D) = D \cdot X(D) \quad | |
| − | |||
| − | :<math>W(D) = D \cdot X(D) \quad | ||
\bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad | \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad | ||
| − | \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.</math> | + | \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \text{...} \hspace{0.05cm}) \hspace{0.05cm}.</math>}}<br> |
| − | == Anwendung der D–Transformation auf Rate–1/ | + | == Anwendung der D–Transformation auf Rate–1/''n''–Faltungscoder == |
<br> | <br> | ||
| − | Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall | + | Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall $k = 1$ beschränken. |
| + | *Ein solcher $(n, \ k = 1)$–Faltungscode lässt sich mit $n$ Digitalen Filtern realisieren, die auf der gleichen Informationssequenz $\underline{u}$ parallel arbeiten. | ||
| + | *Die Grafik zeigt die Anordnung für den Codeparameter $n = 2$ ⇒ Coderate $R = 1/2$.<br> | ||
| − | |||
| − | + | [[Datei:P ID2608 KC T 3 2 S5 v1.png|center|frame|Zwei parallel arbeitende Filter, jeweils mit Ordnung $m$|class=fit]] | |
| − | |||
| − | + | Die folgenden Gleichungen gelten für beide Filter gleichermaßen, wobei für das obere Filter $j = 1$ und für das untere Filter $j = 2$ zu setzen ist: | |
| + | *Die <b>Impulsantworten</b> der beiden Filter ergeben sich zu | ||
| − | + | ::<math>\underline{g}^{(j)} = (g_0^{(j)}, g_1^{(j)}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, g_m^{(j)}\hspace{0.01cm}) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.</math> | |
| − | + | *Die zwei <b>Ausgangssequenzen</b> lauten, wobei berücksichtigt ist, dass beide Filter auf der gleichen Eingangssequenz $\underline{u} = (u_0, u_1, u_2, \hspace{0.05cm} \text{...})$ arbeiten: | |
| − | : | + | ::<math>\underline{x}^{(j)} = (x_0^{(j)}, x_1^{(j)}, x_2^{(j)}, \hspace{0.05cm}\text{...}\hspace{0.05cm}) = \underline{u} \cdot \underline{g}^{(j)} \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.</math> |
| − | *Für die <b | + | *Für die $D$<b>–Transformierten</b> der Ausgangssequenzen gilt: |
::<math>X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.</math> | ::<math>X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.</math> | ||
| − | + | Um diesen Sachverhalt kompakter darstellen zu können, definieren wir nun folgende vektorielle Größen eines Faltungscodes der Rate $1/n$: | |
| − | = | + | {{BlaueBox|TEXT= |
| − | < | + | $\text{Definition:}$ Die $D$<b>–Übertragungsfunktionen</b> der $n$ parallel angeordneten Digitalen Filter werden im Vektor $\underline{G}(D)$ zusammengefasst: |
| − | |||
| − | {{ | + | ::<math>\underline{G}(D) = \left ( G^{(1)}(D), G^{(2)}(D), \hspace{0.05cm}\text{...}\hspace{0.1cm}, G^{(n)} (D) \right )\hspace{0.05cm}.</math> |
| − | + | *Der Vektor $\underline{X}(D)$ beinhaltet die $D$<b>–Transformierten</b> der $n$ Codesequenzen $\underline{x}^{(1)}, \underline{x}^{(2)}, \ \text{...} \ , \underline{x}^{(n)}$: | |
| − | + | ::<math>\underline{X}(D) = \left ( X^{(1)}(D), X^{(2)}(D), \hspace{0.05cm}\text{...}\hspace{0.1cm}, X^{(n)} (D) \right )\hspace{0.05cm}.</math> | |
| − | : | + | *Damit erhält man die folgende Vektorgleichung: |
| − | + | ::<math>\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.</math> | |
| − | + | *Aufgrund des Codeparameters $k = 1$ ist $U(D)$ hier keine vektorielle Größe.}}<br> | |
| − | + | [[Datei:P ID2609 KC T 3 2 S5b.png|right|frame|Faltungscoder mit $n = 2, \ k = 1,\ m = 2$]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 5:}$ | ||
| + | Wir betrachten den Faltungscodierer mit den Codeparametern $n = 2, \ k = 1, \ m = 2$. Für diesen gilt: | ||
| − | + | ::<math>\underline{g}^{(1)} =(\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad | |
| − | |||
| − | |||
| − | :<math>\underline{g}^{(1)} | ||
G(D) = 1+ D + D^2 \hspace{0.05cm},</math> | G(D) = 1+ D + D^2 \hspace{0.05cm},</math> | ||
| − | :<math>\underline{g}^{(2)} | + | ::<math>\underline{g}^{(2)}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad |
G(D) = 1+ D^2 </math> | G(D) = 1+ D^2 </math> | ||
| + | ::<math>\Rightarrow \hspace{0.3cm} \underline{G}(D) = \big ( 1+ D + D^2 \hspace{0.05cm}, \hspace{0.1cm}1+ D^2 \big )\hspace{0.05cm}.</math> | ||
| − | + | Die Informationssequenz sei $\underline{u} = (1, 0, 1, 1)$ ⇒ $D$–Transformierte $U(D) = 1 + D^2 + D^3$. Damit erhält man: | |
| − | + | ::<math>\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}</math> | |
| − | |||
| − | :<math>\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}</math> | ||
wobei | wobei | ||
| − | :<math>{X}^{(1)}(D) | + | ::<math>{X}^{(1)}(D) = (1+ D^2 + D^3) \cdot (1+ D + D^2)=1+ D + D^2 + D^2 + D^3 + D^4 + D^3 + D^4 + D^5 = 1+ D + D^5</math> |
| − | |||
| − | :<math>\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},</math> | + | ::<math>\Rightarrow \hspace{0.3cm} \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},</math> |
| − | :<math>{X}^{(2)}(D) | + | ::<math>{X}^{(2)}(D) = (1+ D^2 + D^3) \cdot (1+ D^2)=1+ D^2 + D^2 + D^4 + D^3 + D^5 = 1+ D^3 + D^4 + D^5</math> |
| − | |||
| − | :<math>\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.</math> | + | ::<math>\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.</math> |
| − | Das gleiche Ergebnis haben wir in der Aufgabe | + | Das gleiche Ergebnis haben wir in der [[Aufgaben:3.1Z_Faltungscodes_der_Rate_1/2|Aufgabe 3.1Z]] auf anderem Wege erhalten. Nach dem Multplexen der beiden Stränge erhält man wieder: |
| + | :$$\underline{x} = (11, 10, 00, 01, 01, 11, 00, 00, \hspace{0.05cm} \text{...} \hspace{0.05cm}).$$}}<br> | ||
| − | == Übertragungsfunktionsmatrix – Transfer Function Matrix | + | == Übertragungsfunktionsmatrix – Transfer Function Matrix == |
<br> | <br> | ||
| − | + | [[Datei:P ID2616 KC T 3 2 S6b v1.png|right|frame|Allgemeiner $(n, \ k)$–Faltungscoder |class=fit]] | |
| − | + | Wir haben gesehen, dass ein Faltungscode der Rate $1/n$ sich am kompaktesten als Vektorgleichung im $D$–transformierten Bereich beschreiben lässt: $\underline{X}(D) = U(D) \cdot \underline{G}(D)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Nun erweitern wir das Resultat auf Faltungscodierer mit mehr als einem Eingang ⇒ $k ≥ 2$ (siehe Grafik).<br> | |
| − | + | Um einen Faltungscode der Rate $k/n$ im $D$–Bereich abbilden zu können, muss die Dimension obiger Vektorgleichung hinsichtlich Eingang und Übertragungsfunktion erhöht werden: | |
| − | + | ::<math>\underline{X}(D) = \underline{U}(D) \cdot { \boldsymbol{\rm G}}(D)\hspace{0.05cm}.</math> | |
| − | *Aus der skalaren Funktion | + | <br clear=all> |
| + | Dazu sind folgende Maßnahmen erforderlich: | ||
| + | *Aus der skalaren Funktion $U(D)$ wird der Vektor $\underline{U}(D) = (U^{(1)}(D), \ U^{(2)}(D), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ U^{(k)}(D))$.<br> | ||
| − | *Aus dem Vektor | + | *Aus dem Vektor $\underline{G}(D)$ wird die $k × n$–'''Übertragungsfunktionsmatrix''' $\mathbf{G}(D)$ (englisch: <i>Transfer Function Matrix</i> oder <i>Polynomial Generator Matrix</i>): |
::<math>{\boldsymbol{\rm G}}(D)=\begin{pmatrix} | ::<math>{\boldsymbol{\rm G}}(D)=\begin{pmatrix} | ||
| − | G_1^{(1)}(D) & G_1^{(2)}(D) & \ | + | G_1^{(1)}(D) & G_1^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_1^{(n)}(D)\\ |
| − | G_2^{(1)}(D) & G_2^{(2)}(D) & \ | + | G_2^{(1)}(D) & G_2^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_2^{(n)}(D)\\ |
\vdots & \vdots & & \vdots\\ | \vdots & \vdots & & \vdots\\ | ||
| − | G_k^{(1)}(D) & G_k^{(2)}(D) & \ | + | G_k^{(1)}(D) & G_k^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_k^{(n)}(D) |
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | *Jedes der | + | *Jedes der $k \cdot n$ Matrixelemente $G_i^{(j)}(D)$ mit $1 ≤ i ≤ k,\ \ 1 ≤ j ≤ n$ ist ein Polynom über der Dummy–Variablen $D$ im Galoisfeld ${\rm GF}(2)$, maximal vom Grad $m$, wobei $m$ das Gedächtnis angibt.<br> |
| − | *Für die obige <i>Übertragungsfunktionsmatrix</i> kann mit den zu Beginn dieses Kapitels definierten [ | + | *Für die obige <i>Übertragungsfunktionsmatrix</i> kann mit den zu Beginn dieses Kapitels definierten [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Definition_und_Interpretation_der_Teilmatrizen_G0.2C_..._.2C_Gm| Teilmatrizen]] $\mathbf{G}_0, \ \text{...} \ , \mathbf{G}_m$ auch geschrieben werden $($als Index verwenden wir wieder $l)$: |
::<math>{\boldsymbol{\rm G}}(D) = \sum_{l = 0}^{m} {\boldsymbol{\rm G}}_l \cdot D\hspace{0.03cm}^l | ::<math>{\boldsymbol{\rm G}}(D) = \sum_{l = 0}^{m} {\boldsymbol{\rm G}}_l \cdot D\hspace{0.03cm}^l | ||
| − | = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D + {\boldsymbol{\rm G}}_2 \cdot D^2 + ... \hspace{0.05cm}+ {\boldsymbol{\rm G}}_m \cdot D\hspace{0.03cm}^m | + | = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D + {\boldsymbol{\rm G}}_2 \cdot D^2 + \hspace{0.05cm} \text{...} \hspace{0.05cm}+ {\boldsymbol{\rm G}}_m \cdot D\hspace{0.03cm}^m |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | [[Datei:P ID2617 KC T 3 1 S4 v1.png|right|frame|Faltungscoder mit $k = 2, \ n = 3, \ m = 1$]] | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 6:}$ | ||
| + | Wir betrachten den $(n = 3, \ k = 2, \ m = 1)$–Faltungscoder, dessen Teilmatrizen bereits im [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Aufteilung_der_Generatormatrix_in_Teilmatrizen| $\text{Beispiel 1}$]] wie folgt ermittelt wurden: | ||
| − | + | ::<math>{ \boldsymbol{\rm G} }_0 = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | :<math>{ \boldsymbol{\rm G}}_0 = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 0 & 1\\ | 1 & 0 & 1\\ | ||
0 & 1 & 1 | 0 & 1 & 1 | ||
| − | \end{pmatrix} \hspace{0.05cm}, \ | + | \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} |
| − | { \boldsymbol{\rm G}}_1 = \begin{pmatrix} | + | { \boldsymbol{\rm G} }_1 = \begin{pmatrix} |
1 & 1 & 1\\ | 1 & 1 & 1\\ | ||
1 & 0 & 0 | 1 & 0 & 0 | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Wegen | + | Wegen $m = 1$ existieren keine Teilmatrizen für $l ≥ 2$. Damit lautet die Übertragungsfunktionsmatrix: |
| − | :<math>{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D = | + | ::<math>{\boldsymbol{\rm G} }(D) = {\boldsymbol{\rm G} }_0 + {\boldsymbol{\rm G} }_1 \cdot D = |
\begin{pmatrix} | \begin{pmatrix} | ||
1+D & D & 1+D\\ | 1+D & D & 1+D\\ | ||
| Zeile 411: | Zeile 414: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Die (zeitlich begrenzte) Informationssequenz sei | + | Die (zeitlich begrenzte) Informationssequenz sei $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1)$, woraus sich die beiden Eingangsfolgen wie folgt ergeben: |
| − | :<math>\underline{u}^{(1)} | + | ::<math>\underline{u}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad |
{U}^{(1)}(D) = D + D^3 \hspace{0.05cm},</math> | {U}^{(1)}(D) = D + D^3 \hspace{0.05cm},</math> | ||
| − | :<math>\underline{u}^{(2)} | + | ::<math>\underline{u}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad |
{U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.</math> | {U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.</math> | ||
| − | Daraus folgt für den Vektor der | + | Daraus folgt für den Vektor der $D$–Transformierten am Coderausgang: |
| − | :<math>\underline{X}(D) | + | ::<math>\underline{X}(D) = \big (\hspace{0.05cm} {X}^{(1)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(2)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(3)}(D)\hspace{0.05cm}\big ) = \underline{U}(D) \cdot {\boldsymbol{\rm G} }(D) |
| − | + | \begin{pmatrix} | |
D+D^3 & 1+D^3 | D+D^3 & 1+D^3 | ||
\end{pmatrix} \cdot \begin{pmatrix} | \end{pmatrix} \cdot \begin{pmatrix} | ||
| Zeile 430: | Zeile 433: | ||
Damit ergeben sich in den drei Strängen folgende Codesquenzen: | Damit ergeben sich in den drei Strängen folgende Codesquenzen: | ||
| − | :<math>{X}^{(1)}(D) | + | ::<math>{X}^{(1)}(D) = (D + D^3) \cdot (1+D) + (1 + D^3) \cdot D =D + D^2 + D^3 + D^4 + D + D^4 = D^2 + D^3</math> |
| − | |||
| − | :<math>\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},</math> | + | :::<math>\Rightarrow \hspace{0.3cm} \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm},</math> |
| − | :<math>{X}^{(2)}(D) | + | ::<math>{X}^{(2)}(D)= (D + D^3) \cdot D + (1 + D^3) \cdot 1 = D^2 + D^4 + 1 + D^3 = 1+D^2 + D^3 + D^4</math> |
| − | |||
| − | :<math>\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm},</math> | + | :::<math>\Rightarrow \hspace{0.3cm}\underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm},</math> |
| − | :<math>{X}^{(3)}(D) | + | ::<math>{X}^{(3)}(D)=(D + D^3) \cdot (1 + D) + (1 + D^3) \cdot 1 = D + D^2 + D^3+ D^4 + 1 + D^3 = 1+ D + D^2 + D^4</math> |
| − | |||
| − | :<math>\Rightarrow \underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.</math> | + | :::<math>\Rightarrow \hspace{0.3cm}\underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm}.</math> |
Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten: | Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten: | ||
| − | * im | + | * im [[Kanalcodierung/Grundlagen_der_Faltungscodierung#Faltungscodierer_mit_zwei_Eing.C3.A4ngen|$\text{Beispiel 4}$]] des Kapitels „Grundlagen der Faltungscodierung”,<br> |
| − | *im | + | *im [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Generatormatrix_eines_Faltungscodierers_mit_Ged.C3.A4chtnis_m| $\text{Beispiel 2}$]] des aktuellen Kapitels.}}<br> |
| − | == Systematische Faltungscodes | + | == Systematische Faltungscodes == |
<br> | <br> | ||
| − | Die Polynomrepräsentation anhand der Übertragungsfunktionsmtrix | + | Die Polynomrepräsentation anhand der Übertragungsfunktionsmtrix $\mathbf{G}(D)$ ermöglicht Einblicke in die Struktur eines Faltungscodes. |
| + | |||
| + | *Beispielsweise erkennt man anhand dieser $k × n$–Matrix, ob es sich um einen [[Kanalcodierung/Allgemeine_Beschreibung_linearer_Blockcodes#Systematische_Codes| systematischen Code]] handelt. | ||
| + | *Darunter versteht man einen Code, bei dem die Codesequenzen $\underline{x}^{(1)}, \ \text{...} \ , \ \underline{x}^{(k)}$ mit den Informationssequenzen $\underline{u}^{(1)}, \ \text{...} \ , \ \underline{u}^{(k)}$ identisch sind. | ||
| − | + | *Die Grafik zeigt beispielhaft einen systematischen $(n = 4, \ k = 3)$–Faltungscode.<br> | |
| − | |||
| − | :<math>{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_{\rm sys}(D) = \ | + | [[Datei:P ID2611 KC T 3 2 S7 v2.png|center|frame|Systematischer Faltungscode mit $k = 3, \ n = 4$|class=fit]] |
| + | |||
| + | Ein systematischer $(n, k)$–Faltungscode liegt immer dann vor, wenn die Übertragungsfunktionsmatrix (mit $k$ Zeilen und $n$ Spalten) folgendes Aussehen hat: | ||
| + | |||
| + | ::<math>{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_{\rm sys}(D) = \left [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\right ] | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
Hierbei ist folgende Nomenklatur verwendet: | Hierbei ist folgende Nomenklatur verwendet: | ||
| − | * | + | *$\mathbf{I}_k$ bezeichnet eine diagonale Einheitsmatrix der Dimension $k × k$.<br> |
| − | * | + | *$\mathbf{P}(D)$ ist eine $k × (n -k)$–Matrix, wobei jedes Matrixelement ein Polynom in $D$ beschreibt.<br><br> |
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 7:}$ Ein systematischer Faltungscode mit $n = 3, \ k = 2, \ m = 2$ könnte beispielsweise die folgende Übertragungsfunktionsmatrix aufweisen: | ||
| − | :<math>{\boldsymbol{\rm G}}_{\rm sys}(D) = \begin{pmatrix} | + | ::<math>{\boldsymbol{\rm G} }_{\rm sys}(D) = \begin{pmatrix} |
1 & 0 & 1+D^2\\ | 1 & 0 & 1+D^2\\ | ||
0 & 1 & 1+D | 0 & 1 & 1+D | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Andere systematische Faltungscodes mit gleichem | + | Andere systematische Faltungscodes mit gleichem $n$ und gleichem $k$ unterscheiden sich demgegenüber nur durch die beiden Matrixelemente in der letzten Spalte.}}<br> |
| − | |||
| − | + | == Äquivalenter systematischer Faltungscode == | |
| + | <br> | ||
| + | Zu jedem $(n, \ k)$–Faltungscode mit Matrix $\mathbf{G}(D)$ gibt es einen ''äquivalenten systematischen Code'', dessen $D$–Matrix wir mit $\mathbf{G}_{\rm sys}(D)$ benennen.<br> | ||
| − | + | [[Datei:P ID2622 KC T 3 2 S7 v1.png|center|frame|Unterteilung von $\mathbf{G}(D)$ in $\mathbf{T}(D)$ und $\mathbf{Q}(D)$|class=fit]] | |
| − | + | Um von der Übertragungsfunktionsmatrix $\mathbf{G}(D)$ zur Matrix $\mathbf{G}_{\rm sys}(D)$ des äquivalenten systematischen Faltungscodes zu kommen, geht man gemäß Grafik wie folgt vor: | |
| − | + | *Man unterteilt die $k × n$–Matrix $\mathbf{G}(D)$ in eine quadratische Matrix $\mathbf{T}(D)$ mit $k$ Zeilen und $k$ Spalten und bezeichnet den Rest mit $\mathbf{Q}(D)$. | |
| − | Um von | ||
| − | *Man unterteilt die | ||
| − | *Anschließend berechnet man die zu | + | *Anschließend berechnet man die zu $\mathbf{T}(D)$ inverse Matrix $\mathbf{T}^{-1}(D)$ und daraus die Matrix für den äquivanten systematischen Code: |
::<math>{\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.</math> | ::<math>{\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.</math> | ||
| − | *Da | + | *Da $\mathbf{T}^{-1}(D) \cdot \mathbf{T}(D)$ die $k × k$–Einheitsmatrix $\mathbf{I}_k$ ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden: |
::<math>{\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] | ::<math>{\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] | ||
| Zeile 496: | Zeile 502: | ||
\hspace{0.05cm}</math> | \hspace{0.05cm}</math> | ||
| − | + | [[Datei:P ID2613 KC T 3 2 S1 neu.png|right|frame|Faltungscodierer der Rate $2/3$]] | |
| − | [[Datei:P ID2613 KC T 3 2 S1 neu.png| | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 8:}$ | |
| + | Der auf den letzten Seiten schon häufiger betrachtete Coder der Rate $2/3$ ist nicht systematisch, weil zum Beispiel $\underline{x}^{(1)} ≠ \underline{u}^{(1)}, \ \underline{x}^{(2)} ≠ \underline{u}^{(2)}$ gilt (siehe nebenstehende Coderschaltung).<br> | ||
Man erkennt dies aber auch anhand der Übertragungsfunktionsmatrix: | Man erkennt dies aber auch anhand der Übertragungsfunktionsmatrix: | ||
| − | :<math>{\boldsymbol{\rm G}}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm T}}(D)\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}\big ]</math> | + | ::<math>{\boldsymbol{\rm G} }(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm T} }(D)\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm Q} }(D) \hspace{0.05cm}\big ]</math> |
| − | :<math>\Rightarrow \hspace{0.3cm} | + | ::<math>\Rightarrow \hspace{0.3cm} |
| − | {\boldsymbol{\rm T}}(D) = \begin{pmatrix} | + | {\boldsymbol{\rm T} }(D) = \begin{pmatrix} |
1+D & D\\ | 1+D & D\\ | ||
D & 1 | D & 1 | ||
\end{pmatrix}\hspace{0.05cm},\hspace{0.2cm} | \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm} | ||
| − | {\boldsymbol{\rm Q}}(D) = \begin{pmatrix} | + | {\boldsymbol{\rm Q} }(D) = \begin{pmatrix} |
1+D \\ | 1+D \\ | ||
1 | 1 | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Die Determinante von | + | Die Determinante von $\mathbf{T}(D)$ ergibt sich zu $(1 + D) \cdot 1 + D \cdot D = 1 + D + D^2$ und ist ungleich Null. |
| + | |||
| + | Somit kann für die Inverse von $\mathbf{T}(D)$ geschrieben werden (Vertauschung der Diagonalelemente!): | ||
| − | :<math>{\boldsymbol{\rm T}}^{-1}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} | + | ::<math>{\boldsymbol{\rm T} }^{-1}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} |
1 & D\\ | 1 & D\\ | ||
D & 1+D | D & 1+D | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | Das Produkt | + | Das Produkt $\mathbf{T}(D) \cdot \mathbf{T}^{–1}(D)$ ergibt die Einheitsmatrix $\mathbf{I}_2$, und für die dritte Spalte von $\mathbf{G}_{\rm sys}(D)$ gilt: |
| − | :<math>{\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) | + | ::<math>{\boldsymbol{\rm P} }(D)= {\boldsymbol{\rm T} }^{-1}(D) \cdot {\boldsymbol{\rm Q} }(D) |
= \frac{1}{1+D+D^2} \cdot \begin{pmatrix} | = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} | ||
1 & D\\ | 1 & D\\ | ||
| Zeile 532: | Zeile 541: | ||
\end{pmatrix} </math> | \end{pmatrix} </math> | ||
| − | :<math>\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm P}}(D) | + | ::<math>\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm P} }(D) |
= \frac{1}{1+D+D^2} \cdot \begin{pmatrix} | = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} | ||
(1+D) + D \\ | (1+D) + D \\ | ||
| Zeile 542: | Zeile 551: | ||
\end{pmatrix} </math> | \end{pmatrix} </math> | ||
| − | :<math>\Rightarrow \hspace{0.2cm}{\boldsymbol{\rm G}}_{\rm sys}(D) = | + | ::<math>\Rightarrow \hspace{0.2cm}{\boldsymbol{\rm G} }_{\rm sys}(D) = |
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 0 & \frac{1}{1+D+D^2}\\ | 1 & 0 & \frac{1}{1+D+D^2}\\ | ||
| Zeile 548: | Zeile 557: | ||
\end{pmatrix}\hspace{0.05cm}. </math> | \end{pmatrix}\hspace{0.05cm}. </math> | ||
| − | + | Zu klären ist noch, wie das Filter einer solchen gebrochen–rationalen Übertragungsfunktion aussieht.}}<br> | |
== Filterstruktur bei gebrochen–rationaler Übertragungsfunktion == | == Filterstruktur bei gebrochen–rationaler Übertragungsfunktion == | ||
<br> | <br> | ||
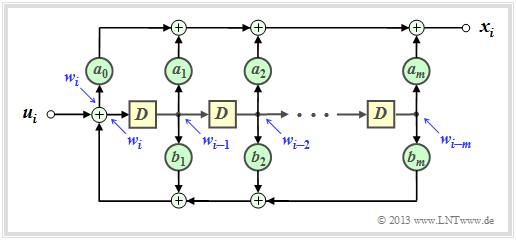
| − | + | [[Datei:P ID2619 KC T 3 2 S8 v1.png|right|frame|Rekursives Filter zur Realisierung von $G(D) = A(D)/B(D)$|class=fit]] | |
| − | + | Hat eine Übertragungsfunktion die Form $G(D) = A(D)/B(D)$, so bezeichnet man das zugehörige Filter als <i>rekursiv</i>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Datei:P ID2619 KC T 3 2 S8 v1.png|Rekursives Filter zur Realisierung von | ||
| − | |||
| − | |||
| − | {{ | + | Bei einem rekursiven Faltungscodierer mit dem Gedächtnis $m$ kann für die beiden Polynome $A(D)$ und $B(D)$ allgemein geschrieben werden: |
| + | ::<math>A(D) = \sum_{l = 0}^{m} a_l \cdot D\hspace{0.05cm}^l = a_0 + a_1 \cdot D + a_2 \cdot D^2 +\ \text{...} \ \hspace{0.05cm} + a_m \cdot D\hspace{0.05cm}^m \hspace{0.05cm},</math> | ||
| + | ::<math>B(D) = 1 + \sum_{l = 1}^{m} b_l \cdot D\hspace{0.05cm}^l = 1 + b_1 \cdot D + b_2 \cdot D^2 + \ \text{...} \ \hspace{0.05cm} + b_m \cdot D\hspace{0.05cm}^m \hspace{0.05cm}.</math> | ||
| − | :< | + | Die Grafik zeigt die entsprechende Filterstruktur in der so genannten <i>Controller Canonical Form</i>:<br> |
| − | : | + | *Die Koeffizienten $a_0, \ \text{...} \ , \ a_m$ beschreiben den Vorwärtszweig. |
| + | * Die Koeffizienten $b_1, \ \text{...} \ , \ b_m$ bilden eine Rückkopplung. | ||
| + | *Alle Koeffizienten sind binär, also $1$ (durchgehende Verbindung) oder $0$ (fehlende Verbindung). | ||
| + | <br clear=all> | ||
| + | [[Datei:P_ID2620__KC_T_3_2_S8b_neu.png|right|frame|Filter: $G(D) = (1+D^2)/(1+D +D^2)$|class=fit]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 9:}$ Die rechts skizzierte Filterstruktur lässt sich wie folgt beschreiben: | ||
| − | + | ::<math>x_i = w_i + w_{i-2} \hspace{0.05cm},</math> | |
| + | ::<math>w_i = u_i + w_{i-1}+ w_{i-2} \hspace{0.05cm}.</math> | ||
| − | + | Entsprechend gilt für die $D$–Transformierten: | |
| − | : | ||
| − | :<math>W(D) = \hspace{0.08cm} U(D) + W(D) \cdot D+ W(D) \cdot D^2 | + | ::<math>X(D) =W(D) + W(D) \cdot D^2 =W(D) \cdot \left ( 1+ D^2 \right ) \hspace{0.05cm},</math> |
| + | ::<math>W(D) = \hspace{0.08cm} U(D) + W(D) \cdot D+ W(D) \cdot D^2</math> | ||
| + | ::<math>\Rightarrow \hspace{0.3cm} | ||
U(D) = W(D) \cdot \left ( 1+ D + D^2 \right ) \hspace{0.05cm}.</math> | U(D) = W(D) \cdot \left ( 1+ D + D^2 \right ) \hspace{0.05cm}.</math> | ||
Somit erhält man für die Übertragungsfunktion dieses Filters: | Somit erhält man für die Übertragungsfunktion dieses Filters: | ||
| − | :<math>G(D) = \frac{X(D)}{U(D)} = \frac{1+D^2}{1+D+D^2} \hspace{0.05cm}. </math> | + | ::<math>G(D) = \frac{X(D)}{U(D)} = \frac{1+D^2}{1+D+D^2} \hspace{0.05cm}. </math> |
| − | Im [ | + | Im [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#.C3.84quivalenter_systematischer_Faltungscode| $\text{Beispiel 8}$]] zum äquivalenten systematischen Faltungscode hat sich im unteren Zweig genau dieser Ausdruck ergeben.}}<br> |
| − | == Aufgaben == | + | == Aufgaben zum Kapitel== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.2:_G–Matrix_eines_Faltungscodierers|Aufgabe 3.2: G–Matrix eines Faltungscodierers]] |
| − | [[ | + | [[Aufgaben:Aufgabe_3.2Z:_(3,_1,_3)–Faltungscodierer|Aufgabe 3.2Z: (3, 1, 3)–Faltungscodierer]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.3:_Codesequenzberechnung_über_U(D)_und_G(D)|Aufgabe 3.3: Codesequenzberechnung über U(D) und G(D)]] |
| − | [[ | + | [[Aufgaben:Aufgabe_3.3Z:_Faltung_und_D–Transformation|Aufgabe 3.3Z: Faltung und D–Transformation]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.4:_Systematische_Faltungscodes|Aufgabe 3.4: Systematische Faltungscodes]] |
| − | [[ | + | [[Aufgaben:Aufgabe_3.4Z:_Äquivalente_Faltungscodes|Aufgabe 3.4Z: Äquivalente Faltungscodes?]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.5:_Rekursive_Filter_für_GF(2)|Aufgabe 3.5: Rekursive Filter für GF(2)]] |
{{Display}} | {{Display}} | ||
Aktuelle Version vom 4. Juni 2019, 15:44 Uhr
Inhaltsverzeichnis
- 1 Aufteilung der Generatormatrix in Teilmatrizen
- 2 Generatormatrix eines Faltungscodierers mit Gedächtnis m
- 3 Generatormatrix für Faltungscodierer der Rate 1/n
- 4 GF(2)–Beschreibungsformen eines Digitalen Filters
- 5 Anwendung der D–Transformation auf Rate–1/n–Faltungscoder
- 6 Übertragungsfunktionsmatrix – Transfer Function Matrix
- 7 Systematische Faltungscodes
- 8 Äquivalenter systematischer Faltungscode
- 9 Filterstruktur bei gebrochen–rationaler Übertragungsfunktion
- 10 Aufgaben zum Kapitel
Aufteilung der Generatormatrix in Teilmatrizen
Entsprechend den Ausführungen im früheren Abschnitt Lineare Codes und zyklische Codes lässt sich das Codewort $\underline{x}$ eines linearen Blockcodes aus dem Informationswort $\underline{u}$ und der Generatormatrix $\mathbf{G}$ in einfacher Weise ermitteln: $\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}}$. Dabei gilt:
- Die Vektoren $\underline{u}$ und $\underline{x}$ haben die Länge $k$ (Bitanzahl eines Informationswortes) bzw. $n$ (Bitanzahl eines Codewortes) und $\mathbf{G}$ besitzt die Dimension $k × n$ $(k$ Zeilen und $n$ Spalten$)$.
- Bei Faltungscodierung bezeichnen dagegen $\underline{u}$ und $\underline{x}$ Sequenzen mit $k\hspace{0.05cm}' → ∞$ und $n\hspace{0.05cm}' → ∞$. Deshalb wird auch die Generatormatrix $\mathbf{G}$ in beiden Richtungen unendlich weit ausgedehnt sein.
Als Vorbereitung für die Einführung der Generatormatrix $\mathbf{G}$ auf der nächsten Seite definieren wir $m + 1$ Teilmatrizen, jeweils mit $k$ Zeilen und $n$ Spalten, die wir mit $\mathbf{G}_l$ bezeichnen, wobei $0 ≤ l ≤ m$ gilt.
$\text{Definition:}$ Die Teilmatrix $\mathbf{G}_l$ beschreibt folgenden Sachverhalt: Ist das Matrixelement $\mathbf{G}_l(\kappa, j) = 1$, so sagt dies aus, dass das Codebit $x_i^{(j)}$ durch das Informationsbit $u_{i-l}^{(\kappa)}$ beeinflusst wird. Andernfalls ist dieses Matrixelement gleich $0$.
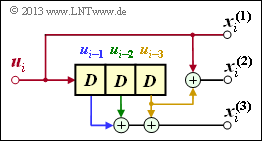
Diese Definition wird nun an einem Beispiel verdeutlicht.
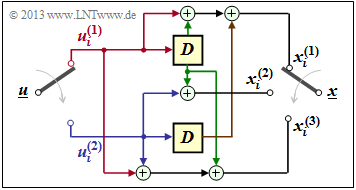
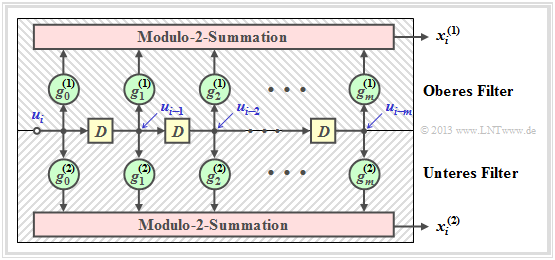
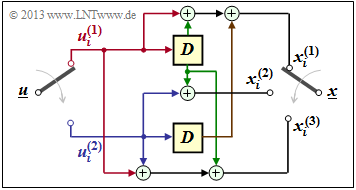
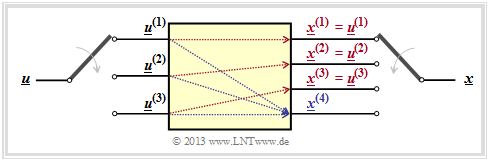
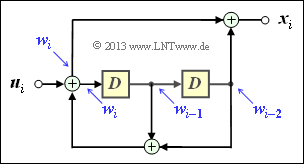
$\text{Beispiel 1:}$ Wir betrachten wiederum den Faltungscodierer gemäß der Grafik mit folgenden Codebits:
- \[x_i^{(1)} = u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\]
- \[x_i^{(2)} = u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\]
- \[x_i^{(3)} = u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]
Wegen der Gedächtnisordnung $m = 1$ wird dieser Codierer durch die beiden Teilmatrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ vollständig charakterisiert:
- \[{ \boldsymbol{\rm G} }_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G} }_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]
Diese Matrizen sind wie folgt zu interpretieren:
- Erste Zeile von $\mathbf{G}_0$, rote Pfeile: $\hspace{1.1cm}u_i^{(1)}$ beeinflusst sowohl $x_i^{(1)}$ als auch $x_i^{(3)}$, nicht jedoch $x_i^{(2)}$.
- Zweite Zeile von $\mathbf{G}_0$, blaue Pfeile: $\hspace{0.6cm}u_i^{(2)}$ beeinflusst $x_i^{(2)}$ und $x_i^{(3)}$, aber nicht $x_i^{(1)}$.
- Erste Zeile von $\mathbf{G}_1$, grüne Pfeile: $\hspace{0.9cm}u_{i-1}^{(1)}$ beeinflusst alle drei Coderausgänge.
- Zweite Zeile von $\mathbf{G}_1$, brauner Pfeil: $\hspace{0.45cm}u_{i-1}^{(2)}$ beeinflusst nur $x_i^{(1)}$.
Generatormatrix eines Faltungscodierers mit Gedächtnis m
Mit den Teilmatrizen $\mathbf{G}_0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \mathbf{G}_m$ lassen sich die $n$ Codebits zum Zeitpunkt $i$ wie folgt ausdrücken:
- \[\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 +\hspace{0.05cm} \text{...} \hspace{0.05cm} + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m \hspace{0.05cm}.\]
Hierbei sind folgende vektorielle Größen zu berücksichtigen:
- \[\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.\]
Betrachtet man die bei $i = 1$ beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen
- \[\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}\text{...} \hspace{0.1cm} \big)\hspace{0.05cm},\]
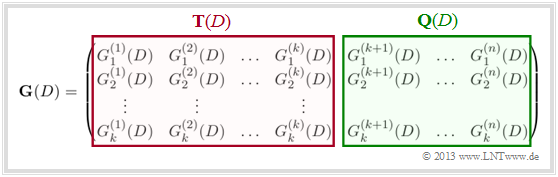
so kann dieser Zusammenhang durch die Matrixgleichung $\underline{x} = \underline{u} \cdot \mathbf{G}$ ausgedrückt werden. Hierbei ist für die Generatormatrix $\mathbf{G}$ wie folgt zu setzen:
- \[{ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \cdots & \cdots & & & \cdots \end{pmatrix}\hspace{0.05cm}.\]
- Aus der Gleichung erkennt man sofort das Gedächtnis $m$ des Faltungscodes. Die Parameter $k$ und $n$ sind direkt nicht ablesbar.
- Sie sind aber durch die Zeilen– und Spaltenanzahl der Teilmatrizen $\mathbf{G}_l$ festgelegt.
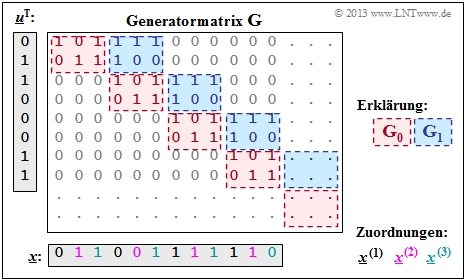
$\text{Beispiel 2:}$ Mit den zwei Matrizen $\mathbf{G}_0$ und $\mathbf{G}_1$ – siehe $\text{Beispiel 1}$ – erhält man die rechts skizzierte Matrix $\mathbf{G}$.
Anzumerken ist:
- Die Generatormatrix $\mathbf{G}$ erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur acht Zeilen und zwölf Spalten.
- Für die zeitlich begrenzte Informationssequenz $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1)$ ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann:
- $$\underline{x} = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0).$$
- Anhand der Beschriftungsfarben lassen sich die $n = 3$ Codewortstränge ablesen.
- Das gleiche Ergebnis haben wir (auf anderem Wege) im $\text{Beispiel 4}$ am Ende des letzten Kapitels erhalten:
- $$\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.$$
Generatormatrix für Faltungscodierer der Rate 1/n
Wir betrachten nun den Sonderfall $k = 1$,
- zum einen aus Gründen einer möglichst einfachen Darstellung,
- aber auch, weil Faltungscodierer der Rate $1/n$ für die Praxis eine große Bedeutung besitzen.
Faltungscodierer mit $k = 1, \ n = 2, \ m = 1$
Aus nebenstehender Skizze kann abgeleitet werden:
- \[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 1 \end{pmatrix}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 01 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 01 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 01 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 01 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Für die Eingangssequenz $\underline{u} = (1, 0, 1, 1)$ beginnt die Codesequenz mit $\underline{x} = (1, 1, 0, 1, 1, 1, 1, 0, \ \text{...})$.
Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Generatormatrix.
Faltungscodierer mit $k = 1, \ n = 2, \ m = 2$
Aufgrund der Gedächtnisordnung $m = 2$ gibt es hier drei Teilmatrizen:
- \[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 1 & 1 \end{pmatrix}\]
Damit lautet die resultierende Generatormatrix:
- \[ { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]
Hier führt die Eingangsssequenz $\underline{u} = (1, 0, 1, 1)$ zur Codesequenz $\underline{x} = (1, 1, 1, 0, 0, 0, 0, 1, \ \text{...})$.
Faltungscodierer mit $k = 1, \ n = 3, \ m = 3$
Wegen $m = 3$ gibt es nun vier Teilmatrizen der jeweiligen Dimension $1 × 3$:
- \[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_3=\begin{pmatrix} 0 & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]
Damit lautet die resultierende Generatormatrix:
- \[{ \boldsymbol{\rm G}}=\begin{pmatrix} 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm},\]
und man erhält für $\underline{u} = (1, 0, 1, 1)$ die Codesequenz $\underline{x} = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, \ \text{...})$.
GF(2)–Beschreibungsformen eines Digitalen Filters
Im Kapitel Grundlagen der Faltungscodierung wurde bereits darauf hingewiesen,
- dass ein Rate $1/n$–Faltungscodierer durch mehrere Digitale Filter realisiert werden kann,
- wobei die Filter parallel mit der gleichen Eingangsfolge $\underline{u}$ arbeiten.
Bevor wir diese Aussage vertiefen, sollen zuerst die Eigenschaften eines Digitalfilters für das Galoisfeld ${\rm GF(2)}$ genannt werden.
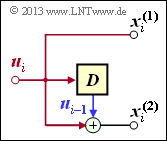
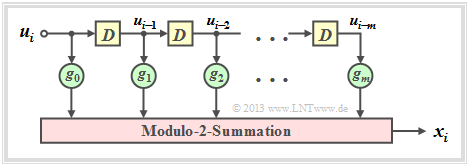
Die Grafik ist wie folgt zu interpretieren:
- Das Filter besitzt die Impulsantwort $\underline{g} = (g_0, g_1, g_2, \ \text{...} \ , g_m)$.
- Für alle Filterkoeffizienten $($mit den Indizes $0 ≤ l ≤ m)$ gilt: $g_l ∈ {\rm GF}(2) = \{0, 1\}$.
- Die einzelnen Symbole $u_i$ der Eingangsfolge $\underline{u}$ seien ebenfalls binär: $u_i ∈ \{0, 1\}$.
- Damit gilt für das Ausgangssymbol zu den Zeitpunkten $i ≥ 1$ mit Addition und Multiplikation in ${\rm GF(2)}$:
- \[x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.\]
- Dies entspricht der (zeitdiskreten) Faltungsoperation (englisch: Convolution ), gekennzeichnet durch einen Stern. Damit kann für die gesamte Ausgangssequenz geschrieben werden:
- \[\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.\]
- Wesentlicher Unterschied gegenüber dem Kapitel Digitale Filter im Buch „Stochastische Signaltheorie” ist die Modulo–2–Addition $(1 + 1 = 0)$ anstelle der herkömmlichen Addition $(1 + 1 = 2)$.
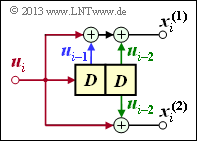
$\text{Beispiel 3:}$ Die Impulsantwort des dargestellten Digitalen Filters dritter Ordnung lautet: $\underline{g} = (1, 0, 1, 1)$.
- Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt: $\underline{u} = (1, 1, 0, 0, 0, \ \text{ ...})$.
- Damit ergibt sich die (unendliche) Ausgangssequenz $\underline{x}$ im binären Galoisfeld ⇒ ${\rm GF(2)}$:
- \[\underline{x} = (\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1\hspace{0.05cm})\]
- \[\Rightarrow \hspace{0.3cm} \underline{x} =(\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}0,\hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} \hspace{0.05cm} \text{ ...}\hspace{0.05cm}) = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.\]
- Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet:
- \[\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.\]
Zeitdiskrete Signale kann man aber auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.
$\text{Definition:}$ Die zum zeitdiskreten Signal $\underline{x} = (x_0, x_1, x_2, \ \text{...})$ gehörige $D$–Transformierte lautet:
- \[X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}\text{...}\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.\]
Für diese spezielle Transformation in einen Bildbereich verwenden wir auch folgende Notation, wobei „$D$” für Delay Operator steht:
- \[\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.\]
Hinweis: In der Literatur wird manchmal $x(D)$ anstelle von $X(D)$ verwendet. Wir schreiben in unserem Lerntutorial aber alle Bildbereichsfunktionen mit Großbuchstaben, zum Beispiel die Fourier–, die Laplace– und die $D$–Transformation:
- \[x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\hspace{0.15cm} X(p) \hspace{0.05cm},\hspace{0.4cm} \underline{x} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} X(D) \hspace{0.05cm}.\]
Wir wenden nun die $D$–Transformation auch auf die Informationssequenz $\underline{u}$ und die Impulsantwort $\underline{g}$ an. Aufgrund der zeitlichen Begrenzung von $\underline{g}$ ergibt sich die obere Summationsgrenze bei $G(D)$ zu $i = m$:
- \[\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}\text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = \sum_{i = 0}^{\infty} u_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm},\]
- \[\underline{g} = (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, g_m) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = \sum_{i = 0}^{m} g_i \cdot D\hspace{0.05cm}^i \hspace{0.05cm}.\]
$\text{Satz:}$ Wie bei allen Spektraltransformationen gilt auch bei der $D$–Transformation im Bildbereich die Multiplikation, da die (diskreten) Zeitsignale $\underline{u}$ und $\underline{g}$ durch die Faltung verknüpft sind:
- \[\underline{x} = \underline{u} * \underline{g} \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = U(D) \cdot G(D) \hspace{0.05cm}.\]
Man bezeichnet – wie in der Systemtheorie allgemein üblich – auch die $D$–Transformierte $G(D)$ der Impulsantwort $\underline{g}$ als Übertragungsfunktion (englisch: Transfer Function). Der (recht einfache) $\rm Beweis$ dieses wichtigen Ergebnisses finden Sie in der Angabe zur Aufgabe 3.3Z.
$\text{Beispiel 4:}$ Wir betrachten wieder die zeitdiskreten Signale
- \[\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D \hspace{0.05cm},\]
- \[\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.\]
Wie im $\text{Beispiel 3}$ (auf dieser Seite oben) erhält man auch auf diesem Lösungsweg:
- \[X(D) = U(D) \cdot G(D) = (1+D) \cdot (1+ D^2 + D^3) \]
- \[\Rightarrow \hspace{0.3cm} X(D) = 1+ D^2 + D^3 +D + D^3 + D^4 = 1+ D + D^2 + D^4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \text{...} \hspace{0.05cm}) \hspace{0.05cm}.\]
Die Multiplikation mit $D$ im Bildbereich entspricht im Zeitbereich einer Verschiebung um eine Stelle nach rechts, weshalb man $D$ als Verzögerungsoperator (englisch: Delay Operator ) bezeichnet:
- \[W(D) = D \cdot X(D) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \text{...} \hspace{0.05cm}) \hspace{0.05cm}.\]
Anwendung der D–Transformation auf Rate–1/n–Faltungscoder
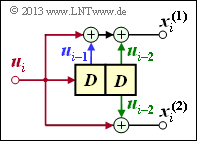
Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall $k = 1$ beschränken.
- Ein solcher $(n, \ k = 1)$–Faltungscode lässt sich mit $n$ Digitalen Filtern realisieren, die auf der gleichen Informationssequenz $\underline{u}$ parallel arbeiten.
- Die Grafik zeigt die Anordnung für den Codeparameter $n = 2$ ⇒ Coderate $R = 1/2$.
Die folgenden Gleichungen gelten für beide Filter gleichermaßen, wobei für das obere Filter $j = 1$ und für das untere Filter $j = 2$ zu setzen ist:
- Die Impulsantworten der beiden Filter ergeben sich zu
- \[\underline{g}^{(j)} = (g_0^{(j)}, g_1^{(j)}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, g_m^{(j)}\hspace{0.01cm}) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
- Die zwei Ausgangssequenzen lauten, wobei berücksichtigt ist, dass beide Filter auf der gleichen Eingangssequenz $\underline{u} = (u_0, u_1, u_2, \hspace{0.05cm} \text{...})$ arbeiten:
- \[\underline{x}^{(j)} = (x_0^{(j)}, x_1^{(j)}, x_2^{(j)}, \hspace{0.05cm}\text{...}\hspace{0.05cm}) = \underline{u} \cdot \underline{g}^{(j)} \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
- Für die $D$–Transformierten der Ausgangssequenzen gilt:
- \[X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]
Um diesen Sachverhalt kompakter darstellen zu können, definieren wir nun folgende vektorielle Größen eines Faltungscodes der Rate $1/n$:
$\text{Definition:}$ Die $D$–Übertragungsfunktionen der $n$ parallel angeordneten Digitalen Filter werden im Vektor $\underline{G}(D)$ zusammengefasst:
- \[\underline{G}(D) = \left ( G^{(1)}(D), G^{(2)}(D), \hspace{0.05cm}\text{...}\hspace{0.1cm}, G^{(n)} (D) \right )\hspace{0.05cm}.\]
- Der Vektor $\underline{X}(D)$ beinhaltet die $D$–Transformierten der $n$ Codesequenzen $\underline{x}^{(1)}, \underline{x}^{(2)}, \ \text{...} \ , \underline{x}^{(n)}$:
- \[\underline{X}(D) = \left ( X^{(1)}(D), X^{(2)}(D), \hspace{0.05cm}\text{...}\hspace{0.1cm}, X^{(n)} (D) \right )\hspace{0.05cm}.\]
- Damit erhält man die folgende Vektorgleichung:
- \[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]
- Aufgrund des Codeparameters $k = 1$ ist $U(D)$ hier keine vektorielle Größe.
$\text{Beispiel 5:}$ Wir betrachten den Faltungscodierer mit den Codeparametern $n = 2, \ k = 1, \ m = 2$. Für diesen gilt:
- \[\underline{g}^{(1)} =(\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D + D^2 \hspace{0.05cm},\]
- \[\underline{g}^{(2)}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 \]
- \[\Rightarrow \hspace{0.3cm} \underline{G}(D) = \big ( 1+ D + D^2 \hspace{0.05cm}, \hspace{0.1cm}1+ D^2 \big )\hspace{0.05cm}.\]
Die Informationssequenz sei $\underline{u} = (1, 0, 1, 1)$ ⇒ $D$–Transformierte $U(D) = 1 + D^2 + D^3$. Damit erhält man:
- \[\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}\]
wobei
- \[{X}^{(1)}(D) = (1+ D^2 + D^3) \cdot (1+ D + D^2)=1+ D + D^2 + D^2 + D^3 + D^4 + D^3 + D^4 + D^5 = 1+ D + D^5\]
- \[\Rightarrow \hspace{0.3cm} \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},\]
- \[{X}^{(2)}(D) = (1+ D^2 + D^3) \cdot (1+ D^2)=1+ D^2 + D^2 + D^4 + D^3 + D^5 = 1+ D^3 + D^4 + D^5\]
- \[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.\]
Das gleiche Ergebnis haben wir in der Aufgabe 3.1Z auf anderem Wege erhalten. Nach dem Multplexen der beiden Stränge erhält man wieder:
- $$\underline{x} = (11, 10, 00, 01, 01, 11, 00, 00, \hspace{0.05cm} \text{...} \hspace{0.05cm}).$$
Übertragungsfunktionsmatrix – Transfer Function Matrix
Wir haben gesehen, dass ein Faltungscode der Rate $1/n$ sich am kompaktesten als Vektorgleichung im $D$–transformierten Bereich beschreiben lässt: $\underline{X}(D) = U(D) \cdot \underline{G}(D)$.
Nun erweitern wir das Resultat auf Faltungscodierer mit mehr als einem Eingang ⇒ $k ≥ 2$ (siehe Grafik).
Um einen Faltungscode der Rate $k/n$ im $D$–Bereich abbilden zu können, muss die Dimension obiger Vektorgleichung hinsichtlich Eingang und Übertragungsfunktion erhöht werden:
- \[\underline{X}(D) = \underline{U}(D) \cdot { \boldsymbol{\rm G}}(D)\hspace{0.05cm}.\]
Dazu sind folgende Maßnahmen erforderlich:
- Aus der skalaren Funktion $U(D)$ wird der Vektor $\underline{U}(D) = (U^{(1)}(D), \ U^{(2)}(D), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ U^{(k)}(D))$.
- Aus dem Vektor $\underline{G}(D)$ wird die $k × n$–Übertragungsfunktionsmatrix $\mathbf{G}(D)$ (englisch: Transfer Function Matrix oder Polynomial Generator Matrix):
- \[{\boldsymbol{\rm G}}(D)=\begin{pmatrix} G_1^{(1)}(D) & G_1^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_1^{(n)}(D)\\ G_2^{(1)}(D) & G_2^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_2^{(n)}(D)\\ \vdots & \vdots & & \vdots\\ G_k^{(1)}(D) & G_k^{(2)}(D) & \hspace{0.05cm} \text{...} \hspace{0.05cm} & G_k^{(n)}(D) \end{pmatrix}\hspace{0.05cm}.\]
- Jedes der $k \cdot n$ Matrixelemente $G_i^{(j)}(D)$ mit $1 ≤ i ≤ k,\ \ 1 ≤ j ≤ n$ ist ein Polynom über der Dummy–Variablen $D$ im Galoisfeld ${\rm GF}(2)$, maximal vom Grad $m$, wobei $m$ das Gedächtnis angibt.
- Für die obige Übertragungsfunktionsmatrix kann mit den zu Beginn dieses Kapitels definierten Teilmatrizen $\mathbf{G}_0, \ \text{...} \ , \mathbf{G}_m$ auch geschrieben werden $($als Index verwenden wir wieder $l)$:
- \[{\boldsymbol{\rm G}}(D) = \sum_{l = 0}^{m} {\boldsymbol{\rm G}}_l \cdot D\hspace{0.03cm}^l = {\boldsymbol{\rm G}}_0 + {\boldsymbol{\rm G}}_1 \cdot D + {\boldsymbol{\rm G}}_2 \cdot D^2 + \hspace{0.05cm} \text{...} \hspace{0.05cm}+ {\boldsymbol{\rm G}}_m \cdot D\hspace{0.03cm}^m \hspace{0.05cm}.\]
$\text{Beispiel 6:}$ Wir betrachten den $(n = 3, \ k = 2, \ m = 1)$–Faltungscoder, dessen Teilmatrizen bereits im $\text{Beispiel 1}$ wie folgt ermittelt wurden:
- \[{ \boldsymbol{\rm G} }_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G} }_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]
Wegen $m = 1$ existieren keine Teilmatrizen für $l ≥ 2$. Damit lautet die Übertragungsfunktionsmatrix:
- \[{\boldsymbol{\rm G} }(D) = {\boldsymbol{\rm G} }_0 + {\boldsymbol{\rm G} }_1 \cdot D = \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix} \hspace{0.05cm}.\]
Die (zeitlich begrenzte) Informationssequenz sei $\underline{u} = (0, 1, 1, 0, 0, 0, 1, 1)$, woraus sich die beiden Eingangsfolgen wie folgt ergeben:
- \[\underline{u}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(1)}(D) = D + D^3 \hspace{0.05cm},\]
- \[\underline{u}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad {U}^{(2)}(D) = 1 + D^3 \hspace{0.05cm}.\]
Daraus folgt für den Vektor der $D$–Transformierten am Coderausgang:
- \[\underline{X}(D) = \big (\hspace{0.05cm} {X}^{(1)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(2)}(D)\hspace{0.05cm}, \hspace{0.05cm} {X}^{(3)}(D)\hspace{0.05cm}\big ) = \underline{U}(D) \cdot {\boldsymbol{\rm G} }(D) \begin{pmatrix} D+D^3 & 1+D^3 \end{pmatrix} \cdot \begin{pmatrix} 1+D & D & 1+D\\ D & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]
Damit ergeben sich in den drei Strängen folgende Codesquenzen:
- \[{X}^{(1)}(D) = (D + D^3) \cdot (1+D) + (1 + D^3) \cdot D =D + D^2 + D^3 + D^4 + D + D^4 = D^2 + D^3\]
- \[\Rightarrow \hspace{0.3cm} \underline{x}^{(1)} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm},\]
- \[{X}^{(2)}(D)= (D + D^3) \cdot D + (1 + D^3) \cdot 1 = D^2 + D^4 + 1 + D^3 = 1+D^2 + D^3 + D^4\]
- \[\Rightarrow \hspace{0.3cm}\underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm},\]
- \[{X}^{(3)}(D)=(D + D^3) \cdot (1 + D) + (1 + D^3) \cdot 1 = D + D^2 + D^3+ D^4 + 1 + D^3 = 1+ D + D^2 + D^4\]
- \[\Rightarrow \hspace{0.3cm}\underline{x}^{(3)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm}.\]
Die gleichen Ergebnisse haben wir auf anderen Wegen bereits in vorherigen Beispielen erhalten:
- im $\text{Beispiel 4}$ des Kapitels „Grundlagen der Faltungscodierung”,
- im $\text{Beispiel 2}$ des aktuellen Kapitels.
Systematische Faltungscodes
Die Polynomrepräsentation anhand der Übertragungsfunktionsmtrix $\mathbf{G}(D)$ ermöglicht Einblicke in die Struktur eines Faltungscodes.
- Beispielsweise erkennt man anhand dieser $k × n$–Matrix, ob es sich um einen systematischen Code handelt.
- Darunter versteht man einen Code, bei dem die Codesequenzen $\underline{x}^{(1)}, \ \text{...} \ , \ \underline{x}^{(k)}$ mit den Informationssequenzen $\underline{u}^{(1)}, \ \text{...} \ , \ \underline{u}^{(k)}$ identisch sind.
- Die Grafik zeigt beispielhaft einen systematischen $(n = 4, \ k = 3)$–Faltungscode.
Ein systematischer $(n, k)$–Faltungscode liegt immer dann vor, wenn die Übertragungsfunktionsmatrix (mit $k$ Zeilen und $n$ Spalten) folgendes Aussehen hat:
- \[{\boldsymbol{\rm G}}(D) = {\boldsymbol{\rm G}}_{\rm sys}(D) = \left [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\right ] \hspace{0.05cm}.\]
Hierbei ist folgende Nomenklatur verwendet:
- $\mathbf{I}_k$ bezeichnet eine diagonale Einheitsmatrix der Dimension $k × k$.
- $\mathbf{P}(D)$ ist eine $k × (n -k)$–Matrix, wobei jedes Matrixelement ein Polynom in $D$ beschreibt.
$\text{Beispiel 7:}$ Ein systematischer Faltungscode mit $n = 3, \ k = 2, \ m = 2$ könnte beispielsweise die folgende Übertragungsfunktionsmatrix aufweisen:
- \[{\boldsymbol{\rm G} }_{\rm sys}(D) = \begin{pmatrix} 1 & 0 & 1+D^2\\ 0 & 1 & 1+D \end{pmatrix}\hspace{0.05cm}.\]
Andere systematische Faltungscodes mit gleichem $n$ und gleichem $k$ unterscheiden sich demgegenüber nur durch die beiden Matrixelemente in der letzten Spalte.
Äquivalenter systematischer Faltungscode
Zu jedem $(n, \ k)$–Faltungscode mit Matrix $\mathbf{G}(D)$ gibt es einen äquivalenten systematischen Code, dessen $D$–Matrix wir mit $\mathbf{G}_{\rm sys}(D)$ benennen.
Um von der Übertragungsfunktionsmatrix $\mathbf{G}(D)$ zur Matrix $\mathbf{G}_{\rm sys}(D)$ des äquivalenten systematischen Faltungscodes zu kommen, geht man gemäß Grafik wie folgt vor:
- Man unterteilt die $k × n$–Matrix $\mathbf{G}(D)$ in eine quadratische Matrix $\mathbf{T}(D)$ mit $k$ Zeilen und $k$ Spalten und bezeichnet den Rest mit $\mathbf{Q}(D)$.
- Anschließend berechnet man die zu $\mathbf{T}(D)$ inverse Matrix $\mathbf{T}^{-1}(D)$ und daraus die Matrix für den äquivanten systematischen Code:
- \[{\boldsymbol{\rm G}}_{\rm sys}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm G}}(D) \hspace{0.05cm}.\]
- Da $\mathbf{T}^{-1}(D) \cdot \mathbf{T}(D)$ die $k × k$–Einheitsmatrix $\mathbf{I}_k$ ergibt, kann die Übertragungsfunktionsmatrix des äquivalenten systematischen Codes in der gewünschten Form geschrieben werden:
- \[{\boldsymbol{\rm G}}_{\rm sys}(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm I}}_k\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm P}}(D) \hspace{0.05cm}\big ] \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\boldsymbol{\rm P}}(D)= {\boldsymbol{\rm T}}^{-1}(D) \cdot {\boldsymbol{\rm Q}}(D) \hspace{0.05cm}. \hspace{0.05cm}\]
$\text{Beispiel 8:}$
Der auf den letzten Seiten schon häufiger betrachtete Coder der Rate $2/3$ ist nicht systematisch, weil zum Beispiel $\underline{x}^{(1)} ≠ \underline{u}^{(1)}, \ \underline{x}^{(2)} ≠ \underline{u}^{(2)}$ gilt (siehe nebenstehende Coderschaltung).
Man erkennt dies aber auch anhand der Übertragungsfunktionsmatrix:
- \[{\boldsymbol{\rm G} }(D) = \big [ \hspace{0.05cm} {\boldsymbol{\rm T} }(D)\hspace{0.05cm} ; \hspace{0.1cm} {\boldsymbol{\rm Q} }(D) \hspace{0.05cm}\big ]\]
- \[\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm T} }(D) = \begin{pmatrix} 1+D & D\\ D & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm} {\boldsymbol{\rm Q} }(D) = \begin{pmatrix} 1+D \\ 1 \end{pmatrix}\hspace{0.05cm}.\]
Die Determinante von $\mathbf{T}(D)$ ergibt sich zu $(1 + D) \cdot 1 + D \cdot D = 1 + D + D^2$ und ist ungleich Null.
Somit kann für die Inverse von $\mathbf{T}(D)$ geschrieben werden (Vertauschung der Diagonalelemente!):
- \[{\boldsymbol{\rm T} }^{-1}(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 & D\\ D & 1+D \end{pmatrix}\hspace{0.05cm}.\]
Das Produkt $\mathbf{T}(D) \cdot \mathbf{T}^{–1}(D)$ ergibt die Einheitsmatrix $\mathbf{I}_2$, und für die dritte Spalte von $\mathbf{G}_{\rm sys}(D)$ gilt:
- \[{\boldsymbol{\rm P} }(D)= {\boldsymbol{\rm T} }^{-1}(D) \cdot {\boldsymbol{\rm Q} }(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 & D\\ D & 1+D \end{pmatrix}\cdot \begin{pmatrix} 1+D\\ 1 \end{pmatrix} \]
- \[\Rightarrow \hspace{0.3cm} {\boldsymbol{\rm P} }(D) = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} (1+D) + D \\ D \cdot (1+D) + (1+D) \end{pmatrix} = \frac{1}{1+D+D^2} \cdot \begin{pmatrix} 1 \\ 1+D^2 \end{pmatrix} \]
- \[\Rightarrow \hspace{0.2cm}{\boldsymbol{\rm G} }_{\rm sys}(D) = \begin{pmatrix} 1 & 0 & \frac{1}{1+D+D^2}\\ 0 & 1 &\frac{1+D^2}{1+D+D^2} \end{pmatrix}\hspace{0.05cm}. \]
Zu klären ist noch, wie das Filter einer solchen gebrochen–rationalen Übertragungsfunktion aussieht.
Filterstruktur bei gebrochen–rationaler Übertragungsfunktion
Hat eine Übertragungsfunktion die Form $G(D) = A(D)/B(D)$, so bezeichnet man das zugehörige Filter als rekursiv.
Bei einem rekursiven Faltungscodierer mit dem Gedächtnis $m$ kann für die beiden Polynome $A(D)$ und $B(D)$ allgemein geschrieben werden:
- \[A(D) = \sum_{l = 0}^{m} a_l \cdot D\hspace{0.05cm}^l = a_0 + a_1 \cdot D + a_2 \cdot D^2 +\ \text{...} \ \hspace{0.05cm} + a_m \cdot D\hspace{0.05cm}^m \hspace{0.05cm},\]
- \[B(D) = 1 + \sum_{l = 1}^{m} b_l \cdot D\hspace{0.05cm}^l = 1 + b_1 \cdot D + b_2 \cdot D^2 + \ \text{...} \ \hspace{0.05cm} + b_m \cdot D\hspace{0.05cm}^m \hspace{0.05cm}.\]
Die Grafik zeigt die entsprechende Filterstruktur in der so genannten Controller Canonical Form:
- Die Koeffizienten $a_0, \ \text{...} \ , \ a_m$ beschreiben den Vorwärtszweig.
- Die Koeffizienten $b_1, \ \text{...} \ , \ b_m$ bilden eine Rückkopplung.
- Alle Koeffizienten sind binär, also $1$ (durchgehende Verbindung) oder $0$ (fehlende Verbindung).
$\text{Beispiel 9:}$ Die rechts skizzierte Filterstruktur lässt sich wie folgt beschreiben:
- \[x_i = w_i + w_{i-2} \hspace{0.05cm},\]
- \[w_i = u_i + w_{i-1}+ w_{i-2} \hspace{0.05cm}.\]
Entsprechend gilt für die $D$–Transformierten:
- \[X(D) =W(D) + W(D) \cdot D^2 =W(D) \cdot \left ( 1+ D^2 \right ) \hspace{0.05cm},\]
- \[W(D) = \hspace{0.08cm} U(D) + W(D) \cdot D+ W(D) \cdot D^2\]
- \[\Rightarrow \hspace{0.3cm} U(D) = W(D) \cdot \left ( 1+ D + D^2 \right ) \hspace{0.05cm}.\]
Somit erhält man für die Übertragungsfunktion dieses Filters:
- \[G(D) = \frac{X(D)}{U(D)} = \frac{1+D^2}{1+D+D^2} \hspace{0.05cm}. \]
Im $\text{Beispiel 8}$ zum äquivalenten systematischen Faltungscode hat sich im unteren Zweig genau dieser Ausdruck ergeben.
Aufgaben zum Kapitel
Aufgabe 3.2: G–Matrix eines Faltungscodierers
Aufgabe 3.2Z: (3, 1, 3)–Faltungscodierer
Aufgabe 3.3: Codesequenzberechnung über U(D) und G(D)
Aufgabe 3.3Z: Faltung und D–Transformation
Aufgabe 3.4: Systematische Faltungscodes
Aufgabe 3.4Z: Äquivalente Faltungscodes?
Aufgabe 3.5: Rekursive Filter für GF(2)