Aufgaben:Aufgabe 5.3Z: Zero-Padding: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
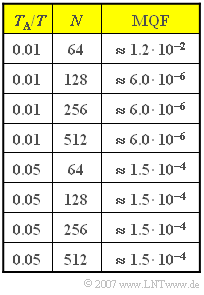
| − | [[Datei:P_ID1146__Sig_Z_5_3_neu.png|right| | + | [[Datei:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$–Werte als Funktion von $T_{\rm A} /T$ und $N$]] |
| − | Wir betrachten die DFT eines Rechteckimpulses $x(t)$ der Höhe $1$ und der Dauer $T$. Damit hat die Spektralfunktion $X(f)$ einen $\sin(f)/f$–förmigen Verlauf. | + | Wir betrachten die DFT eines Rechteckimpulses $x(t)$ der Höhe $A =1$ und der Dauer $T$. Damit hat die Spektralfunktion $X(f)$ einen $\sin(f)/f$–förmigen Verlauf. |
| − | Für diesen Sonderfall soll der Einfluss des DFT–Parameters $N$ analysiert werden, wobei der Stützstellenabstand im Zeitbereich stets $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ betragen soll. | + | Für diesen Sonderfall soll der Einfluss des DFT–Parameters $N$ analysiert werden, wobei der Stützstellenabstand im Zeitbereich stets $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ betragen soll. |
| − | Nebenstehend sind für unterschiedliche Werte von $N$ die sich ergebenden Werte für den | + | Nebenstehend sind für unterschiedliche Werte von $N$ die sich ergebenden Werte für den mittleren quadratischen Fehler $\rm (MQF)$ der Stützwerte im Frequenzbereich angegeben: |
:$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | :$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | ||
\left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | ||
| − | Für $ | + | Für $T_{\rm A}/T = 0.01$ sind somit stets $101$ der DFT–Koeffizienten $d(ν)$ von Null verschieden. |
| + | |||
| + | :* Davon besitzen $99$ den Wert $1$ und die beiden Randkoeffizienten sind jeweils gleich $0.5$. | ||
| + | |||
| + | :* Vergrößert man $N$, so wird das DFT–Koeffizientenfeld mit Nullen aufgefüllt. | ||
| + | |||
| + | :*Man spricht dann von $\text{Zero–Padding}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fehlermöglichkeiten_bei_Anwendung_der_DFT|Fehlermöglichkeiten bei Anwendung der DFT]]. | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Fehlermöglichkeiten_bei_Anwendung_der_DFT|Fehlermöglichkeiten bei Anwendung der DFT]]. |
| − | + | ||
| − | *Die Theorie zu diesem Kapitel ist | + | *Die Theorie zu diesem Kapitel ist im Lernvideo [[Fehlermöglichkeiten_bei_Anwendung_der_DFT_(Lernvideo)|Fehlermöglichkeiten bei Anwendung der DFT]] zusammengefasst. |
| − | + | ||
| + | |||
| Zeile 28: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Aussagen können aus den angegebenen MQF-Werten (gültig für $T_{\rm A}/T = 0.01$ und $N ≥ 128$ | + | {Welche Aussagen können aus den angegebenen MQF-Werten $($gültig für $T_{\rm A}/T = 0.01$ und $N ≥ 128)$ abgeleitet werden? |
|type="[]"} | |type="[]"} | ||
| − | + Der | + | + Der $\rm MQF$–Wert ist hier nahezu unabhängig von $N$. |
| − | - Der | + | - Der $\rm MQF$–Wert wird durch den Abbruchfehler bestimmt. |
| − | + Der | + | + Der $\rm MQF$–Wert wird durch den Aliasingfehler bestimmt. |
| − | {Es gelte $T_{\rm A}/T = 0.01$. Wie groß ist der Abstand $f_{\rm A}$ benachbarter Abtastwerte im Frequenzbereich für $N = 128$ und $N = 512$? | + | {Es gelte $T_{\rm A}/T = 0.01$. Wie groß ist der Abstand $f_{\rm A}$ benachbarter Abtastwerte im Frequenzbereich für $N = 128$ und $N = 512$? |
|type="{}"} | |type="{}"} | ||
| − | $N = 128$: $f_{\rm A} \cdot T $ | + | $N = 128$: $f_{\rm A} \cdot T \ = \ $ { 0.781 3% } |
| − | $N = 512$: $f_{\rm A} \cdot T $ | + | $N = 512$: $f_{\rm A} \cdot T \ = \ $ { 0.196 3% } |
| − | {Was sagt das Produkt $\text{MQF} \cdot f_{\rm A}$ hinsichtlich der DFT–Qualität aus? | + | {Was sagt das Produkt $\text{MQF} \cdot f_{\rm A}$ hinsichtlich der DFT–Qualität aus? |
|type="[]"} | |type="[]"} | ||
| − | + Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt Genauigkeit und Dichte der DFT–Werte. | + | + Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt die Genauigkeit und die Dichte der DFT–Werte. |
| − | - Das Produkt $\text{MQF} \cdot f_{\rm A}$ sollte möglichst groß sein. | + | - Das Produkt $\text{MQF} \cdot f_{\rm A}$ sollte möglichst groß sein. |
| − | {Es wird nun | + | {Es wird nun $N = 128$ fest vorgegeben. Welche Aussagen gelten für den Vergleich der DFT–Ergebnisse mit $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ ? |
|type="[]"} | |type="[]"} | ||
| − | + Mit $T_{\rm A}/T = 0.05$ erhält man eine feinere Frequenzauflösung. | + | + Mit $T_{\rm A}/T = 0.05$ erhält man eine feinere Frequenzauflösung. |
| − | - Mit $T_{\rm A}/T = 0.05$ ist der | + | - Mit $T_{\rm A}/T = 0.05$ ist der $\rm MQF$–Wert kleiner. |
| − | - Mit $T_{\rm A}/T = 0.05$ nimmt der Einfluss des Abbruchfehlers ab. | + | - Mit $T_{\rm A}/T = 0.05$ nimmt der Einfluss des Abbruchfehlers ab. |
| − | + Mit $T_{\rm A}/T = 0.05$ wächst der Einfluss des Aliasingfehlers. | + | + Mit $T_{\rm A}/T = 0.05$ wächst der Einfluss des Aliasingfehlers. |
| − | {Welche Aussagen treffen | + | {Nun gelte $N = 64$. Welche Aussagen treffen für den Vergleich der DFT–Ergebnisse mit $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ zu? |
|type="[]"} | |type="[]"} | ||
| − | + Mit $T_{\rm A}/T = 0.05$ erhält man eine feinere Frequenzauflösung. | + | + Mit $T_{\rm A}/T = 0.05$ erhält man eine feinere Frequenzauflösung. |
| − | + Mit $T_{\rm A}/T = 0.05$ ist der | + | + Mit $T_{\rm A}/T = 0.05$ ist der $\rm MQF$–Wert kleiner. |
| − | + Mit $T_{\rm A}/T = 0.05$ nimmt der Einfluss des Abbruchfehlers ab. | + | + Mit $T_{\rm A}/T = 0.05$ nimmt der Einfluss des Abbruchfehlers ab. |
| − | + Mit $T_{\rm A}/T = 0.05$ wächst der Einfluss des Aliasingfehlers. | + | + Mit $T_{\rm A}/T = 0.05$ wächst der Einfluss des Aliasingfehlers. |
| Zeile 68: | Zeile 79: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: |
| + | *Bereits mit $N = 128$ ist $T_{\rm P} = 1.28 \cdot T$, also größer als die Breite des Rechtecks. | ||
| + | *Somit spielt hier der Abbruchfehler überhaupt keine Rolle. | ||
| + | *Der $\rm MQF$–Wert wird allein durch den Aliasingfehler bestimmt. | ||
| + | *Die Zahlenwerte bestätigen eindeutig, dass $\rm MQF$ (nahezu) unabhängig von $N$ ist. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Aus $T_{\rm A}/T = 0.01$ folgt $f_{\rm P} \cdot T = 100$. | ||
| + | *Die Stützwerte von $X(f)$ liegen also im Bereich $–50 ≤ f \cdot T < +50$. | ||
| + | *Für den Abstand zweier Abtastwerte im Frequenzbereich gilt $f_{\rm A} = f_{\rm P}/N$. Daraus ergeben sich folgende Ergebnisse: | ||
| + | :*$N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$, | ||
| + | :*$N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist die <u>erste Aussage</u>: | ||
| + | *Für $N = 128$ ergibt sich für das Produkt $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. Für $N = 512$ ist das Produkt etwa um den Faktor $4$ kleiner. | ||
| + | *Das heißt: Durch „Zero–Padding” wird keine größere DFT-Genauigkeit erzielt, dafür aber eine feinere „Auflösung” des Frequenzbereichs. | ||
| + | *Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt diese Tatsache; es sollte stets möglichst klein sein. | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1 und 4</u>: |
| − | * | + | *Wegen $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ ergibt sich bei konstantem $N$ immer dann ein kleinerer $f_{\rm A}$–Wert, wenn man $T_{\rm A}$ vergrößert. |
| − | + | *Aus der Tabelle auf der Angabenseite erkennt man, dass damit der mittlere quadratische Fehler $\rm (MQF)$ signifikant $($etwa um den Faktor $400)$ vergrößert wird. | |
| + | *Der Effekt geht auf den Aliasingfehler zurück, da durch den Übergang von $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ die Frequenzperiode um den Faktor $5$ kleiner wird. | ||
| + | *Der Abbruchfehler spielt dagegen beim Rechteckimpuls weiterhin keine Rolle, solange $T_{\rm P} = N \cdot T_{\rm A}$ größer ist als die Impulsdauer $T$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''5 | + | '''(5)''' <u>Alle Aussagen treffen zu</u>: |
| − | * Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf. | + | * Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf. |
| − | *Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert. | + | *Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category:Aufgaben zu Signaldarstellung|^5. Zeit- und | + | [[Category:Aufgaben zu Signaldarstellung|^5. Zeit- und frequenzdiskrete Signaldarstellung^]] |
Aktuelle Version vom 17. Mai 2021, 17:02 Uhr
Wir betrachten die DFT eines Rechteckimpulses $x(t)$ der Höhe $A =1$ und der Dauer $T$. Damit hat die Spektralfunktion $X(f)$ einen $\sin(f)/f$–förmigen Verlauf.
Für diesen Sonderfall soll der Einfluss des DFT–Parameters $N$ analysiert werden, wobei der Stützstellenabstand im Zeitbereich stets $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ betragen soll.
Nebenstehend sind für unterschiedliche Werte von $N$ die sich ergebenden Werte für den mittleren quadratischen Fehler $\rm (MQF)$ der Stützwerte im Frequenzbereich angegeben:
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Für $T_{\rm A}/T = 0.01$ sind somit stets $101$ der DFT–Koeffizienten $d(ν)$ von Null verschieden.
- Davon besitzen $99$ den Wert $1$ und die beiden Randkoeffizienten sind jeweils gleich $0.5$.
- Vergrößert man $N$, so wird das DFT–Koeffizientenfeld mit Nullen aufgefüllt.
- Man spricht dann von $\text{Zero–Padding}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
- Die Theorie zu diesem Kapitel ist im Lernvideo Fehlermöglichkeiten bei Anwendung der DFT zusammengefasst.
Fragebogen
Musterlösung
- Bereits mit $N = 128$ ist $T_{\rm P} = 1.28 \cdot T$, also größer als die Breite des Rechtecks.
- Somit spielt hier der Abbruchfehler überhaupt keine Rolle.
- Der $\rm MQF$–Wert wird allein durch den Aliasingfehler bestimmt.
- Die Zahlenwerte bestätigen eindeutig, dass $\rm MQF$ (nahezu) unabhängig von $N$ ist.
(2) Aus $T_{\rm A}/T = 0.01$ folgt $f_{\rm P} \cdot T = 100$.
- Die Stützwerte von $X(f)$ liegen also im Bereich $–50 ≤ f \cdot T < +50$.
- Für den Abstand zweier Abtastwerte im Frequenzbereich gilt $f_{\rm A} = f_{\rm P}/N$. Daraus ergeben sich folgende Ergebnisse:
- $N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$,
- $N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$.
(3) Richtig ist die erste Aussage:
- Für $N = 128$ ergibt sich für das Produkt $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. Für $N = 512$ ist das Produkt etwa um den Faktor $4$ kleiner.
- Das heißt: Durch „Zero–Padding” wird keine größere DFT-Genauigkeit erzielt, dafür aber eine feinere „Auflösung” des Frequenzbereichs.
- Das Produkt $\text{MQF} \cdot f_{\rm A}$ berücksichtigt diese Tatsache; es sollte stets möglichst klein sein.
(4) Richtig sind die Lösungsvorschläge 1 und 4:
- Wegen $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ ergibt sich bei konstantem $N$ immer dann ein kleinerer $f_{\rm A}$–Wert, wenn man $T_{\rm A}$ vergrößert.
- Aus der Tabelle auf der Angabenseite erkennt man, dass damit der mittlere quadratische Fehler $\rm (MQF)$ signifikant $($etwa um den Faktor $400)$ vergrößert wird.
- Der Effekt geht auf den Aliasingfehler zurück, da durch den Übergang von $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ die Frequenzperiode um den Faktor $5$ kleiner wird.
- Der Abbruchfehler spielt dagegen beim Rechteckimpuls weiterhin keine Rolle, solange $T_{\rm P} = N \cdot T_{\rm A}$ größer ist als die Impulsdauer $T$.
(5) Alle Aussagen treffen zu:
- Mit den Parameterwerten $N = 64$ und $T_{\rm A}/T = 0.01$ tritt ein extrem großer Abbruchfehler auf.
- Alle Zeitkoeffizienten sind hier $1$, so dass die DFT fälschlicherweise ein Gleichsignal anstelle der Rechteckfunktion interpretiert.