Aufgaben:Aufgabe 1.7Z: Systemanalyse: Unterschied zwischen den Versionen
Aus LNTwww
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} | ||
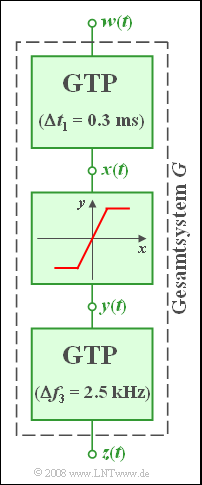
| − | [[Datei:P_ID865__LZI_Z_1_7.png|right|System mit Gaußtiefpässen und nichtlinearer Kennlinie]] Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten: | + | [[Datei:P_ID865__LZI_Z_1_7.png|right|frame|System mit Gaußtiefpässen und nichtlinearer Kennlinie]] |
| + | Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten: | ||
*Die erste Komponente ist ein Gaußtiefpass mit der Impulsantwort | *Die erste Komponente ist ein Gaußtiefpass mit der Impulsantwort | ||
| − | :$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi(t/\Delta t_1)^2}, \hspace{0.5cm} \Delta | + | :$$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm} (t/\Delta t_1)^2}, \hspace{0.5cm} \Delta |
t_1= {0.3\,\rm ms}.$$ | t_1= {0.3\,\rm ms}.$$ | ||
*Danach folgt eine Nichtlinearität mit der Kennlinie | *Danach folgt eine Nichtlinearität mit der Kennlinie | ||
| − | :$$y(t) = \left\{ \begin{array}{c} {8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge {4\,\rm V}}, \\ | + | :$$y(t) = \left\{ \begin{array}{c} +{8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge +{4\,\rm V}}, \\ |
| − | {{-4\,\rm V} < x(t) < {4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$ | + | {{-4\,\rm V} < x(t) < +{4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$ |
| − | :⇒ Das Eingangssignal $x(t)$ der Nichtlinearität wird um den Faktor $2$ verstärkt und – falls nötig – auf den | + | :⇒ Das Eingangssignal $x(t)$ der Nichtlinearität wird um den Faktor $2$ verstärkt und – falls nötig – auf den Bereich $±8 \ \rm V$ begrenzt. |
*Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist: | *Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist: | ||
| − | :$$H_3(f) = {\rm e}^{-\pi(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$ | + | :$$H_3(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$ |
| + | Das Eingangssignal $w(t)$ des Gesamtsystems sei ein Gaußimpuls mit Amplitude $5 \ \rm V$ und variabler (äquivalenter) Dauer $T$: | ||
| + | :$$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$ | ||
| + | Zu untersuchen ist, in welchem Bereich die äquivalente Impulsdauer $T$ dieses Gaußimpulses variieren kann, damit das Gesamtsystem durch den Frequenzgang | ||
| + | :$$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}$$ | ||
| + | vollständig beschrieben wird. Der Index „G” bei Frequenzgang und Bandbreite steht hierbei für „Gesamtsystem”. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''Hinweise:'' | + | |
| − | *Die Aufgabe gehört | + | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen|Einige systemtheoretische Tiefpassfunktionen]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Gau.C3.9F.E2.80.93Tiefpass|Gaußtiefpass]]. | ||
| + | |||
| Zeile 31: | Zeile 39: | ||
{Welche Bedingungen müssen erfüllt sein, damit das Gesamtsystem durch einen einzigen Frequenzgang beschreibbar ist? | {Welche Bedingungen müssen erfüllt sein, damit das Gesamtsystem durch einen einzigen Frequenzgang beschreibbar ist? | ||
|type="[]"} | |type="[]"} | ||
| − | + Es besteht ein linearer Zusammenhang zwischen $w(t)$ und $z(t)$. | + | + Es besteht ein linearer Zusammenhang zwischen $w(t)$ und $z(t)$. |
| − | - $H_3(f)$ muss schmalbandiger sein als $H_1(f)$. | + | - $H_3(f)$ muss schmalbandiger sein als $H_1(f)$. |
| − | + Das Signal $x(t)$ darf betragsmäßig nicht größer sein als $4 \ \rm V$. | + | + Das Signal $x(t)$ darf betragsmäßig nicht größer sein als $4 \ \rm V$. |
| − | {Berechnen Sie den Maximalwert für die äquivalente Impulsdauer $T$, damit die unter (1) genannten Bedingungen erfüllbar sind. | + | {Berechnen Sie den Maximalwert für die äquivalente Impulsdauer $T$, damit die unter '''(1)''' genannten Bedingungen erfüllbar sind. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm max} \ =$ { 0.4 3% } $\ \rm ms$ | + | $T_{\rm max} \ = \ $ { 0.4 3% } $\ \rm ms$ |
| − | {Geben Sie die Parameter des Gesamtfrequenzgangs $H_{\rm G}(f)$ an. | + | {Geben Sie die Parameter des Gesamtfrequenzgangs $H_{\rm G}(f)$ an. |
|type="{}"} | |type="{}"} | ||
| − | $K \=$ { 2 3% } | + | $K \ = \ $ { 2 3% } |
| − | $\Delta f_{\rm G} =$ { 2 3% } $\ \rm kHz$ | + | $\Delta f_{\rm G} = \ $ { 2 3% } $\ \rm kHz$ |
</quiz> | </quiz> | ||
| Zeile 50: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig sind die <u>Antworten1 und 3</u>: | |
| + | *Die erste Aussage ist zutreffend: Nur für ein lineares System kann ein Frequenzgang angegeben werden. | ||
| + | *Damit dies hier möglich ist, darf die Nichtlinearität keine Rolle spielen. | ||
| + | *Das heißt, es muss sicher gestellt sein, dass $|x(t)|$ nicht größer als $4 \ \rm V$ ist. | ||
| + | *Dagegen ist die zweite Aussage nicht zutreffend: Die Bandbreite von $H_3(f)$ hat keinen Einfluss darauf, ob die Nichtlinearität elimimiert werden kann oder nicht. | ||
| − | |||
| − | + | '''(2)''' Der erste Gaußtiefpass wird im Frequenzbereich wie folgt beschrieben: | |
| − | $$ | + | :$$X(f) = W(f) \cdot H_1(f) = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f \cdot T)^2} \cdot {\rm e}^{-\pi(f/\Delta f_1)^2} = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi f^2 (T^2 + \Delta t_1^2)}= {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f/\Delta f_x)^2}.$$ |
| − | + | *Hierbei bezeichnet $Δf_x$ die äquivalente Bandbreite von $X(f)$. | |
| − | $$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$ | + | *Der Signalwert bei $t = 0$ ist gleich der Spektralfläche und gleichzeitig der Maximalwert des Signals: |
| − | + | *Dieser soll nicht größer werden als $4 \ \rm V$: | |
| − | $$ | + | :$$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$ |
| − | \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16} | + | *Daraus folgt durch Koeffizientenvergleich: |
| − | + | :$$\frac{1}{T \cdot \Delta f_x} > \frac{5}{4}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} \frac{1}{T^2 \cdot \Delta f_x^2} > \frac{25}{16} | |
| + | \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16}$$ | ||
| + | :$$ \Rightarrow \hspace{0.1cm}\frac{ \Delta t_1^2}{T^2} > | ||
\frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ | \frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ | ||
\Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow | \Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow | ||
| − | \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}. | + | \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}.$$ |
| − | + | *Die Kontrollrechnung ergibt: | |
| − | $$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = | + | :$$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = {1}/{\Delta t_x}= {2\,\rm kHz}$$ |
| − | $$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$ | + | :$$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$ |
| + | |||
| + | '''(3)''' Die Gaußtiefpässe erfüllen die Bedingung $H_1(f = 0) = H_3(f = 0) = 1$. | ||
| + | *Unter Berücksichtigung der Verstärkung des zweiten Blocks im linearen Bereich erhält man somit für die Gesamtverstärkung: | ||
| + | :$$\underline{K \ = \ 2}.$$ | ||
| − | + | *Für die äquivalente Impulsdauer des Gesamtsystems gilt: | |
| − | + | :$$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm | |
| − | + | kHz}}\right)^2}={0.5\,\rm ms} \; \; \Rightarrow \; \; \Delta f_{\rm G} = {1}/{\Delta t_{\rm G}} \hspace{0.15cm}\underline{= {2\,\rm kHz}}.$$ | |
| − | $$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm | ||
| − | kHz}}\right)^2}={0.5\,\rm ms} | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Zeile 82: | Zeile 96: | ||
| − | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^1.3 | + | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^1.3 Systemtheoretische Tiefpassfunktionen^]] |
Aktuelle Version vom 9. September 2021, 17:43 Uhr
Ein Gesamtsystem $G$ mit Eingang $w(t)$ und Ausgang $z(t)$ besteht aus drei Komponenten:
- Die erste Komponente ist ein Gaußtiefpass mit der Impulsantwort
- $$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm} (t/\Delta t_1)^2}, \hspace{0.5cm} \Delta t_1= {0.3\,\rm ms}.$$
- Danach folgt eine Nichtlinearität mit der Kennlinie
- $$y(t) = \left\{ \begin{array}{c} +{8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge +{4\,\rm V}}, \\ {{-4\,\rm V} < x(t) < +{4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$
- ⇒ Das Eingangssignal $x(t)$ der Nichtlinearität wird um den Faktor $2$ verstärkt und – falls nötig – auf den Bereich $±8 \ \rm V$ begrenzt.
- Am Ende der Kette folgt wieder ein Gaußtiefpass, der durch seinen Frequenzgang gegeben ist:
- $$H_3(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$
Das Eingangssignal $w(t)$ des Gesamtsystems sei ein Gaußimpuls mit Amplitude $5 \ \rm V$ und variabler (äquivalenter) Dauer $T$:
- $$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$
Zu untersuchen ist, in welchem Bereich die äquivalente Impulsdauer $T$ dieses Gaußimpulses variieren kann, damit das Gesamtsystem durch den Frequenzgang
- $$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}$$
vollständig beschrieben wird. Der Index „G” bei Frequenzgang und Bandbreite steht hierbei für „Gesamtsystem”.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige systemtheoretische Tiefpassfunktionen.
- Bezug genommen wird insbesondere auf die Seite Gaußtiefpass.
Fragebogen
Musterlösung
(1) Richtig sind die Antworten1 und 3:
- Die erste Aussage ist zutreffend: Nur für ein lineares System kann ein Frequenzgang angegeben werden.
- Damit dies hier möglich ist, darf die Nichtlinearität keine Rolle spielen.
- Das heißt, es muss sicher gestellt sein, dass $|x(t)|$ nicht größer als $4 \ \rm V$ ist.
- Dagegen ist die zweite Aussage nicht zutreffend: Die Bandbreite von $H_3(f)$ hat keinen Einfluss darauf, ob die Nichtlinearität elimimiert werden kann oder nicht.
(2) Der erste Gaußtiefpass wird im Frequenzbereich wie folgt beschrieben:
- $$X(f) = W(f) \cdot H_1(f) = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f \cdot T)^2} \cdot {\rm e}^{-\pi(f/\Delta f_1)^2} = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi f^2 (T^2 + \Delta t_1^2)}= {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f/\Delta f_x)^2}.$$
- Hierbei bezeichnet $Δf_x$ die äquivalente Bandbreite von $X(f)$.
- Der Signalwert bei $t = 0$ ist gleich der Spektralfläche und gleichzeitig der Maximalwert des Signals:
- Dieser soll nicht größer werden als $4 \ \rm V$:
- $$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$
- Daraus folgt durch Koeffizientenvergleich:
- $$\frac{1}{T \cdot \Delta f_x} > \frac{5}{4}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} \frac{1}{T^2 \cdot \Delta f_x^2} > \frac{25}{16} \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16}$$
- $$ \Rightarrow \hspace{0.1cm}\frac{ \Delta t_1^2}{T^2} > \frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ \Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}.$$
- Die Kontrollrechnung ergibt:
- $$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = {1}/{\Delta t_x}= {2\,\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$
(3) Die Gaußtiefpässe erfüllen die Bedingung $H_1(f = 0) = H_3(f = 0) = 1$.
- Unter Berücksichtigung der Verstärkung des zweiten Blocks im linearen Bereich erhält man somit für die Gesamtverstärkung:
- $$\underline{K \ = \ 2}.$$
- Für die äquivalente Impulsdauer des Gesamtsystems gilt:
- $$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm kHz}}\right)^2}={0.5\,\rm ms} \; \; \Rightarrow \; \; \Delta f_{\rm G} = {1}/{\Delta t_{\rm G}} \hspace{0.15cm}\underline{= {2\,\rm kHz}}.$$