Aufgaben:Aufgabe 4.1Z: Übertragungsmaß: Unterschied zwischen den Versionen
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1798__LZI_Z_4_1.png|right|Kurzer Leitungsabschnitt]] | + | [[Datei:P_ID1798__LZI_Z_4_1.png|right|frame|Kurzer Leitungsabschnitt]] |
| − | Wir gehen von einer homogenen und reflektionsfrei abgeschlossenen Leitung der Länge $l$ aus, so dass für die Spektralfunktion am Ausgang gilt: | + | Wir gehen von einer homogenen und reflektionsfrei abgeschlossenen Leitung der Länge $l$ aus, so dass für die Spektralfunktion am Ausgang gilt: |
| − | $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$ | + | :$$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$ |
| − | Hierbei beschreibt $\gamma(f)$ das Übertragungsmaß einer extrem kurzen Leitung der infinitesimalen Länge $dx$, das mit den Belägen $R'$, $L'$, $G'$ | + | Hierbei beschreibt $\gamma(f)$ das Übertragungsmaß einer extrem kurzen Leitung der infinitesimalen Länge $dx$, das man mit den Belägen $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ und $C\hspace{0.08cm}'$ (siehe Grafik) wie folgt darstellen kann: |
| − | $$\gamma(f) = \sqrt{(R' + {\rm j} \cdot 2\pi f \cdot L') \cdot (G' + {\rm j} \cdot 2\pi f \cdot C')} = | + | :$$\gamma(f) = \sqrt{(R\hspace{0.05cm}' + {\rm j} \cdot 2\pi f \cdot L\hspace{0.05cm}') \cdot (G\hspace{0.08cm}' + {\rm j} \cdot 2\pi f \cdot C\hspace{0.08cm}')} = |
\alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$ | \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$ | ||
| − | Der Realteil von $\gamma(f)$ ergibt das Dämpfungsmaß $\alpha(f)$, der Imaginärteil das Phasenmaß $\beta(f)$. Nach einiger Rechnung kann man für diese Größen schreiben: | + | |
| − | $$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | + | *Der Realteil von $\gamma(f)$ ergibt das Dämpfungsmaß $\alpha(f)$, und |
| − | {1}/{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | *der Imaginärteil das Phasenmaß $\beta(f)$. |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | |
| + | |||
| + | Nach einiger Rechnung kann man für diese Größen schreiben: | ||
| + | :$$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' - \omega^2 \cdot L\hspace{0.05cm}' \cdot C\hspace{0.08cm}'\right)+ | ||
| + | {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} | ||
| + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
f},$$ | f},$$ | ||
| − | $$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R' G' + \omega^2 \cdot L' C'\right)+ | + | :$$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' + \omega^2 \cdot L\hspace{0.05cm}' C\hspace{0.08cm}'\right)+ |
| − | {1}/{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ | + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ |
| − | + | *Bei der Dämpfungsfunktion $a(f)$ ist zusätzlich die Pseudoeinheit „Neper” (Np) hinzuzufügen und bei der Phasenfunktion $b(f)$ „Radian” (rad). | |
| + | *Da die Leitungsbeläge jeweils auf die Leitungslänge bezogen sind, weisen $\alpha(f)$ bzw. $\beta(f)$ die Einheiten „Np/km” bzw. „rad/km” auf. | ||
| + | |||
| + | |||
| + | Eine weitere wichtige Beschreibungsgröße neben $\gamma(f)$ ist der Wellenwiderstand $Z_{\rm W}(f)$, der an jedem Ort den Zusammenhang zwischen Spannung und Strom der beiden laufenden Wellen angibt. Es gilt: | ||
| + | :$$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.08cm}' + {\rm j} \cdot \omega C\hspace{0.08cm}'}} | ||
| + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ | ||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie|Einige Ergebnisse der Leitungstheorie]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_Ergebnisse_der_Leitungstheorie|Einige Ergebnisse der Leitungstheorie]]. |
| − | + | ||
*Verwenden Sie für die numerischen Berechnungen jeweils die Zahlenwerte | *Verwenden Sie für die numerischen Berechnungen jeweils die Zahlenwerte | ||
| − | $$R\hspace{0. | + | :$$R\hspace{0.05cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} |
| − | G\hspace{0. | + | G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} |
| − | 2\pi L' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | + | 2\pi L\hspace{0.03cm}' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} |
| − | 2\pi C\hspace{0. | + | 2\pi C\hspace{0.08cm}' = 200\,\,{\rm nF}/{ {\rm km}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| Zeile 39: | Zeile 50: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie $\alpha(f)$, $\beta(f)$ und $Z_{\rm W}(f)$ für die Frequenz $f = 0$ (Gleichstrom) an. | + | {Geben Sie $\alpha(f)$, $\beta(f)$ und $Z_{\rm W}(f)$ für die Frequenz $f = 0$ ("Gleichstrom") an. |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = | + | $\alpha(f =0) \ =$ { 0.01 3% } $\ \rm Np/km$ |
| − | $\beta(f = | + | $\beta(f = 0) \ =$ { 0. } $\ \rm rad/km$ |
| − | $ | + | $Z_{\rm W}(f = 0) \ =$ { 10000 3% } $\ \rm \Omega$ |
| − | {Berechnen Sie das Dämpfungsmaß $\alpha(f)$ für $f = 100\ \rm kHz$. | + | {Berechnen Sie das Dämpfungsmaß $\alpha(f)$ für $f = 100\ \rm kHz$. |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = 100\ \rm kHz) \ =$ { 0.486 3% } $\ \rm Np/km$ | + | $\alpha(f = 100\ \rm kHz) \ = \ $ { 0.486 3% } $\ \rm Np/km$ |
| − | {Geben Sie für $f → \infty$ | + | {Geben Sie die für $f → \infty$ gültigen Näherungen von $Z_{\rm W}(f)$ und $\alpha(f)$ an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ Z_{\rm W}(f → \infty) \ = \ $ { 100 3% } $\ \rm \Omega$ |
| − | $\alpha(f → \infty)\ =$ { 0.5 3% } $\ \rm Np/km$ | + | $\alpha(f → \infty) \ = \ $ { 0.5 3% } $\ \rm Np/km$ |
| − | {Leiten Sie mit $\omega L' \ll R'$ und $\omega C' \gg G'$ eine $\alpha(f)$– Näherung für (nicht zu) kleine Frequenzen ab. Welches Dämpfungsmaß ergibt sich für $ f = 1 \ \rm kHz$ und $ f = 4 \ \rm kHz$. | + | {Leiten Sie mit $\omega L\hspace{0.03cm}' \ll R\hspace{0.05cm}'$ und $\omega C\hspace{0.08cm}' \gg G\hspace{0.08cm}'$ eine $\alpha(f)$– Näherung für (nicht zu) kleine Frequenzen ab. <br>Welches Dämpfungsmaß ergibt sich für $ f = 1 \ \rm kHz$ und $ f = 4 \ \rm kHz$. |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = 1\ \rm kHz) \ =$ { 0.1 3% } $\ \rm Np/km$ | + | $\alpha(f = 1\ \rm kHz) \ = \ $ { 0.1 3% } $\ \rm Np/km$ |
| − | $\alpha(f = 4\ \rm kHz) \ =$ { 0.2 3% } $\ \rm Np/km$ | + | $\alpha(f = 4\ \rm kHz) \ = \ $ { 0.2 3% } $\ \rm Np/km$ |
| − | {Geben Sie für den gleichen Frequenzbereich eine geeignete Näherung für den Wellenwiderstand $Z_{\rm W}(f)$ an. Welcher Wert ergibt sich für $ f = 1 \ \rm kHz$? | + | {Geben Sie für den gleichen Frequenzbereich eine geeignete Näherung für den Wellenwiderstand $Z_{\rm W}(f)$ an. <br>Welcher Wert ergibt sich für $ f = 1 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}\{ | + | ${\rm Re}\{Z_{\rm W}(f = 1\ \rm kHz)\} \ = \ $ { 500 3% } $\ \rm \Omega$ |
| − | ${\rm Im}\{ | + | ${\rm Im}\{Z_{\rm W}(f = 1\ \rm kHz)\} \ = \ $ { -515--485 } $\ \rm \Omega$ |
| Zeile 74: | Zeile 85: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Setzt man in die gegebenen Gleichungen die Frequenz $f = 0$ ein, so erhält man | + | '''(1)''' Setzt man in die gegebenen Gleichungen die Frequenz $f = 0$ ein, so erhält man |
| − | $$\alpha(f = 0) = [1\,{\rm Np}] \cdot \sqrt{{1}/{2}\cdot R' \cdot G'+ {1}/{2}\cdot R' \cdot | + | :$$\alpha(f = 0) = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{{1}/{2}\hspace{-0.03cm}\cdot \hspace{-0.03cm} R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} |
| − | G'} = [1\,{\rm Np}] \cdot \sqrt{ R' \cdot G'} = [1\,{\rm Np}] \cdot \sqrt{ 100\,{\rm \Omega/km} \cdot 10^{-6}\,{\rm (\Omega \cdot km})^{-1}} | + | G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ 100\,{\rm \Omega/km} \hspace{-0.03cm}\cdot \hspace{-0.03cm} 10^{-6}\,{\rm (\Omega \hspace{-0.03cm}\cdot \hspace{-0.03cm} km})^{-1}} |
\hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} | \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} | ||
}\hspace{0.05cm},$$ | }\hspace{0.05cm},$$ | ||
| − | $$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-{1}/{2}\cdot R' \cdot G'+ {1}/{2}\cdot R' \cdot | + | :$$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-{1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \cdot |
| − | G'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$ | + | G\hspace{0.03cm}'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$ |
| − | :$$Z_{\rm W}(f = 0) = \sqrt{\frac {R'}{G'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm | + | :$$Z_{\rm W}(f = 0) = \sqrt{\frac {R\hspace{0.03cm}'}{G\hspace{0.03cm}'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm |
k \Omega}}\hspace{0.05cm}.$$ | k \Omega}}\hspace{0.05cm}.$$ | ||
| + | |||
Die Gleichsignaldämpfung wird relevant, | Die Gleichsignaldämpfung wird relevant, | ||
| − | *wenn das Nutzsignal im Basisband übertragen werden soll und einen Gleichanteil besitzt, oder | + | *wenn das Nutzsignal im Basisband übertragen werden soll und einen Gleichanteil besitzt, oder |
| − | *wenn der Netzabschluss beim Teilnehmer von der Ortsvermittlungsstelle aus mit Leistung versorgt werden muss (Fernspeisung). | + | *wenn der Netzabschluss beim Teilnehmer von der Ortsvermittlungsstelle aus mit Leistung versorgt werden muss ("Fernspeisung"). |
| + | |||
| − | '''(2)''' Mit $f = 10^{5} \ \rm Hz$ und den angegebenen Werten gilt | + | '''(2)''' Mit $f = 10^{5} \ \rm Hz$ und den angegebenen Werten gilt |
| − | $$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | + | :$$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot |
10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm | 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm | ||
\Omega | \Omega | ||
| − | }{ {\rm km}} \hspace{0.05cm}, | + | }{ {\rm km}} \hspace{0.05cm},\hspace{1.05cm} |
| − | + | f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | |
10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 | 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 | ||
\,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$ | \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$ | ||
Damit ergibt sich für das Dämpfungsmaß in „Np/km”: | Damit ergibt sich für das Dämpfungsmaß in „Np/km”: | ||
| − | $$\alpha(f = 100\,{\rm kHz}) | + | :$$\alpha(f = 100\,{\rm kHz}) |
= \sqrt{ {1}/{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ | = \sqrt{ {1}/{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ | ||
{1}/{2} \cdot \sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} $$ | {1}/{2} \cdot \sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} $$ | ||
| − | $$ \Rightarrow \; \; \alpha(f = 100\,{\rm kHz}) \approx \sqrt{{1}/{2}\cdot \left (10^{-4} - 4 \right)+ | + | :$$ \Rightarrow \; \; \alpha(f = 100\,{\rm kHz}) \approx \sqrt{{1}/{2}\cdot \left (10^{-4} - 4 \right)+ |
{1}/{2}\cdot \sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ | {1}/{2}\cdot \sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ | ||
2}} \hspace{0.15cm}\underline{\approx 0.486 \ {\rm Np/km}} \hspace{0.05cm}.$$ | 2}} \hspace{0.15cm}\underline{\approx 0.486 \ {\rm Np/km}} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' Der Grenzübergang | + | |
| − | $$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) | + | '''(3)''' Der Grenzübergang für $f → \infty$ ergibt sich, wenn man im Zähler $R\hspace{0.03cm}'$ und im Nenner $G\hspace{0.08cm}'$ gegenüber den jeweils zweiten Term vernachlässigt: |
| − | = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} | + | :$$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) |
| − | =\sqrt{\frac {2 \pi L' }{2 \pi C'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } | + | = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C\hspace{0.03cm}'}} |
| + | =\sqrt{\frac {2 \pi L\hspace{0.03cm}' }{2 \pi C\hspace{0.03cm}'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } | ||
{2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$ | {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$ | ||
| − | Die Näherung für die Dämpfungsfunktion ist schwieriger herzuleiten. Ausgehend von | + | *Die Näherung für die Dämpfungsfunktion ist schwieriger herzuleiten. Ausgehend von |
| − | $$\alpha(\omega) = \sqrt{ {1}/{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | + | :$$\alpha(\omega) = \sqrt{ {1}/{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ |
| − | {1}/{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}}$$ | + | {1}/{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot C\hspace{0.03cm}\hspace{0.03cm}'^2)}}$$ |
| − | gilt dann ebenfalls: | + | :gilt dann ebenfalls: |
| − | $$2 \cdot \alpha^2(\omega) = R | + | :$$2 \cdot \alpha^2(\omega) = R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' |
| − | |||
| − | |||
| − | |||
| − | |||
C'\cdot | C'\cdot | ||
| − | \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2}} \hspace{0.1cm} | + | \left [-1 +\sqrt{(1 + \frac{R\hspace{0.03cm}'^2}{ \omega^2 \cdot L\hspace{0.03cm}'^2}) \cdot (1 + \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2})} \hspace{0.1cm} |
\right]$$ | \right]$$ | ||
| − | Über die für kleine $x$ gültige Näherung $\sqrt{1 + x}\approx 1+x/2$ kommt man zum Zwischenergebnis für (unendlich) große Frequenzen: | + | :$$\Rightarrow \; \; 2 \cdot \alpha^2(\omega) \approx R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' |
| − | $$2 \cdot \alpha^2(\omega \rightarrow \infty) = R' G' + \omega^2 \cdot L' | + | C\hspace{0.03cm}'\cdot |
| − | C'\cdot | + | \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2}} \hspace{0.1cm} |
| − | \left [ -1 +1 + {1}/{2} \cdot \left ( \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G'^2}{ \omega^2 \cdot C'^2} | + | \right].$$ |
| + | *Über die für kleine $x$ gültige Näherung $\sqrt{1 + x}\approx 1+x/2$ kommt man zum Zwischenergebnis für (unendlich) große Frequenzen: | ||
| + | :$$2 \cdot \alpha^2(\omega \rightarrow \infty) = R\hspace{0.03cm}' G\hspace{0.05cm}' + \omega^2 \cdot L' | ||
| + | C\hspace{0.05cm}'\cdot | ||
| + | \left [ -1 +1 + {1}/{2} \cdot \left ( \frac{R\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2}+ \frac{G\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2} | ||
\right) \hspace{0.1cm} | \right) \hspace{0.1cm} | ||
\right] $$ | \right] $$ | ||
| − | $$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega \rightarrow \infty) = \frac{2 \cdot R' G' C' L'+ R'\hspace{0.03cm}^2 C'\hspace{0.03cm}^2+ | + | :$$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega \rightarrow \infty) = \frac{2 \cdot R\hspace{0.03cm}' G\hspace{0.03cm}' C\hspace{0.03cm}' L'+ R\hspace{0.03cm}'\hspace{0.03cm}^2 C\hspace{0.03cm}'\hspace{0.03cm}^2+ |
| − | G'\hspace{0.03cm}^2 L'\hspace{0.03cm}^2}{2 \cdot C' L' | + | G\hspace{0.03cm}'\hspace{0.03cm}^2 L\hspace{0.03cm}'\hspace{0.03cm}^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' |
| − | }= | + | }= \frac{(R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}')^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }$$ |
| − | + | :$$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = | |
| − | $$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = | + | {1}/{2}\cdot \frac{R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}'}{\sqrt{ C\hspace{0.03cm}' L\hspace{0.03cm}' }}= |
| − | {1}/{2}\cdot \frac{R' C' + G' L'}{\sqrt{ C' L' }}= | + | {1}/{2}\cdot \left [R\hspace{0.03cm}' \cdot \sqrt{\frac{C\hspace{0.03cm}'}{L\hspace{0.03cm}'}}+G\hspace{0.03cm}' \cdot \sqrt{\frac{L\hspace{0.03cm}'}{C\hspace{0.03cm}'}}\right]\hspace{0.05cm}.$$ |
| − | {1}/{2}\cdot \left [R' \cdot \sqrt{\frac{C'}{L'}}+G' \cdot \sqrt{\frac{L'}{C'}}\right]\hspace{0.05cm}.$$ | + | *Mit den eingesetzten Zahlenwerten ergibt sich |
| − | Mit den eingesetzten Zahlenwerten ergibt sich | + | :$$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) |
| − | $$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) | ||
= {0.5\,{\rm Np/km}}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot | = {0.5\,{\rm Np/km}}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot | ||
\sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] | \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] | ||
| Zeile 142: | Zeile 155: | ||
| − | '''(4)''' Für kleine Frequenzen gilt $\omega L' \ll R'$ und $ \omega C' \gg G'$. | + | |
| − | $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | + | '''(4)''' Für kleine Frequenzen gilt $\omega L\hspace{0.03cm}' \ll R\hspace{0.03cm}'$ und $ \omega C\hspace{0.03cm}' \gg G\hspace{0.03cm}'$. |
| − | \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | *Unter Vernachlässigung des $\omega^2$–Anteils erhält man: |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | :$$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ |
| + | \frac {1}{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2+ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2)}} | ||
| + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
f}$$ | f}$$ | ||
| − | $$ \Rightarrow \hspace{0.3cm} \alpha(f) \approx \sqrt{\frac {R' G'}{2}+ | + | :$$ \Rightarrow \hspace{0.3cm} \alpha(f) \approx \sqrt{\frac {R\hspace{0.03cm}' G\hspace{0.03cm}'}{2}+ |
| − | \frac {R' \cdot \omega C'}{2}} | + | \frac {R\hspace{0.03cm}' \cdot \omega C\hspace{0.03cm}'}{2}} |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | \hspace{0.1cm}\bigg |_{\hspace{0.03cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi |
f} \approx \sqrt{ | f} \approx \sqrt{ | ||
| − | {1}/{2} \cdot f \cdot R' \cdot 2 \pi C'} | + | {1}/{2} \cdot f \cdot R\hspace{0.03cm}' \cdot 2 \pi C\hspace{0.03cm}'} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei ist berücksichtigt, dass der erste Anteil gemäß Teilaufgabe (1) außer bei der Frequenz $f = 0$ | + | *Hierbei ist berücksichtigt, dass der erste Anteil gemäß Teilaufgabe '''(1)''' außer bei der Frequenz $f = 0$ vernachlässigt werden kann. |
| − | *Für die Frequenz $f = 1 \ \rm kHz$ ergibt sich die Näherung | + | *Für die Frequenz $f = 1 \ \rm kHz$ ergibt sich die Näherung |
:$$\alpha(f = 1\,{\rm kHz}) = \sqrt{ | :$$\alpha(f = 1\,{\rm kHz}) = \sqrt{ | ||
{1}/{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} | {1}/{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} | ||
| Zeile 160: | Zeile 175: | ||
\hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} | \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Für die Frequenz $f = | + | *Für die Frequenz $f = 4 \ \rm kHz$ ist das Dämpfungsmaß doppelt so groß: |
:$$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} | :$$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(5)''' Für den Wellenwiderstand gilt bei niedrigen Frequenzen näherungsweise | + | |
| − | $$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot f \cdot 2 \pi L'}{G' + {\rm j} \cdot f \cdot 2 \pi C'}} | + | |
| − | \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R' }{ f \cdot 2 \pi | + | '''(5)''' Für den Wellenwiderstand gilt bei niedrigen Frequenzen näherungsweise: |
| − | C'}}= (1 - {\rm j})\cdot \sqrt{\frac {R' }{ 2 \cdot f \cdot 2 \pi | + | :$$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi L\hspace{0.03cm}'}{G\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi C\hspace{0.03cm}'}} |
| − | C'}}\hspace{0.05cm}.$$ | + | \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R\hspace{0.03cm}' }{ f \cdot 2 \pi |
| − | Mit den angegebenen Leitungsbeschlägen erhält man | + | C\hspace{0.03cm}'}}= (1 - {\rm j})\cdot \sqrt{\frac {R\hspace{0.03cm}' }{ 2 \cdot f \cdot 2 \pi |
| − | $${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} | + | C\hspace{0.03cm}'}}\hspace{0.05cm}.$$ |
| + | *Mit den angegebenen Leitungsbeschlägen erhält man: | ||
| + | :$${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} | ||
\,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm | \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm | ||
\Omega}}\hspace{0.05cm},$$ | \Omega}}\hspace{0.05cm},$$ | ||
| − | $$ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm | + | :$$ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm |
\Omega}}\hspace{0.05cm}.$$ | \Omega}}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 6. November 2021, 17:36 Uhr
Wir gehen von einer homogenen und reflektionsfrei abgeschlossenen Leitung der Länge $l$ aus, so dass für die Spektralfunktion am Ausgang gilt:
- $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
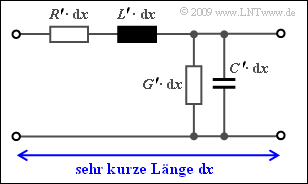
Hierbei beschreibt $\gamma(f)$ das Übertragungsmaß einer extrem kurzen Leitung der infinitesimalen Länge $dx$, das man mit den Belägen $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ und $C\hspace{0.08cm}'$ (siehe Grafik) wie folgt darstellen kann:
- $$\gamma(f) = \sqrt{(R\hspace{0.05cm}' + {\rm j} \cdot 2\pi f \cdot L\hspace{0.05cm}') \cdot (G\hspace{0.08cm}' + {\rm j} \cdot 2\pi f \cdot C\hspace{0.08cm}')} = \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$
- Der Realteil von $\gamma(f)$ ergibt das Dämpfungsmaß $\alpha(f)$, und
- der Imaginärteil das Phasenmaß $\beta(f)$.
Nach einiger Rechnung kann man für diese Größen schreiben:
- $$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' - \omega^2 \cdot L\hspace{0.05cm}' \cdot C\hspace{0.08cm}'\right)+ {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f},$$
- $$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' + \omega^2 \cdot L\hspace{0.05cm}' C\hspace{0.08cm}'\right)+ {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- Bei der Dämpfungsfunktion $a(f)$ ist zusätzlich die Pseudoeinheit „Neper” (Np) hinzuzufügen und bei der Phasenfunktion $b(f)$ „Radian” (rad).
- Da die Leitungsbeläge jeweils auf die Leitungslänge bezogen sind, weisen $\alpha(f)$ bzw. $\beta(f)$ die Einheiten „Np/km” bzw. „rad/km” auf.
Eine weitere wichtige Beschreibungsgröße neben $\gamma(f)$ ist der Wellenwiderstand $Z_{\rm W}(f)$, der an jedem Ort den Zusammenhang zwischen Spannung und Strom der beiden laufenden Wellen angibt. Es gilt:
- $$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.08cm}' + {\rm j} \cdot \omega C\hspace{0.08cm}'}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Ergebnisse der Leitungstheorie.
- Verwenden Sie für die numerischen Berechnungen jeweils die Zahlenwerte
- $$R\hspace{0.05cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} 2\pi L\hspace{0.03cm}' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} 2\pi C\hspace{0.08cm}' = 200\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$\alpha(f = 0) = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{{1}/{2}\hspace{-0.03cm}\cdot \hspace{-0.03cm} R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ 100\,{\rm \Omega/km} \hspace{-0.03cm}\cdot \hspace{-0.03cm} 10^{-6}\,{\rm (\Omega \hspace{-0.03cm}\cdot \hspace{-0.03cm} km})^{-1}} \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} }\hspace{0.05cm},$$
- $$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-{1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$
- $$Z_{\rm W}(f = 0) = \sqrt{\frac {R\hspace{0.03cm}'}{G\hspace{0.03cm}'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm k \Omega}}\hspace{0.05cm}.$$
Die Gleichsignaldämpfung wird relevant,
- wenn das Nutzsignal im Basisband übertragen werden soll und einen Gleichanteil besitzt, oder
- wenn der Netzabschluss beim Teilnehmer von der Ortsvermittlungsstelle aus mit Leistung versorgt werden muss ("Fernspeisung").
(2) Mit $f = 10^{5} \ \rm Hz$ und den angegebenen Werten gilt
- $$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm \Omega }{ {\rm km}} \hspace{0.05cm},\hspace{1.05cm} f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$
Damit ergibt sich für das Dämpfungsmaß in „Np/km”:
- $$\alpha(f = 100\,{\rm kHz}) = \sqrt{ {1}/{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ {1}/{2} \cdot \sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} $$
- $$ \Rightarrow \; \; \alpha(f = 100\,{\rm kHz}) \approx \sqrt{{1}/{2}\cdot \left (10^{-4} - 4 \right)+ {1}/{2}\cdot \sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ 2}} \hspace{0.15cm}\underline{\approx 0.486 \ {\rm Np/km}} \hspace{0.05cm}.$$
(3) Der Grenzübergang für $f → \infty$ ergibt sich, wenn man im Zähler $R\hspace{0.03cm}'$ und im Nenner $G\hspace{0.08cm}'$ gegenüber den jeweils zweiten Term vernachlässigt:
- $$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C\hspace{0.03cm}'}} =\sqrt{\frac {2 \pi L\hspace{0.03cm}' }{2 \pi C\hspace{0.03cm}'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$
- Die Näherung für die Dämpfungsfunktion ist schwieriger herzuleiten. Ausgehend von
- $$\alpha(\omega) = \sqrt{ {1}/{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ {1}/{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot C\hspace{0.03cm}\hspace{0.03cm}'^2)}}$$
- gilt dann ebenfalls:
- $$2 \cdot \alpha^2(\omega) = R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' C'\cdot \left [-1 +\sqrt{(1 + \frac{R\hspace{0.03cm}'^2}{ \omega^2 \cdot L\hspace{0.03cm}'^2}) \cdot (1 + \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2})} \hspace{0.1cm} \right]$$
- $$\Rightarrow \; \; 2 \cdot \alpha^2(\omega) \approx R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' C\hspace{0.03cm}'\cdot \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2}} \hspace{0.1cm} \right].$$
- Über die für kleine $x$ gültige Näherung $\sqrt{1 + x}\approx 1+x/2$ kommt man zum Zwischenergebnis für (unendlich) große Frequenzen:
- $$2 \cdot \alpha^2(\omega \rightarrow \infty) = R\hspace{0.03cm}' G\hspace{0.05cm}' + \omega^2 \cdot L' C\hspace{0.05cm}'\cdot \left [ -1 +1 + {1}/{2} \cdot \left ( \frac{R\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2}+ \frac{G\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2} \right) \hspace{0.1cm} \right] $$
- $$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega \rightarrow \infty) = \frac{2 \cdot R\hspace{0.03cm}' G\hspace{0.03cm}' C\hspace{0.03cm}' L'+ R\hspace{0.03cm}'\hspace{0.03cm}^2 C\hspace{0.03cm}'\hspace{0.03cm}^2+ G\hspace{0.03cm}'\hspace{0.03cm}^2 L\hspace{0.03cm}'\hspace{0.03cm}^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }= \frac{(R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}')^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }$$
- $$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = {1}/{2}\cdot \frac{R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}'}{\sqrt{ C\hspace{0.03cm}' L\hspace{0.03cm}' }}= {1}/{2}\cdot \left [R\hspace{0.03cm}' \cdot \sqrt{\frac{C\hspace{0.03cm}'}{L\hspace{0.03cm}'}}+G\hspace{0.03cm}' \cdot \sqrt{\frac{L\hspace{0.03cm}'}{C\hspace{0.03cm}'}}\right]\hspace{0.05cm}.$$
- Mit den eingesetzten Zahlenwerten ergibt sich
- $$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) = {0.5\,{\rm Np/km}}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] \hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$
(4) Für kleine Frequenzen gilt $\omega L\hspace{0.03cm}' \ll R\hspace{0.03cm}'$ und $ \omega C\hspace{0.03cm}' \gg G\hspace{0.03cm}'$.
- Unter Vernachlässigung des $\omega^2$–Anteils erhält man:
- $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ \frac {1}{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2+ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}$$
- $$ \Rightarrow \hspace{0.3cm} \alpha(f) \approx \sqrt{\frac {R\hspace{0.03cm}' G\hspace{0.03cm}'}{2}+ \frac {R\hspace{0.03cm}' \cdot \omega C\hspace{0.03cm}'}{2}} \hspace{0.1cm}\bigg |_{\hspace{0.03cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f} \approx \sqrt{ {1}/{2} \cdot f \cdot R\hspace{0.03cm}' \cdot 2 \pi C\hspace{0.03cm}'} \hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass der erste Anteil gemäß Teilaufgabe (1) außer bei der Frequenz $f = 0$ vernachlässigt werden kann.
- Für die Frequenz $f = 1 \ \rm kHz$ ergibt sich die Näherung
- $$\alpha(f = 1\,{\rm kHz}) = \sqrt{ {1}/{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} \,\frac{\rm s }{ {\rm \Omega \cdot km}}} \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
- Für die Frequenz $f = 4 \ \rm kHz$ ist das Dämpfungsmaß doppelt so groß:
- $$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
(5) Für den Wellenwiderstand gilt bei niedrigen Frequenzen näherungsweise:
- $$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi L\hspace{0.03cm}'}{G\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi C\hspace{0.03cm}'}} \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R\hspace{0.03cm}' }{ f \cdot 2 \pi C\hspace{0.03cm}'}}= (1 - {\rm j})\cdot \sqrt{\frac {R\hspace{0.03cm}' }{ 2 \cdot f \cdot 2 \pi C\hspace{0.03cm}'}}\hspace{0.05cm}.$$
- Mit den angegebenen Leitungsbeschlägen erhält man:
- $${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm \Omega}}\hspace{0.05cm},$$
- $$ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm \Omega}}\hspace{0.05cm}.$$