Stochastische Signaltheorie/Markovketten: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Betrachtetes Szenario== | ==Betrachtetes Szenario== | ||
| − | Wir betrachten nun | + | <br> |
| − | $$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}...\hspace{0.1cm}, E_\mu , \hspace{0.1cm}...\hspace{0.1cm}, E_M \}.$$ | + | Wir betrachten nun den Fall, dass man ein Zufallsexperiment fortlaufend durchführt und dass zu jedem diskreten Zeitpunkt $(ν = 1, 2, 3, \text{...})$ ein neues Ereignis $E_ν$ eintritt. Hierbei soll gelten: |
| + | [[Datei:P_ID442__Sto_T_1_4_S1_neu.png |right|frame|Mögliche Ereignisse und Ereignisfolge]] | ||
| + | :$$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$ | ||
| − | Diese mathematisch nicht ganz saubere Nomenklatur bedeutet (siehe | + | Diese mathematisch nicht ganz saubere Nomenklatur bedeutet (siehe Grafik): |
| − | *Die $M$ möglichen Ereignisse werden mit dem Laufindex $μ$ durchnummeriert. | + | *Die $M$ möglichen Ereignisse werden mit dem Laufindex $μ$ durchnummeriert. |
| − | *Der Index $ν$ benennt die diskreten Zeitpunkte, zu denen | + | *Der Index $ν$ benennt die diskreten Zeitpunkte, zu denen Ereignisse auftreten. |
| − | |||
| − | Zur einfacheren Darstellung beschränken wir uns im Folgenden auf den Fall $M = 2$ mit der Grundmenge $G = \{ A, B \}$. | + | Zur einfacheren Darstellung beschränken wir uns im Folgenden auf den Fall $M = 2$ mit der Grundmenge $G = \{ A, \ B \}$. Weiter soll gelten: |
| − | * | + | *Die Wahrscheinlichkeit des Ereignisses $E_ν$ kann durchaus von allen vorherigen Ereignissen abhängen – also von den Ereignissen $E_{ν\hspace{0.05cm}-1},\ E_{ν\hspace{0.05cm}-2},\ E_{ν\hspace{0.05cm}-3},$ usw. |
| − | * | + | *Diese Aussage bedeutet auch, dass wir in diesem Kapitel eine '''Ereignisfolge mit inneren statistischen Bindungen''' betrachten. |
| − | |||
| − | + | Dieses Szenario ist ein Sonderfall eines zeit- und wertdiskreten Zufallsprozesses, der im Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Zufallsprozesse|Zufallsprozesse]] noch ausführlich behandelt wird. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | * | + | $\text{Beispiel 1:}$ |
| − | + | Aus einem Kartenstapel mit $32$ Karten (darunter vier Asse) werden nacheinander Karten gezogen. Mit den Ereignissen | |
| + | *$A\text{ :}=$ „die gezogene Karte ist ein Ass”, und | ||
| + | |||
| + | *$B = \overline{A}:=$ „die gezogene Karte ist kein Ass” lauten die Wahrscheinlichkeiten zum Zeitpunkt $ν = 1$: | ||
| + | :$${\rm Pr} (A_{\rm 1}) ={4}/{32}= {1}/{8}, \hspace{0.5cm}{\rm Pr} (B_{\rm 1}) = {28}/{32}= {7}/{8}.$$ | ||
| + | Die Wahrscheinlichkeit ${\rm Pr} (A_{\rm 2})$, dass als zweite Karte $(ν = 2)$ ein Ass gezogen wird, hängt nun davon ab, | ||
| + | *ob zum Zeitpunkt $ν = 1$ ein Ass gezogen wurde ⇒ ${\rm Pr} (A_{\rm 2}) = 3/31 < 1/8$, oder | ||
| + | *ob zum Zeitpunkt $ν = 1$ kein Ass gezogen wurde ⇒ ${\rm Pr} (A_{\rm 2}) = 4/31 > 1/8$. | ||
| − | Auch die Wahrscheinlichkeiten ${\rm Pr} (A_{\nu})$ zu späteren Zeitpunkten $ν$ hängen stets vom Eintreffen bzw. Nichteintreffen aller vorherigen Ereignisse $E_1, ... ,E_{ | + | |
| − | + | Auch die Wahrscheinlichkeiten ${\rm Pr} (A_{\nu})$ zu späteren Zeitpunkten $ν$ hängen stets vom Eintreffen bzw. Nichteintreffen aller vorherigen Ereignisse $E_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} ,E_{ν\hspace{0.05cm}–1}$ ab.}} | |
==Allgemeine Definition einer Markovkette== | ==Allgemeine Definition einer Markovkette== | ||
| + | <br> | ||
In Sonderfällen, die allerdings sehr häufig vorkommen, kann das oben beschriebene Szenario durch eine Markovkette beschrieben werden. | In Sonderfällen, die allerdings sehr häufig vorkommen, kann das oben beschriebene Szenario durch eine Markovkette beschrieben werden. | ||
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | Eine Markovkette $k$-ter Ordnung (englisch: | + | $\text{Definition:}$ |
| − | + | Eine '''Markovkette $k$-ter Ordnung''' (englisch: "Markov Chain") dient als Modell für zeit- und wertdiskrete Vorgänge, bei denen die Ereigniswahrscheinlichkeiten zum Zeitpunkt $ν$ | |
| − | + | # von den vorherigen Ereignissen $E_{ν\hspace{0.05cm}–1}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_{ν\hspace{0.05cm}–k}$ abhängen, und | |
| + | # durch $M^{k+1}$ bedingte Wahrscheinlichkeiten ausgedrückt werden können.}} | ||
| + | Das Schaubild verdeutlicht diesen Sachverhalt am Beispiel $k = 2$. | ||
| + | [[Datei:P_ID444__Sto_T_1_4_S2a_neu.png |right|frame| Markovkette zweiter Ordnung]] | ||
| − | + | Für $M = 2$ gibt es deshalb $2^{k+1}$ solche bedingten Wahrscheinlichkeiten. | |
| + | :$${\rm Pr} ( E_\nu \hspace {0.05cm}\vert \hspace {0.05cm}E_{\nu {\rm -1 } },\hspace {0.15cm}\text{...}\hspace {0.15cm}, E_{\nu { -k } }).$$ | ||
| − | + | Mit $E_{\nu }\in \{ A, B \}, \hspace {0.1cm}\text{...}\hspace {0.15cm}, E_{\nu { -k } } \in \{ A, B \}$ lauten diese: | |
| + | *${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$, | ||
| + | *${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } },B_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, B_{\nu { -2 } })$, | ||
| − | {{ | + | *${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$, |
| − | |||
| − | + | *${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$. | |
| − | |||
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 2:}$ Natürliche Sprachen sind oft durch Markovketten beschreibbar, wobei allerdings die Ordnung $k$ gegen Unendlich strebt. In diesem Beispiel werden Texte allerdings lediglich durch Markovketten zweiter Ordnung angenähert. | |
| − | + | [[Datei:P_ID506__Sto_T_1_4_S2b_neu.png |right|frame| Synthetisch erzeugte Texte (deutsch und englisch)]] | |
| − | |||
| − | + | Die Grafik zeigt beispielhaft zwei synthetisch erzeugte Texte: | |
| − | + | *Der linke Text wurde ausgehend von einer deutschen Buchvorlage mit Bindungen bis zu zweiter Ordnung synthetisch erzeugt. | |
| − | + | *Beim rechten Text wurde eine englische Vorlage verwendet. | |
| − | |||
| − | + | Man erkennt trotz der Beschränkung auf $k = 2$ viele (kurze) deutsche bzw. englische Wörter und auch, dass deutsche Wörter im Mittel länger sind als englische. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Es ergibt sich zwar kein sinnvoller Inhalt, aber die Struktur der jeweiligen Sprache ist durchaus erkennbar. }} | ||
| − | + | ==Markovkette erster Ordnung== | |
| − | + | <br> | |
| − | + | Im Folgenden beschränken wir uns stets auf den Sonderfall $k =1$ . | |
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ | |
| − | + | *Bei einer '''Markovkette erster Ordnung''' (englisch: "First Order Markov Chain") wird lediglich die statistische Bindung zum letzten Ereignis berücksichtigt, die in der Praxis meist auch am stärksten ist. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | *Eine binäre Markovkette erster Ordnung ⇒ Grundmenge $G = \{ A, \ B \}$ weist zum Zeitpunkt $\nu$ folgende Ereigniswahrscheinlichkeiten auf: | ||
| + | :$${\rm Pr}(A_\nu) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) ,$$ | ||
| + | :$${\rm Pr}(B_\nu) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) .$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Zu diesen Gleichungen ist anzumerken: | |
| + | *${\rm Pr}(A_\nu)$ steht als Abkürzung für die Wahrscheinlichkeit, dass zur Zeit $ν$ das Ereignis $E_ν = A = \overline{B}$ auftritt, und es gilt: | ||
| + | :$${\rm Pr}(B_\nu) = 1 - {\rm Pr}(A_\nu).$$ | ||
| + | *Zu jedem Zeitpunkt gibt es vier Übergangswahrscheinlichkeiten ${\rm Pr}(E_ν\hspace{0.05cm} |\hspace{0.05cm} E_{ν–1})$, von denen jedoch nur zwei unabhängig sind, denn es gilt: | ||
| + | :$${\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) = 1 - {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}), \hspace{0.5cm}{\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) = 1 - {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}).$$ | ||
| + | *Durch Verallgemeinerung dieser letzten Aussage gelangt man zu dem Ergebnis, dass es bei einer Markovkette mit $M$ Ereignissen zu jedem Zeitpunkt $ν$ genau $M · (M – 1)$ voneinander unabhängige Übergangswahrscheinlichkeiten gibt. | ||
| − | |||
| − | == | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 3:}$ Mit den vorgegebenen Übergangswahrscheinlichkeiten | |
| + | :$${\rm Pr}(A_ν\hspace{0.05cm}\vert\hspace{0.05cm} A_{ν–1}) = 0.2 \hspace{0.3cm}\text{und}\hspace{0.3cm} {\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 0.4$$ | ||
| + | sind auch die beiden anderen Übergangswahrscheinlichkeiten eindeutig festgelegt: | ||
| + | :$${\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} A_{ν–1}) = 1- 0.2 = 0.8 \hspace{0.3cm}\text{und}\hspace{0.3cm} | ||
| + | {\rm Pr}(A_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 1- 0.4 = 0.6.$$}} | ||
| − | + | ==Homogene Markovketten== | |
| − | + | <br> | |
| − | + | Eine Anwendbarkeit der Markovketten auf praktische Probleme ist meist nur bei weiteren einschränkenden Voraussetzungen gegeben. | |
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | *Sind alle Übergangswahrscheinlichkeiten unabhängig vom betrachteten Zeitpunkt $ν$, so ist die Markovkette '''homogen''' (englisch: "homogeneous"). | ||
| − | + | *Im Fall $M = 2$ verwenden wir hierfür folgende Abkürzungen: | |
| − | * | + | :$${\rm Pr}(A \hspace{0.05cm} \vert \hspace{0.05cm}A) = {\rm Pr}(A_\nu \hspace{0.05cm}\vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}B) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) ,$$ |
| − | $$ | + | :$${\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm}A) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) .$$}} |
| − | |||
| − | |||
| − | |||
| − | $${\rm Pr}( | ||
| − | + | Damit lauten die Ereigniswahrscheinlichkeiten einer binären homogenen Markovkette, die absolute Wahrscheinlichkeiten darstellen im Gegensatz zu den bedingten Übergangswahrscheinlichkeiten : | |
| + | [[Datei:P_ID1444__Sto_T_1_4_S4_neu.png|right|frame| Homogene Markovkette erster Ordnung]] | ||
| + | :$${\rm Pr}(A_\nu) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) ,$$ | ||
| + | :$${\rm Pr}(B_\nu) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) .$$ | ||
| − | {{ | + | Auch aus dem Markovdiagramm kann man ablesen: |
| − | + | *Die Summe der '''abgehenden Pfeile''' eines Ereignisses ist stets Eins: | |
| + | :$${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) =1,$$ | ||
| + | :$${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) =1.$$ | ||
| − | + | *Für die Summen der '''ankommenden Pfeile''' gilt diese Einschränkung nicht: | |
| + | :$$ 0 < {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)< 2,$$ | ||
| + | :$$0 < {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B)< 2.$$ | ||
| + | Sie können das „Einschwingverhalten” der Ereigniswahrscheinlichkeiten einer solchen binären Markovkette mit dem interaktiven SWF–Applet [[Applets:Markovketten|Ereigniswahrscheinlichkeiten einer Markovkette erster Ordnung]] berechnen und anzeigen lassen. | ||
| + | |||
| + | ==Stationäre Wahrscheinlichkeiten== | ||
| + | <br> | ||
| + | Wichtige Eigenschaften von Zufallsprozessen sind [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Station.C3.A4re_Zufallsprozesse|Stationarität]] und [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|Ergodizität]]. Obwohl diese Begriffe erst im vierten Hauptkapitel „Zufallsgrößen mit statistischen Bindungen” definiert werden, wenden wir sie hier bereits vorausgreifend auf Markovketten an. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ | ||
| + | *Sind bei einer Markovkette neben den Übergangswahrscheinlichkeiten auch alle Ereigniswahrscheinlichkeiten unabhängig von der Zeit $ν$, so bezeichnet man die Markovkette als '''stationär''' (englisch: "stationary"). Man verzichtet dann auf den Index $ν$ und schreibt im binären Fall: | ||
| + | :$${\rm Pr}(A_\nu ) = {\rm Pr}(A ) \hspace{0.5 cm} {\rm bzw.} \hspace{0.5 cm} {\rm Pr}(B_\nu ) = {\rm Pr}(B).$$ | ||
| + | *Diese Größen nennt man auch die '''ergodischen Wahrscheinlichkeiten''' der Markovkette.}} | ||
| − | |||
| − | |||
| − | = | + | Stationäre Markovketten weisen die nachfolgend genannten Besonderheiten auf: |
| − | + | *Zur Berechnung der ergodischen Wahrscheinlichkeiten einer binären Markovkette $(M =2)$ kann man folgende Gleichungen verwenden: | |
| − | $$ | + | :$${\rm Pr}(A) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) ,$$ |
| − | + | :$${\rm Pr}(B) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) .$$ | |
| − | + | *Da diese Gleichungen linear voneinander abhängen, darf man nur eine hiervon benutzen. Als zweite Bestimmungsgleichung kann man beispielsweise verwenden: | |
| − | + | :$${\rm Pr}(A) + {\rm Pr}(B) = 1.$$ | |
| − | |||
| − | $${\ | ||
| + | *Die ergodischen Wahrscheinlichkeiten ergeben sich daraus zu | ||
| + | :$${\rm Pr}(A) = \frac {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }\hspace{0.1cm}, $$ | ||
| + | :$${\rm Pr}(B) = \frac {{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }.$$ | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ Wir betrachten eine binäre Markovkette mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten ${\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}A) = 0.4$ und ${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = 0.8$. | ||
| + | [[Datei:P_ID642__Sto_T_1_4_S5_neu.png |right|frame| Zum Einschwingen der Ereigniswahrscheinlichkeiten]] | ||
| + | |||
| + | *Weiterhin setzen wir voraus, dass jede Realisierung dieser Kette zum Startzeitpunkt $ν = 0$ mit dem Ereignis $A$ beginnt. | ||
| + | *Man erhält dann die nachfolgend aufgelisteten Ereigniswahrscheinlichkeiten (mit drei Nachkommastellen): | ||
| − | |||
| − | |||
| + | Es handelt sich hier im strengen Sinne um eine nichtstationäre Markovkette, die jedoch schon nach kurzer Zeit (nahezu) eingeschwungen ist: | ||
| + | *Zu späteren Zeiten $(ν > 5)$ werden die Ereigniswahrscheinlichkeiten ${\rm Pr}(A_ν) \approx 1/4$ und ${\rm Pr}(B_ν) \approx 3/4$ nicht mehr gravierend verändert. | ||
| + | *Aus der Angabe ${\rm Pr}(A_{ν=5}) = 0.250$ und ${\rm Pr}(B_{ν=5}) = 0.750$ sollte allerdings nicht geschlossen werden, dass die Markovkette zum Zeitpunkt $ν = 5$ schon vollkommen eingeschwungen ist. | ||
| + | *Die exakten Werte sind nämlich ${\rm Pr}(A_{ν=5}) = 0.25024$ und ${\rm Pr}(B_{ν=5}) = 0.74976$.}} | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ Bei einer stationären Markovkette treten sehr lange nach Einschalten der Kette $(ν → ∞)$ mit guter Näherung stets die ergodischen Wahrscheinlichkeiten auf, unabhängig von den Startbedingungen ${\rm Pr}(A_0)$ und ${\rm Pr}(B_0) = 1 - {\rm Pr}(A_0)$. | ||
| + | }} | ||
| + | ==Matrix-Vektordarstellung== | ||
| + | <br> | ||
| + | Homogene Markovketten können mit Vektoren und Matrizen sehr kompakt dargestellt werden. Dies empfiehlt sich insbesondere bei mehr als zwei Ereignissen: | ||
| + | :$$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$ | ||
| + | Für die Matrix-Vektorendarstellung verwenden wir folgende Nomenklatur: | ||
| + | *Die $M$ Wahrscheinlichkeiten zum Zeitpunkt $ν$ fassen wir in einem Spaltenvektor zusammen: | ||
| + | :$${\mathbf{p}^{(\nu)}} = \left[ \begin{array}{c} {p_{\rm 1}}^{(\nu)} \\ \dots \\ {p_{M}}^{(\nu)} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{\mu}}^{(\nu)} = {\rm Pr}(E_\nu = E_\mu ).$$ | ||
| + | *Die Übergangswahrscheinlichkeiten werden durch eine $M \times M$-Matrix ausgedrückt: | ||
| + | :$${\mathbf{P}} =\left( p_{ij} \right) = \left[ \begin{array}{cccc} p_{11} & p_{12} & \cdots & p_{1M} \\ p_{21} & p_{22}& \cdots & p_{2M} \\ \dots & \dots & \dots & \dots \\ p_{M1} & p_{M2} & \cdots & p_{MM} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{ij}} = {\rm Pr}(E_{\nu +1 } = E_j \hspace{0.05cm}| \hspace{0.05cm} E_{\nu } = E_i).$$ | ||
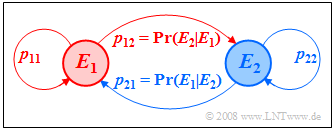
| + | Die nebenstehende Abbildung verdeutlicht diese Nomenklatur am Beispiel $M = 2$. Der neue Ereigniswahrscheinlichkeitsvektor nach einem Schritt lautet: | ||
| + | [[Datei:P_ID448__Sto_T_1_4_S6_neu.png |frame|Zur Bezeichnung der Übergangswahrscheinlichkeiten |right]] | ||
| + | :$${\mathbf{p}^{(\nu + 1)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu )}} .$$ | ||
| + | ${\mathbf{P}^{\rm T}}$ bezeichnet hierbei die zu $\mathbf{P}$ "transponierte Matrix". Nach $n$ Schritten ergibt sich somit | ||
| + | :$${\mathbf{p}^{(\nu +{\it n})}} = \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} .$$ | ||
| − | + | Im Grenzübergang $(n → ∞)$ erreicht man dann stets die Stationarität der Markovkette: | |
| − | $${\mathbf{p}^{(\nu + | + | :$$\lim_{n \to\infty}\hspace{0.1cm}{\mathbf{p}^{(\nu + n)}} = \lim_{n \to\infty} \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} = {\mathbf{p}}_{\rm erg}= \left[ \begin{array}{c} {p_{\rm 1}} \\ \dots \\ {p_{M}} \end{array} \right] .$$ |
| − | ${\mathbf{P} | + | {{BlaueBox|TEXT= |
| − | $${\mathbf{ | + | $\text{Definition:}$ |
| + | *Multipliziert man die Übergangsmatrix ${\mathbf{P} }$ unendlich oft mit sich selbst und benennt das Ergebnis mit ${\mathbf{P} }_{\rm erg}$, so besteht diese Matrix aus $M$ gleichen Zeilen: | ||
| + | :$${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{cccc} p_{1} & p_{2} & \cdots & p_{M} \\ p_{1} & p_{2}& \cdots & p_{M} \\ \dots & \dots & \dots & \dots \\ p_{1} & p_{2} & \cdots & p_{M} \end{array} \right] .$$ | ||
| + | *Die Wahrscheinlichkeiten $p_1, \hspace{0.15cm}\text{...}\hspace{0.1cm},\hspace{0.05cm} p_M$ in jeder dieser Zeilen bezeichnet man als die '''ergodischen Wahrscheinlichkeiten'''. }} | ||
| − | |||
| − | |||
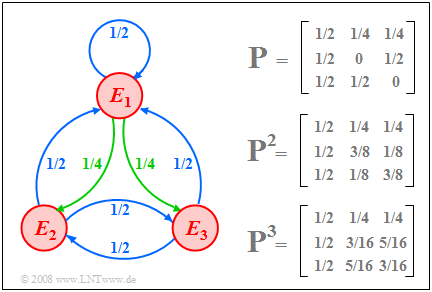
| − | + | [[Datei:P_ID1445__Sto_T_1_4_S6c_neu.png | right|frame|Markovdiagramm mit drei Ereignissen]] | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 5:}$ Wir betrachten beispelhaft eine Markovkette mit den Ereignissen $E_1,\ E_2$ und $E_3$ ⇒ $M=3$. Die Grafik zeigt | ||
| + | *links das Markovdiagramm, | ||
| + | *rechts oben die Übergangsmatrix $\mathbf{P}$ und | ||
| + | *darunter deren Potenzen $\mathbf{P}^2$ und $\mathbf{P}^3$. | ||
| − | {{ | + | Im Markovdiagramm sind alle Übergangswahrscheinlichkeiten mit dem Zahlenwert $1/2$ blau eingezeichnet; grün kennzeichnet die Wahrscheinlichkeit $1/4$. |
| − | + | *Beim Start $(ν =0)$ seien alle Ereignisse gleichwahrscheinlich. Für $ν = 1$ gilt dann: | |
| + | :$${\mathbf{p}^{(1)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(0 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/3 \\ 1/3 \\ 1/3 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$ | ||
| + | :Hieraus ist zu ersehen, dass man von der Matrix $\mathbf{P}$ durch den Austausch der Zeilen und Spalten zur transponierten Matrix ${\mathbf{P}^{\rm T} }$ kommt. | ||
| + | *Zum Zeitpunkt $ν =2$ (und auch zu allen späteren Zeiten) ergeben sich die gleichen Wahrscheinlichkeiten: | ||
| + | :$${\mathbf{p}^{(2)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(1 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$ | ||
| + | :Das bedeutet: Die ergodischen Wahrscheinlichkeiten der drei Ereignisse sind $1/2$ $($für $E_1)$, $1/4$ $($für $E_2)$, und $1/4$ $($für $E_3)$. | ||
| + | *Dieses Ergebnis hätte man auch direkt aus der ergodischen Matrix ablesen können: | ||
| + | :$${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{ccc} 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \end{array} \right] .$$ | ||
| + | *Diese ergibt sich durch fortlaufende Multiplikation der Übergangsmatrix mit sich selbst. Im obigen Bild sind die Potenzen $\mathbf{P}^2$ und $\mathbf{P}^3$ angegeben, die sich der Matrix $\mathbf{P}_{\rm erg}$ annähern.}} | ||
| − | + | ==Aufgaben zum Kapitel== | |
| + | [[Aufgaben:1.6_Übergangswahrscheinlichkeiten|Aufgabe 1.6: Übergangswahrscheinlichkeiten]] | ||
| − | + | [[Aufgaben:1.6Z_Ergodische_Wahrscheinlichkeiten|Aufgabe 1.6Z: Ergodische Wahrscheinlichkeiten]] | |
| − | |||
| − | + | [[Aufgaben:1.7 Ternäre Markovkette|Aufgabe 1.7: Ternäre Markovkette]] | |
| − | |||
| − | + | [[Aufgaben:1.7Z_BARBARA-Generator|Aufgabe 1.7Z: BARBARA-Generator]] | |
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 1. Dezember 2021, 16:26 Uhr
Inhaltsverzeichnis
Betrachtetes Szenario
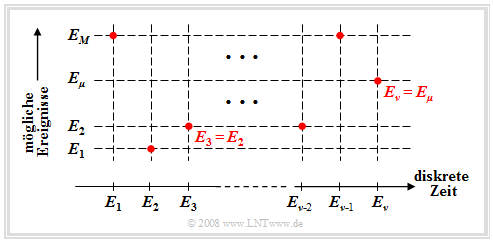
Wir betrachten nun den Fall, dass man ein Zufallsexperiment fortlaufend durchführt und dass zu jedem diskreten Zeitpunkt $(ν = 1, 2, 3, \text{...})$ ein neues Ereignis $E_ν$ eintritt. Hierbei soll gelten:
- $$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$
Diese mathematisch nicht ganz saubere Nomenklatur bedeutet (siehe Grafik):
- Die $M$ möglichen Ereignisse werden mit dem Laufindex $μ$ durchnummeriert.
- Der Index $ν$ benennt die diskreten Zeitpunkte, zu denen Ereignisse auftreten.
Zur einfacheren Darstellung beschränken wir uns im Folgenden auf den Fall $M = 2$ mit der Grundmenge $G = \{ A, \ B \}$. Weiter soll gelten:
- Die Wahrscheinlichkeit des Ereignisses $E_ν$ kann durchaus von allen vorherigen Ereignissen abhängen – also von den Ereignissen $E_{ν\hspace{0.05cm}-1},\ E_{ν\hspace{0.05cm}-2},\ E_{ν\hspace{0.05cm}-3},$ usw.
- Diese Aussage bedeutet auch, dass wir in diesem Kapitel eine Ereignisfolge mit inneren statistischen Bindungen betrachten.
Dieses Szenario ist ein Sonderfall eines zeit- und wertdiskreten Zufallsprozesses, der im Kapitel Zufallsprozesse noch ausführlich behandelt wird.
$\text{Beispiel 1:}$ Aus einem Kartenstapel mit $32$ Karten (darunter vier Asse) werden nacheinander Karten gezogen. Mit den Ereignissen
- $A\text{ :}=$ „die gezogene Karte ist ein Ass”, und
- $B = \overline{A}:=$ „die gezogene Karte ist kein Ass” lauten die Wahrscheinlichkeiten zum Zeitpunkt $ν = 1$:
- $${\rm Pr} (A_{\rm 1}) ={4}/{32}= {1}/{8}, \hspace{0.5cm}{\rm Pr} (B_{\rm 1}) = {28}/{32}= {7}/{8}.$$
Die Wahrscheinlichkeit ${\rm Pr} (A_{\rm 2})$, dass als zweite Karte $(ν = 2)$ ein Ass gezogen wird, hängt nun davon ab,
- ob zum Zeitpunkt $ν = 1$ ein Ass gezogen wurde ⇒ ${\rm Pr} (A_{\rm 2}) = 3/31 < 1/8$, oder
- ob zum Zeitpunkt $ν = 1$ kein Ass gezogen wurde ⇒ ${\rm Pr} (A_{\rm 2}) = 4/31 > 1/8$.
Auch die Wahrscheinlichkeiten ${\rm Pr} (A_{\nu})$ zu späteren Zeitpunkten $ν$ hängen stets vom Eintreffen bzw. Nichteintreffen aller vorherigen Ereignisse $E_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} ,E_{ν\hspace{0.05cm}–1}$ ab.
Allgemeine Definition einer Markovkette
In Sonderfällen, die allerdings sehr häufig vorkommen, kann das oben beschriebene Szenario durch eine Markovkette beschrieben werden.
$\text{Definition:}$ Eine Markovkette $k$-ter Ordnung (englisch: "Markov Chain") dient als Modell für zeit- und wertdiskrete Vorgänge, bei denen die Ereigniswahrscheinlichkeiten zum Zeitpunkt $ν$
- von den vorherigen Ereignissen $E_{ν\hspace{0.05cm}–1}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_{ν\hspace{0.05cm}–k}$ abhängen, und
- durch $M^{k+1}$ bedingte Wahrscheinlichkeiten ausgedrückt werden können.
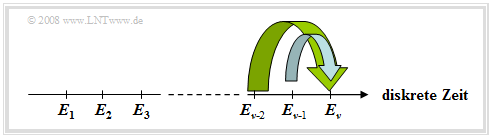
Das Schaubild verdeutlicht diesen Sachverhalt am Beispiel $k = 2$.
Für $M = 2$ gibt es deshalb $2^{k+1}$ solche bedingten Wahrscheinlichkeiten.
- $${\rm Pr} ( E_\nu \hspace {0.05cm}\vert \hspace {0.05cm}E_{\nu {\rm -1 } },\hspace {0.15cm}\text{...}\hspace {0.15cm}, E_{\nu { -k } }).$$
Mit $E_{\nu }\in \{ A, B \}, \hspace {0.1cm}\text{...}\hspace {0.15cm}, E_{\nu { -k } } \in \{ A, B \}$ lauten diese:
- ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$,
- ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } },B_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, B_{\nu { -2 } })$,
- ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$,
- ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$, ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$.
$\text{Beispiel 2:}$ Natürliche Sprachen sind oft durch Markovketten beschreibbar, wobei allerdings die Ordnung $k$ gegen Unendlich strebt. In diesem Beispiel werden Texte allerdings lediglich durch Markovketten zweiter Ordnung angenähert.
Die Grafik zeigt beispielhaft zwei synthetisch erzeugte Texte:
- Der linke Text wurde ausgehend von einer deutschen Buchvorlage mit Bindungen bis zu zweiter Ordnung synthetisch erzeugt.
- Beim rechten Text wurde eine englische Vorlage verwendet.
Man erkennt trotz der Beschränkung auf $k = 2$ viele (kurze) deutsche bzw. englische Wörter und auch, dass deutsche Wörter im Mittel länger sind als englische.
Es ergibt sich zwar kein sinnvoller Inhalt, aber die Struktur der jeweiligen Sprache ist durchaus erkennbar.
Markovkette erster Ordnung
Im Folgenden beschränken wir uns stets auf den Sonderfall $k =1$ .
$\text{Definition:}$
- Bei einer Markovkette erster Ordnung (englisch: "First Order Markov Chain") wird lediglich die statistische Bindung zum letzten Ereignis berücksichtigt, die in der Praxis meist auch am stärksten ist.
- Eine binäre Markovkette erster Ordnung ⇒ Grundmenge $G = \{ A, \ B \}$ weist zum Zeitpunkt $\nu$ folgende Ereigniswahrscheinlichkeiten auf:
- $${\rm Pr}(A_\nu) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) ,$$
- $${\rm Pr}(B_\nu) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) .$$
Zu diesen Gleichungen ist anzumerken:
- ${\rm Pr}(A_\nu)$ steht als Abkürzung für die Wahrscheinlichkeit, dass zur Zeit $ν$ das Ereignis $E_ν = A = \overline{B}$ auftritt, und es gilt:
- $${\rm Pr}(B_\nu) = 1 - {\rm Pr}(A_\nu).$$
- Zu jedem Zeitpunkt gibt es vier Übergangswahrscheinlichkeiten ${\rm Pr}(E_ν\hspace{0.05cm} |\hspace{0.05cm} E_{ν–1})$, von denen jedoch nur zwei unabhängig sind, denn es gilt:
- $${\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) = 1 - {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}), \hspace{0.5cm}{\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) = 1 - {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}).$$
- Durch Verallgemeinerung dieser letzten Aussage gelangt man zu dem Ergebnis, dass es bei einer Markovkette mit $M$ Ereignissen zu jedem Zeitpunkt $ν$ genau $M · (M – 1)$ voneinander unabhängige Übergangswahrscheinlichkeiten gibt.
$\text{Beispiel 3:}$ Mit den vorgegebenen Übergangswahrscheinlichkeiten
- $${\rm Pr}(A_ν\hspace{0.05cm}\vert\hspace{0.05cm} A_{ν–1}) = 0.2 \hspace{0.3cm}\text{und}\hspace{0.3cm} {\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 0.4$$
sind auch die beiden anderen Übergangswahrscheinlichkeiten eindeutig festgelegt:
- $${\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} A_{ν–1}) = 1- 0.2 = 0.8 \hspace{0.3cm}\text{und}\hspace{0.3cm} {\rm Pr}(A_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 1- 0.4 = 0.6.$$
Homogene Markovketten
Eine Anwendbarkeit der Markovketten auf praktische Probleme ist meist nur bei weiteren einschränkenden Voraussetzungen gegeben.
$\text{Definition:}$
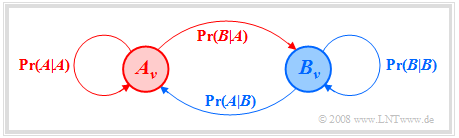
- Sind alle Übergangswahrscheinlichkeiten unabhängig vom betrachteten Zeitpunkt $ν$, so ist die Markovkette homogen (englisch: "homogeneous").
- Im Fall $M = 2$ verwenden wir hierfür folgende Abkürzungen:
- $${\rm Pr}(A \hspace{0.05cm} \vert \hspace{0.05cm}A) = {\rm Pr}(A_\nu \hspace{0.05cm}\vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}B) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) ,$$
- $${\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm}A) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) .$$
Damit lauten die Ereigniswahrscheinlichkeiten einer binären homogenen Markovkette, die absolute Wahrscheinlichkeiten darstellen im Gegensatz zu den bedingten Übergangswahrscheinlichkeiten :
- $${\rm Pr}(A_\nu) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) ,$$
- $${\rm Pr}(B_\nu) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) .$$
Auch aus dem Markovdiagramm kann man ablesen:
- Die Summe der abgehenden Pfeile eines Ereignisses ist stets Eins:
- $${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) =1,$$
- $${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) =1.$$
- Für die Summen der ankommenden Pfeile gilt diese Einschränkung nicht:
- $$ 0 < {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)< 2,$$
- $$0 < {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B)< 2.$$
Sie können das „Einschwingverhalten” der Ereigniswahrscheinlichkeiten einer solchen binären Markovkette mit dem interaktiven SWF–Applet Ereigniswahrscheinlichkeiten einer Markovkette erster Ordnung berechnen und anzeigen lassen.
Stationäre Wahrscheinlichkeiten
Wichtige Eigenschaften von Zufallsprozessen sind Stationarität und Ergodizität. Obwohl diese Begriffe erst im vierten Hauptkapitel „Zufallsgrößen mit statistischen Bindungen” definiert werden, wenden wir sie hier bereits vorausgreifend auf Markovketten an.
$\text{Definition:}$
- Sind bei einer Markovkette neben den Übergangswahrscheinlichkeiten auch alle Ereigniswahrscheinlichkeiten unabhängig von der Zeit $ν$, so bezeichnet man die Markovkette als stationär (englisch: "stationary"). Man verzichtet dann auf den Index $ν$ und schreibt im binären Fall:
- $${\rm Pr}(A_\nu ) = {\rm Pr}(A ) \hspace{0.5 cm} {\rm bzw.} \hspace{0.5 cm} {\rm Pr}(B_\nu ) = {\rm Pr}(B).$$
- Diese Größen nennt man auch die ergodischen Wahrscheinlichkeiten der Markovkette.
Stationäre Markovketten weisen die nachfolgend genannten Besonderheiten auf:
- Zur Berechnung der ergodischen Wahrscheinlichkeiten einer binären Markovkette $(M =2)$ kann man folgende Gleichungen verwenden:
- $${\rm Pr}(A) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) ,$$
- $${\rm Pr}(B) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) .$$
- Da diese Gleichungen linear voneinander abhängen, darf man nur eine hiervon benutzen. Als zweite Bestimmungsgleichung kann man beispielsweise verwenden:
- $${\rm Pr}(A) + {\rm Pr}(B) = 1.$$
- Die ergodischen Wahrscheinlichkeiten ergeben sich daraus zu
- $${\rm Pr}(A) = \frac {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }\hspace{0.1cm}, $$
- $${\rm Pr}(B) = \frac {{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }.$$
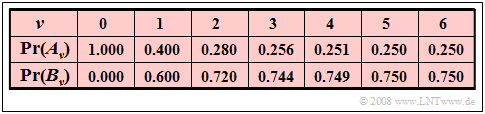
$\text{Beispiel 4:}$ Wir betrachten eine binäre Markovkette mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten ${\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}A) = 0.4$ und ${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = 0.8$.
- Weiterhin setzen wir voraus, dass jede Realisierung dieser Kette zum Startzeitpunkt $ν = 0$ mit dem Ereignis $A$ beginnt.
- Man erhält dann die nachfolgend aufgelisteten Ereigniswahrscheinlichkeiten (mit drei Nachkommastellen):
Es handelt sich hier im strengen Sinne um eine nichtstationäre Markovkette, die jedoch schon nach kurzer Zeit (nahezu) eingeschwungen ist:
- Zu späteren Zeiten $(ν > 5)$ werden die Ereigniswahrscheinlichkeiten ${\rm Pr}(A_ν) \approx 1/4$ und ${\rm Pr}(B_ν) \approx 3/4$ nicht mehr gravierend verändert.
- Aus der Angabe ${\rm Pr}(A_{ν=5}) = 0.250$ und ${\rm Pr}(B_{ν=5}) = 0.750$ sollte allerdings nicht geschlossen werden, dass die Markovkette zum Zeitpunkt $ν = 5$ schon vollkommen eingeschwungen ist.
- Die exakten Werte sind nämlich ${\rm Pr}(A_{ν=5}) = 0.25024$ und ${\rm Pr}(B_{ν=5}) = 0.74976$.
$\text{Fazit:}$ Bei einer stationären Markovkette treten sehr lange nach Einschalten der Kette $(ν → ∞)$ mit guter Näherung stets die ergodischen Wahrscheinlichkeiten auf, unabhängig von den Startbedingungen ${\rm Pr}(A_0)$ und ${\rm Pr}(B_0) = 1 - {\rm Pr}(A_0)$.
Matrix-Vektordarstellung
Homogene Markovketten können mit Vektoren und Matrizen sehr kompakt dargestellt werden. Dies empfiehlt sich insbesondere bei mehr als zwei Ereignissen:
- $$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$
Für die Matrix-Vektorendarstellung verwenden wir folgende Nomenklatur:
- Die $M$ Wahrscheinlichkeiten zum Zeitpunkt $ν$ fassen wir in einem Spaltenvektor zusammen:
- $${\mathbf{p}^{(\nu)}} = \left[ \begin{array}{c} {p_{\rm 1}}^{(\nu)} \\ \dots \\ {p_{M}}^{(\nu)} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{\mu}}^{(\nu)} = {\rm Pr}(E_\nu = E_\mu ).$$
- Die Übergangswahrscheinlichkeiten werden durch eine $M \times M$-Matrix ausgedrückt:
- $${\mathbf{P}} =\left( p_{ij} \right) = \left[ \begin{array}{cccc} p_{11} & p_{12} & \cdots & p_{1M} \\ p_{21} & p_{22}& \cdots & p_{2M} \\ \dots & \dots & \dots & \dots \\ p_{M1} & p_{M2} & \cdots & p_{MM} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{ij}} = {\rm Pr}(E_{\nu +1 } = E_j \hspace{0.05cm}| \hspace{0.05cm} E_{\nu } = E_i).$$
Die nebenstehende Abbildung verdeutlicht diese Nomenklatur am Beispiel $M = 2$. Der neue Ereigniswahrscheinlichkeitsvektor nach einem Schritt lautet:
- $${\mathbf{p}^{(\nu + 1)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu )}} .$$
${\mathbf{P}^{\rm T}}$ bezeichnet hierbei die zu $\mathbf{P}$ "transponierte Matrix". Nach $n$ Schritten ergibt sich somit
- $${\mathbf{p}^{(\nu +{\it n})}} = \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} .$$
Im Grenzübergang $(n → ∞)$ erreicht man dann stets die Stationarität der Markovkette:
- $$\lim_{n \to\infty}\hspace{0.1cm}{\mathbf{p}^{(\nu + n)}} = \lim_{n \to\infty} \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} = {\mathbf{p}}_{\rm erg}= \left[ \begin{array}{c} {p_{\rm 1}} \\ \dots \\ {p_{M}} \end{array} \right] .$$
$\text{Definition:}$
- Multipliziert man die Übergangsmatrix ${\mathbf{P} }$ unendlich oft mit sich selbst und benennt das Ergebnis mit ${\mathbf{P} }_{\rm erg}$, so besteht diese Matrix aus $M$ gleichen Zeilen:
- $${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{cccc} p_{1} & p_{2} & \cdots & p_{M} \\ p_{1} & p_{2}& \cdots & p_{M} \\ \dots & \dots & \dots & \dots \\ p_{1} & p_{2} & \cdots & p_{M} \end{array} \right] .$$
- Die Wahrscheinlichkeiten $p_1, \hspace{0.15cm}\text{...}\hspace{0.1cm},\hspace{0.05cm} p_M$ in jeder dieser Zeilen bezeichnet man als die ergodischen Wahrscheinlichkeiten.
$\text{Beispiel 5:}$ Wir betrachten beispelhaft eine Markovkette mit den Ereignissen $E_1,\ E_2$ und $E_3$ ⇒ $M=3$. Die Grafik zeigt
- links das Markovdiagramm,
- rechts oben die Übergangsmatrix $\mathbf{P}$ und
- darunter deren Potenzen $\mathbf{P}^2$ und $\mathbf{P}^3$.
Im Markovdiagramm sind alle Übergangswahrscheinlichkeiten mit dem Zahlenwert $1/2$ blau eingezeichnet; grün kennzeichnet die Wahrscheinlichkeit $1/4$.
- Beim Start $(ν =0)$ seien alle Ereignisse gleichwahrscheinlich. Für $ν = 1$ gilt dann:
- $${\mathbf{p}^{(1)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(0 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/3 \\ 1/3 \\ 1/3 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$
- Hieraus ist zu ersehen, dass man von der Matrix $\mathbf{P}$ durch den Austausch der Zeilen und Spalten zur transponierten Matrix ${\mathbf{P}^{\rm T} }$ kommt.
- Zum Zeitpunkt $ν =2$ (und auch zu allen späteren Zeiten) ergeben sich die gleichen Wahrscheinlichkeiten:
- $${\mathbf{p}^{(2)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(1 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$
- Das bedeutet: Die ergodischen Wahrscheinlichkeiten der drei Ereignisse sind $1/2$ $($für $E_1)$, $1/4$ $($für $E_2)$, und $1/4$ $($für $E_3)$.
- Dieses Ergebnis hätte man auch direkt aus der ergodischen Matrix ablesen können:
- $${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{ccc} 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \end{array} \right] .$$
- Diese ergibt sich durch fortlaufende Multiplikation der Übergangsmatrix mit sich selbst. Im obigen Bild sind die Potenzen $\mathbf{P}^2$ und $\mathbf{P}^3$ angegeben, die sich der Matrix $\mathbf{P}_{\rm erg}$ annähern.
Aufgaben zum Kapitel
Aufgabe 1.6: Übergangswahrscheinlichkeiten
Aufgabe 1.6Z: Ergodische Wahrscheinlichkeiten
Aufgabe 1.7: Ternäre Markovkette
Aufgabe 1.7Z: BARBARA-Generator