Aufgaben:Aufgabe 4.4: Gaußsche 2D-WDF: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID261__Sto_A_4_4_neu.png|right|]] | + | [[Datei:P_ID261__Sto_A_4_4_neu.png|right|frame|Tabelle: Gaußsche Fehlerfunktionen]] |
| − | + | Wir betrachten zweidimensionale Zufallsgrößen, wobei beide Komponenten stets als mittelwertfrei vorausgesetzt werden. | |
| − | :$$f_{uv}(u, v)= | + | *Die 2D-WDF der Zufallsgröße $(u,\ v)$ lautet: |
| + | :$$f_{uv}(u, v)={1}/{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$ | ||
| − | + | *Von der ebenfalls Gaußschen 2D-Zufallsgröße $(x,\ y)$ sind die folgenden Parameter bekannt: | |
:$$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$ | :$$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$ | ||
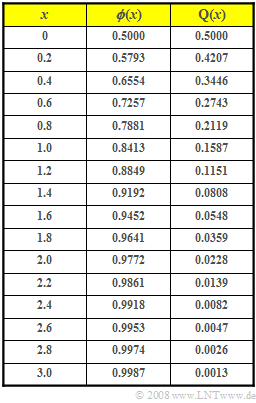
| − | + | Die Werte des Gaußschen Fehlerintegrals ${\rm \phi}(x)$ sowie der Komplementärfunktion ${\rm Q}(x) = 1- {\rm \phi}(x)$ können Sie der nebenstehenden Tabelle entnehmen. | |
| − | |||
| − | |||
| − | :Die | + | |
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | ||
| + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|Gaußverteilte Zufallsgrößen]] | ||
| + | |||
| + | *Weitere Informationen zu dieser Thematik liefert das Lernvideo [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|Gaußsche 2D-Zufallsgrößen]]: | ||
| + | ::Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen, | ||
| + | ::Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen. | ||
| + | |||
| + | |||
| Zeile 21: | Zeile 30: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der Aussagen gelten hinsichtlich der Zufallsgröße ( | + | {Welche der Aussagen gelten hinsichtlich der 2D-Zufallsgröße $(u,\ v)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + Die Zufallsgrößen | + | + Die Zufallsgrößen $u$ und $v$ sind unkorreliert. |
| − | + Die Zufallsgrößen | + | + Die Zufallsgrößen $u$ und $v$ sind statistisch unabhängig. |
| − | {Berechnen Sie die beiden Streuungen | + | {Berechnen Sie die beiden Streuungen $\sigma_u$ und $\sigma_v$. Geben Sie zur Kontrolle den Quotienten der beiden Streuungen ein. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_u/\sigma_v$ | + | $\sigma_u/\sigma_v \ = \ $ { 0.5 3% } |
| − | {Berechnen Sie die Wahrscheinlichkeit, dass | + | {Berechnen Sie die Wahrscheinlichkeit, dass $u$ kleiner als $1$ ist. |
|type="{}"} | |type="{}"} | ||
| − | $Pr(u < 1)$ | + | ${\rm Pr}(u < 1)\ = \ $ { 0.9772 3% } |
| − | {Berechnen Sie die Wahrscheinlichkeit, dass die Zufallsgröße | + | {Berechnen Sie die Wahrscheinlichkeit, dass die Zufallsgröße $u$ kleiner als $1$ und gleichzeitig die Zufallsgröße $v$ größer als $1$ ist. |
|type="{}"} | |type="{}"} | ||
| − | $Pr | + | ${\rm Pr}\big[(u < 1) ∩ (υ > 1)\big]\ = \ $ { 0.1551 3% } |
| − | {Welche der Aussagen sind für die 2D | + | {Welche der Aussagen sind für die 2D–Zufallsgröße $(x,\ y)$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + Die 2D-WDF | + | + Die 2D-WDF $f_{xy}(x,\ y)$ ist außerhalb der Geraden $y = 2x$ stets Null. |
| − | - Für alle Wertepaare auf der Geraden | + | - Für alle Wertepaare auf der Geraden $y = 2x$ gilt $f_{xy}(x,\ y)= 0.5$. |
| − | + Bezüglich der Rand-WDF gilt | + | + Bezüglich der Rand-WDF gilt $f_{x}(x) = f_{u}(u)$ sowie $f_{y}(y) = f_{v}(v)$. |
| − | {Berechnen Sie die Wahrscheinlichkeit, dass | + | {Berechnen Sie die Wahrscheinlichkeit, dass $x$ kleiner als $1$ ist. |
|type="{}"} | |type="{}"} | ||
| − | $Pr(x < 1)$ | + | ${\rm Pr}(x < 1)\ = \ $ { 0.9772 3% } |
| − | {Berechnen Sie nun die Wahrscheinlichkeit, dass die Zufallsgröße | + | {Berechnen Sie nun die Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner als $1$ und gleichzeitig die Zufallsgröße $y$ größer als $1$ ist. |
|type="{}"} | |type="{}"} | ||
| − | $Pr | + | ${\rm Pr}\big[(x < 1) ∩ (y > 1)\big]\ = \ $ { 0.1359 3% } |
| Zeile 64: | Zeile 73: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Beide Aussagen treffen zu</u>: | |
| − | :$$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \sigma_u\sigma_v\sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2})}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v})],$$ | + | *Vergleicht man die gegebene 2D-WDF mit der allgemeingültigen 2D-WDF |
| + | :$$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v \cdot \sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp\left[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2}{\rm )}}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )\right],$$ | ||
| + | |||
| + | :so erkennt man, dass im Exponenten kein Term mit $u \cdot v$ auftritt, was nur bei $\rho_{uv} = 0$ möglich ist. | ||
| + | *Dies bedeutet aber, dass $u$ und $v$ unkorreliert sind. | ||
| + | *Bei Gaußschen Zufallsgrößen folgt aus der Unkorreliertheit aber auch stets die statistische Unabhängigkeit. | ||
| + | |||
| − | |||
| − | + | '''(2)''' Bei statistischer Unabhängigkeit gilt: | |
| − | :$$f_{uv}(u, v) = f_u(u)\cdot f_v(v) | + | :$$f_{uv}(u, v) = f_u(u)\cdot f_v(v) $$ |
| − | :$$f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , \ | + | :$$f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , $$ |
| + | :$$\it f_v{\rm (}v{\rm )}=\frac{{\rm e}^{-{\it v^{\rm 2}}/{{\rm (}{\rm 2}\sigma_v^{\rm 2}{\rm )}}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$ | ||
| − | + | *Durch Koeffizientenvergleich erhält man $\sigma_u = 0.5$ und $\sigma_v = 1$. | |
| − | + | *Der Quotient ist somit $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' Da $u$ eine kontinuierliche Zufallsgröße ist, gilt: | |
| − | :$$\rm Pr | + | :$$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u\rm (1). $$ |
| − | + | *Mit dem Mittelwert $m_u = 0$ und der Streuung $\sigma_u = 0.5$ erhält man: | |
| − | :$$\rm Pr(\it | + | :$$\rm Pr(\it u < \rm 1) = \rm \phi({\rm 1}/{\it\sigma_u})= \rm \phi(\rm 2) \hspace{0.15cm}\underline{=\rm 0.9772}. $$ |
| − | |||
| − | |||
| − | |||
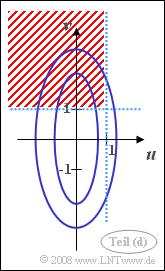
| − | : | + | [[Datei:P_ID265__Sto_A_4_4_d.png|right|frame|Wahrscheinlichkeit: $\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big]$]] |
| + | '''(4)''' Aufgrund der statistischen Unabhängigkeit zwischen $u$ und $v$ gilt: | ||
| + | :$$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$ | ||
| − | + | *Die Wahrscheinlichkeit ${\rm Pr}(u < 1) =0.9772$ wurde bereits berechnet. | |
| + | *Für die zweite Wahrscheinlichkeit ${\rm Pr}(v > 1)$ gilt aus Symmetriegründen: | ||
| + | :$$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm (-1) = \it F_v\rm (-1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$ | ||
| − | :Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden | + | Die Skizze verdeutlicht die vorgegebene Konstellation: |
| + | *Die Höhenlinien der WDF (blau) sind wegen $\sigma_v > \sigma_u$ in vertikaler Richtung gestreckte Ellipsen. | ||
| + | *Rot schraffiert eingezeichnet ist das Gebiet, dessen Wahrscheinlichkeit in dieser Teilaufgabe berechnet werden sollte. | ||
| + | |||
| + | |||
| + | |||
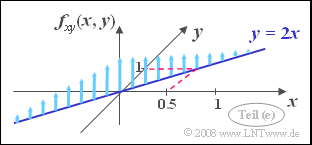
| + | [[Datei:P_ID266__Sto_A_4_4_e.png|right|frame|2D-Diracwand auf der Korrelationsgeraden]] | ||
| + | '''(5)''' Richtig sind <u>der erste und der dritte Lösungsvorschlag</u>: | ||
| + | *Wegen $\rho_{xy} = 1$ besteht ein deterministischer Zusammenhang zwischen $x$ und $y$ | ||
| + | :⇒ Alle Werte liegen auf der Geraden $y =K \cdot x$. | ||
| + | *Aufgrund der Streuungen $\sigma_x = 0.5$ und $\sigma_y = 1$ gilt $K = 2$. | ||
| + | *Auf dieser Geraden $y = 2x$ sind alle WDF-Werte unendlich groß. | ||
| + | *Das bedeutet: Die 2D-WDF ist hier eine „Diracwand”. | ||
| + | *Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden $y = 2x$ gaußverteilt. | ||
| + | *Die Gerade $y = 2x$ stellt gleichzeitig die Korrelationsgerade dar. | ||
| + | *Auch die beiden Randwahrscheinlichkeitsdichten sind Gaußfunktionen, jeweils mit Mittelwert Null. | ||
| + | *Wegen $\sigma_x = \sigma_u$ und $\sigma_y = \sigma_v$ gilt auch: | ||
:$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | :$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | ||
| − | |||
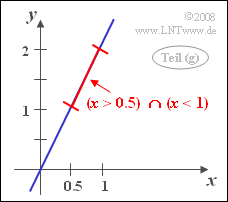
| − | : | + | [[Datei:P_ID274__Sto_A_4_4_g.png|right|frame|Wahrscheinlichkeitsberechnung für die Diracwand]] |
| − | + | '''(6)''' Da die WDF der Zufallsgröße $x$ identisch mit der WDF $f_u(u)$ ist, ergibt sich auch genau die gleiche Wahrscheinlichkeit wie in der Teilaufgabe '''(3)''' berechnet: | |
:$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | :$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(7)''' Das Zufallsereignis $y > 1$ ist identisch mit dem Ereignis $x > 0.5$. | ||
| + | *Damit ist die gesuchte Wahrscheinlichkeit gleich | ||
| + | :$${\rm Pr}\big[(x < 1) ∩ (y > 1)\big] = \rm Pr \big[(\it x < \rm 1) \cap (\it x > \rm 0.5)\big] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$ | ||
| + | *Mit der Streuung $\sigma_x = 0.5$ folgt weiter: | ||
| + | :$$ \rm Pr \big[(\it x > \rm 0.5) \cap (\it x < \rm 1)\big] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 23. Februar 2022, 17:42 Uhr
Wir betrachten zweidimensionale Zufallsgrößen, wobei beide Komponenten stets als mittelwertfrei vorausgesetzt werden.
- Die 2D-WDF der Zufallsgröße $(u,\ v)$ lautet:
- $$f_{uv}(u, v)={1}/{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$
- Von der ebenfalls Gaußschen 2D-Zufallsgröße $(x,\ y)$ sind die folgenden Parameter bekannt:
- $$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$
Die Werte des Gaußschen Fehlerintegrals ${\rm \phi}(x)$ sowie der Komplementärfunktion ${\rm Q}(x) = 1- {\rm \phi}(x)$ können Sie der nebenstehenden Tabelle entnehmen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
- Bezug genommen wird auch auf das Kapitel Gaußverteilte Zufallsgrößen
- Weitere Informationen zu dieser Thematik liefert das Lernvideo Gaußsche 2D-Zufallsgrößen:
- Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen,
- Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen.
Fragebogen
Musterlösung
- Vergleicht man die gegebene 2D-WDF mit der allgemeingültigen 2D-WDF
- $$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v \cdot \sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp\left[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2}{\rm )}}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )\right],$$
- so erkennt man, dass im Exponenten kein Term mit $u \cdot v$ auftritt, was nur bei $\rho_{uv} = 0$ möglich ist.
- Dies bedeutet aber, dass $u$ und $v$ unkorreliert sind.
- Bei Gaußschen Zufallsgrößen folgt aus der Unkorreliertheit aber auch stets die statistische Unabhängigkeit.
(2) Bei statistischer Unabhängigkeit gilt:
- $$f_{uv}(u, v) = f_u(u)\cdot f_v(v) $$
- $$f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , $$
- $$\it f_v{\rm (}v{\rm )}=\frac{{\rm e}^{-{\it v^{\rm 2}}/{{\rm (}{\rm 2}\sigma_v^{\rm 2}{\rm )}}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$
- Durch Koeffizientenvergleich erhält man $\sigma_u = 0.5$ und $\sigma_v = 1$.
- Der Quotient ist somit $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$.
(3) Da $u$ eine kontinuierliche Zufallsgröße ist, gilt:
- $$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u\rm (1). $$
- Mit dem Mittelwert $m_u = 0$ und der Streuung $\sigma_u = 0.5$ erhält man:
- $$\rm Pr(\it u < \rm 1) = \rm \phi({\rm 1}/{\it\sigma_u})= \rm \phi(\rm 2) \hspace{0.15cm}\underline{=\rm 0.9772}. $$
(4) Aufgrund der statistischen Unabhängigkeit zwischen $u$ und $v$ gilt:
- $$\rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$
- Die Wahrscheinlichkeit ${\rm Pr}(u < 1) =0.9772$ wurde bereits berechnet.
- Für die zweite Wahrscheinlichkeit ${\rm Pr}(v > 1)$ gilt aus Symmetriegründen:
- $$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm (-1) = \it F_v\rm (-1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$
- $$\Rightarrow \hspace{0.3cm} \rm Pr\big[(\it u < \rm 1) \cap (\it v > \rm 1)\big] = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$
Die Skizze verdeutlicht die vorgegebene Konstellation:
- Die Höhenlinien der WDF (blau) sind wegen $\sigma_v > \sigma_u$ in vertikaler Richtung gestreckte Ellipsen.
- Rot schraffiert eingezeichnet ist das Gebiet, dessen Wahrscheinlichkeit in dieser Teilaufgabe berechnet werden sollte.
(5) Richtig sind der erste und der dritte Lösungsvorschlag:
- Wegen $\rho_{xy} = 1$ besteht ein deterministischer Zusammenhang zwischen $x$ und $y$
- ⇒ Alle Werte liegen auf der Geraden $y =K \cdot x$.
- Aufgrund der Streuungen $\sigma_x = 0.5$ und $\sigma_y = 1$ gilt $K = 2$.
- Auf dieser Geraden $y = 2x$ sind alle WDF-Werte unendlich groß.
- Das bedeutet: Die 2D-WDF ist hier eine „Diracwand”.
- Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden $y = 2x$ gaußverteilt.
- Die Gerade $y = 2x$ stellt gleichzeitig die Korrelationsgerade dar.
- Auch die beiden Randwahrscheinlichkeitsdichten sind Gaußfunktionen, jeweils mit Mittelwert Null.
- Wegen $\sigma_x = \sigma_u$ und $\sigma_y = \sigma_v$ gilt auch:
- $$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$
(6) Da die WDF der Zufallsgröße $x$ identisch mit der WDF $f_u(u)$ ist, ergibt sich auch genau die gleiche Wahrscheinlichkeit wie in der Teilaufgabe (3) berechnet:
- $$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$
(7) Das Zufallsereignis $y > 1$ ist identisch mit dem Ereignis $x > 0.5$.
- Damit ist die gesuchte Wahrscheinlichkeit gleich
- $${\rm Pr}\big[(x < 1) ∩ (y > 1)\big] = \rm Pr \big[(\it x < \rm 1) \cap (\it x > \rm 0.5)\big] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$
- Mit der Streuung $\sigma_x = 0.5$ folgt weiter:
- $$ \rm Pr \big[(\it x > \rm 0.5) \cap (\it x < \rm 1)\big] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$