Stochastische Signaltheorie/Exponentialverteilte Zufallsgrößen: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Einseitige Exponentialverteilung== | ==Einseitige Exponentialverteilung== | ||
| − | {{Definition} | + | <br> |
| − | Eine kontinuierliche Zufallsgröße $x$ nennt man ( | + | {{BlaueBox|TEXT= |
| − | $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$ | + | $\text{Definition:}$ |
| − | + | Eine kontinuierliche Zufallsgröße $x$ nennt man (einseitig) '''exponentialverteilt''', wenn sie nur nicht–negative Werte annehmen kann und die Wahrscheinlichkeitsdichtefunktion für $x>0$ den folgenden Verlauf hat: | |
| + | :$$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$}} | ||
| − | + | [[Datei: P_ID72__Sto_T_3_6_S1_neu.png |right|frame| WDF und VTF einer exponentialverteilten Zufallsgröße]] | |
| − | |||
| − | |||
| + | Das linke Bild zeigt die "Wahrscheinlichkeitsdichtefunktion" $\rm (WDF)$ einer solchen exponentialverteilten Zufallsgröße $x$. Hervorzuheben ist: | ||
| + | #Je größer der Verteilungsparameter $λ$ ist, um so steiler erfolgt der Abfall. | ||
| + | #Definitionsgemäß gilt $f_{x}(0) = λ/2$, also der Mittelwert aus linksseitigem Grenzwert $(0)$ und rechtsseitigem Grenzwert $(\lambda)$. | ||
| − | + | *Für die "Verteilungsfunktion" $\rm (VTF)$ ⇒ rechte Grafik) erhält man für $r > 0$ durch Integration über die WDF: | |
| + | :$$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$ | ||
| − | + | *Die "Momente" der einseitigen Exponentialverteilung sind allgemein gleich | |
| − | $$ | + | :$$m_k = k!/λ^k.$$ |
| + | *Daraus und aus dem Satz von Steiner ergibt sich für den "Mittelwert" und die "Streuung": | ||
| + | :$$m_1={1}/{\lambda},$$ | ||
| + | :$$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$ | ||
| − | + | {{GraueBox|TEXT= | |
| − | $ | + | $\text{Beispiel 1:}$ Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen, wobei in diesem Zusammenhang auch der Begriff „Lebensdauerverteilung” üblich ist. |
| − | + | # Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit $t$, die bis zum Ausfall einer Komponente vergeht. | |
| + | # Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der [[Stochastische_Signaltheorie/Poissonverteilung|Poissonverteilung]] in Zusammenhang steht.}} | ||
| − | {{ | + | ==Transformation von Zufallsgrößen== |
| − | + | <br> | |
| − | { | + | Zur Erzeugung einer solchen exponentialverteilten Zufallsgröße an einem Digitalrechner kann zum Beispiel eine '''nichtlineare Transformation''' verwendet werden. Das zugrunde liegende Prinzip wird hier zunächst allgemein angegeben. |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Vorgehensweise:}$ Besitzt eine kontinuierliche Zufallsgröße $u$ die WDF $f_{u}(u)$, so gilt für die Wahrscheinlichkeitsdichtefunktion der an der nichtlinearen Kennlinie $x = g(u)$ transformierten Zufallsgröße $x$: | ||
| + | :$$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$ | ||
| + | |||
| + | Hierbei bezeichnet $g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie $g(u)$ und $h(x)$ gibt die Umkehrfunktion zu $g(u)$ an. }} | ||
| + | |||
| + | |||
| + | *Obige Gleichung gilt allerdings nur unter der Voraussetzung, dass die Ableitung $g\hspace{0.03cm}'(u) \ne 0$ ist. | ||
| + | *Bei einer Kennlinie mit horizontalen Abschnitten $(g\hspace{0.05cm}'(u) = 0)$ treten in der WDF zusätzliche Diracfunktionen auf, wenn die Eingangsgröße in dem Bereich Anteile hat. | ||
| + | *Die Gewichte dieser Diracfunktionen sind gleich den Wahrscheinlichkeiten, dass die Eingangsgröße in diesen Bereichen liegt. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID76__Sto_T_3_6_S2_neu.png |frame| Zur Transformation von Zufallsgrößen | rechts]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Gibt man eine zwischen $–2$ und $+2$ dreieckverteilte Zufallsgröße $u$ auf eine Nichtlinerität mit der Kennlinie $x = g(u)$, | ||
| + | *die im Bereich $\vert u \vert ≤ 1$ die Eingangswerte verdreifacht, und | ||
| + | *alle Werte $\vert u \vert > 1$ je nach Vorzeichen auf $x = \pm 3$ abbildet, | ||
| − | |||
| − | |||
| − | + | so ergibt sich die rechts skizzierte WDF $f_{x}(x)$. | |
| − | |||
| − | |||
| − | + | Bitte beachten Sie: | |
| − | + | '''(1)''' Aufgrund der Verstärkung um den Faktor $3$ ist $f_{x}(x)$ um diesen Faktor breiter und niedriger als $f_{u}(u).$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' Die beiden horizontalen Begrenzungen der Kennlinie bei $u = ±1$ führen zu den beiden Diracfunktionen bei $x = ±3$, jeweils mit dem Gewicht $1/8$. | ||
| − | { | + | '''(3)''' Das Gewicht $1/8$ entspricht der grünen Flächen in der WDF $f_{u}(u).$}} |
==Erzeugung einer exponentialverteilten Zufallsgröße== | ==Erzeugung einer exponentialverteilten Zufallsgröße== | ||
| − | + | <br> | |
| − | $$x=\frac{1}{\lambda}\cdot \rm ln(\frac{1}{1-\it u}) | + | {{BlaueBox|TEXT= |
| − | + | $\text{Vorgehensweise:}$ | |
| − | + | Nun wird vorausgesetzt, dass die zu transformierende Zufallsgröße $u$ gleichverteilt zwischen $0$ (inklusive) und $1$ (exklusive) ist. | |
| + | *Außerdem betrachten wir die monoton steigende Kennlinie | ||
| + | :$$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$ | ||
| − | Für $x =$ | + | *Es kann gezeigt werden, dass durch diese Kennlinie $x=g_1(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender WDF entsteht <br>(Herleitung siehe [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Herleitung_der_zugeh.C3.B6rigen_Transformationskennlinie|nächste Seite]]): |
| + | :$$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$ | ||
| + | *Für $x = 0$ ist der WDF-Wert nur halb so groß $(\lambda/2)$. | ||
| + | * Negative $x$-Werte treten nicht auf, da für $0 ≤ u < 1$ das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als $1$.}} | ||
| + | |||
Die gleiche WDF erhält man übrigens mit der monoton fallenden Kennlinie | Die gleiche WDF erhält man übrigens mit der monoton fallenden Kennlinie | ||
| − | $$x=\frac{1}{\lambda}\cdot \rm ln(\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$ | + | :$$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$ |
| + | |||
| + | Bitte beachten Sie: | ||
| + | *Bei einer Rechnerimplementierung entsprechend der ersten Transformationskennlinie $x=g_1(u)$ ist der Wert $u = 1$ auszuschließen. | ||
| + | *Verwendet man die zweite Transformationskennlinie $x=g_2(u)$, so muss dagegen der Wert $u =0$ ausgeschlossen werden. | ||
| + | |||
| + | |||
| + | Das Lernvideo [[Erzeugung_einer_Exponentialverteilung_(Lernvideo)|"Erzeugung einer Exponentialverteilung"]] soll die hier abgeleiteten Transformationen verdeutlichen. | ||
| + | |||
| + | ==Herleitung der zugehörigen Transformationskennlinie== | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Aufgabenstellung:}$ | ||
| + | # Nun wird die bereits auf der letzten Seite verwendete Transformationskennlinie $x = g_1(u)= g(u)$ hergeleitet. | ||
| + | # Diese formt aus der zwischen $0$ und $1$ gleichverteilten Zufallsgröße $u$ mit WDF $f_{u}(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit WDF $f_{x}(x)$: | ||
| + | |||
| + | ::$$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right. \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | ||
| + | f_{x}(x)= \left\{ \begin{array}{*{2}{c} } \lambda\cdot\rm e^{\it -\lambda\hspace{0.03cm} \cdot \hspace{0.03cm} x} & \rm falls\hspace{0.3cm} {\it x} > 0,\\ \lambda/2 & \rm falls\hspace{0.3cm} {\it x} = 0 ,\\ 0 & \rm falls\hspace{0.3cm} {\it x} < 0. \\ \end{array} \right.$$}} | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Problemlösung:}$ | ||
| + | |||
| + | '''(1)''' Ausgehend von der allgemeinen Transformationsgleichung | ||
| + | :$$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$ | ||
| + | erhält man durch Umstellen und Einsetzen der vorgegebenen WDF $f_{ x}(x):$ | ||
| + | :$$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$ | ||
| + | Hierbei gibt $x = g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen. | ||
| + | |||
| + | '''(2)''' Mit dieser Annahme erhält man $\vert g\hspace{0.05cm}'(u)\vert = g\hspace{0.05cm}'(u) = {\rm d}x/{\rm d}u$ und die Differentialgleichung ${\rm d}u = \lambda\ \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}\, {\rm d}x$ mit der Lösung $u = K - {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$ | ||
| + | |||
| + | '''(3)''' Aus der Bedingung, dass die Eingangsgröße $u =0$ zum Ausgangswert $x =0$ führen soll, erhält man für die Konstante $K =1$ und damit $u = 1- {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$ | ||
| + | |||
| + | '''(4)''' Löst man diese Gleichung nach $x$ auf, so ergibt sich die vorne angegebene Gleichung: | ||
| + | :$$x = g_1(u)= \frac{1}{\lambda} \cdot {\rm ln} \left(\frac{1}{1 - u} \right) .$$ | ||
| + | |||
| + | *Bei einer Rechnerimplementierung ist allerdings sicherzustellen, dass für die gleichverteilte Eingangsgröße $u$ der kritische Wert $1$ ausgeschlossen wird. | ||
| + | *Dies wirkt sich jedoch auf das Endergebnis (fast) nicht aus. }} | ||
| + | |||
| + | |||
| + | ==Zweiseitige Exponentialverteilung – Laplaceverteilung== | ||
| + | <br> | ||
| + | In engem Zusammenhang mit der Exponentialverteilung steht die sogenannte [https://de.wikipedia.org/wiki/Laplaceverteilung Laplaceverteilung] mit der Wahrscheinlichkeitsdichtefunktion | ||
| + | :$$f_{x}(x)=\frac{\lambda}{2}\cdot\rm e^{\it -\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} | x|}.$$ | ||
| − | + | Die Laplaceverteilung ist eine ''zweiseitige Exponentialverteilung'', die insbesondere die Amplitudenverteilung von Sprach– und Musiksignalen ausreichend gut approximiert. | |
| + | * Die Momente $k$–ter Ordnung ⇒ $m_k$ der Laplaceverteilung stimmen für geradzahliges $k$ mit denen der Exponentialverteilung überein. | ||
| + | * Für ungeradzahliges $k$ ergibt sich bei der (symmetrischen) Laplaceverteilung dagegen stets $m_k= 0$. | ||
| − | |||
| − | |||
| − | + | Zur Generierung verwendet man eine zwischen $±1$ gleichverteilte Zufallsgröße $v$ (wobei $v = 0$ ausgeschlossen werden muss) und die Transformationskennlinie | |
| − | $$ | + | :$$x=\frac{{\rm sign}(v)}{\lambda}\cdot \rm ln(\it v \rm ).$$ |
| − | |||
| − | |||
| − | + | ''Weitere Hinweise:'' | |
| − | + | *Aus der [[Aufgaben:3.8_Verstärkung_und_Begrenzung| Aufgabe 3.8]] erkennt man weitere Eigenschaften der Laplaceverteilung. | |
| − | Im | + | *Im Lernvideo [[Wahrscheinlichkeit_und_WDF_(Lernvideo)|Wahrscheinlichkeit und WDF]] wird gezeigt, welche Bedeutung die Laplaceverteilung für die Beschreibung von Sprach– und Musiksignalen hat. |
| − | + | *Mit dem Applet [[Applets:WDF,_VTF_und_Momente_spezieller_Verteilungen_(Applet)|WDF, VTF und Momente]] können Sie sich die Kenngrößen $($WDF, VTF, Momente$)$ von Exponential- und Laplaceverteilung anzeigen lassen. | |
| + | *Wir weisen Sie auch auf das Applet [[Applets:Zweidimensionale_Laplace-Zufallsgrößen_(Applet)|Zweidimensionale Laplace-Zufallsgrößen]] hin. | ||
| + | |||
| − | == | + | ==Aufgaben zum Kapitel== |
| + | <br> | ||
| + | [[Aufgaben:3.8 Verstärkung und Begrenzung|Aufgabe 3.8: Verstärkung und Begrenzung]] | ||
| + | |||
| + | [[Aufgaben:Aufgabe_3.8Z:_Kreis(ring)fläche|Aufgabe 3.8Z: Kreis(ring)fläche]] | ||
| + | [[Aufgaben:3.9 Kennlinie für Cosinus-WDF|Aufgabe 3.9: Kennlinie für Cosinus-WDF]] | ||
| − | + | [[Aufgaben:3.9Z Sinustransformation|Aufgabe 3.9Z: Sinustransformation]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 15. Januar 2022, 18:00 Uhr
Inhaltsverzeichnis
Einseitige Exponentialverteilung
$\text{Definition:}$ Eine kontinuierliche Zufallsgröße $x$ nennt man (einseitig) exponentialverteilt, wenn sie nur nicht–negative Werte annehmen kann und die Wahrscheinlichkeitsdichtefunktion für $x>0$ den folgenden Verlauf hat:
- $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$
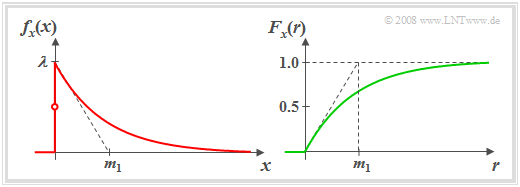
Das linke Bild zeigt die "Wahrscheinlichkeitsdichtefunktion" $\rm (WDF)$ einer solchen exponentialverteilten Zufallsgröße $x$. Hervorzuheben ist:
- Je größer der Verteilungsparameter $λ$ ist, um so steiler erfolgt der Abfall.
- Definitionsgemäß gilt $f_{x}(0) = λ/2$, also der Mittelwert aus linksseitigem Grenzwert $(0)$ und rechtsseitigem Grenzwert $(\lambda)$.
- Für die "Verteilungsfunktion" $\rm (VTF)$ ⇒ rechte Grafik) erhält man für $r > 0$ durch Integration über die WDF:
- $$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$
- Die "Momente" der einseitigen Exponentialverteilung sind allgemein gleich
- $$m_k = k!/λ^k.$$
- Daraus und aus dem Satz von Steiner ergibt sich für den "Mittelwert" und die "Streuung":
- $$m_1={1}/{\lambda},$$
- $$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$
$\text{Beispiel 1:}$ Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen, wobei in diesem Zusammenhang auch der Begriff „Lebensdauerverteilung” üblich ist.
- Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit $t$, die bis zum Ausfall einer Komponente vergeht.
- Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Poissonverteilung in Zusammenhang steht.
Transformation von Zufallsgrößen
Zur Erzeugung einer solchen exponentialverteilten Zufallsgröße an einem Digitalrechner kann zum Beispiel eine nichtlineare Transformation verwendet werden. Das zugrunde liegende Prinzip wird hier zunächst allgemein angegeben.
$\text{Vorgehensweise:}$ Besitzt eine kontinuierliche Zufallsgröße $u$ die WDF $f_{u}(u)$, so gilt für die Wahrscheinlichkeitsdichtefunktion der an der nichtlinearen Kennlinie $x = g(u)$ transformierten Zufallsgröße $x$:
- $$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$
Hierbei bezeichnet $g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie $g(u)$ und $h(x)$ gibt die Umkehrfunktion zu $g(u)$ an.
- Obige Gleichung gilt allerdings nur unter der Voraussetzung, dass die Ableitung $g\hspace{0.03cm}'(u) \ne 0$ ist.
- Bei einer Kennlinie mit horizontalen Abschnitten $(g\hspace{0.05cm}'(u) = 0)$ treten in der WDF zusätzliche Diracfunktionen auf, wenn die Eingangsgröße in dem Bereich Anteile hat.
- Die Gewichte dieser Diracfunktionen sind gleich den Wahrscheinlichkeiten, dass die Eingangsgröße in diesen Bereichen liegt.
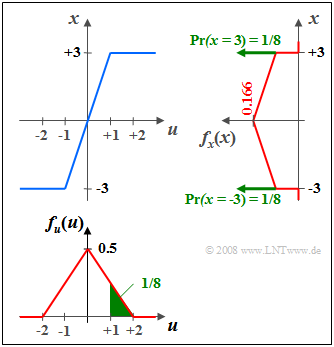
$\text{Beispiel 2:}$ Gibt man eine zwischen $–2$ und $+2$ dreieckverteilte Zufallsgröße $u$ auf eine Nichtlinerität mit der Kennlinie $x = g(u)$,
- die im Bereich $\vert u \vert ≤ 1$ die Eingangswerte verdreifacht, und
- alle Werte $\vert u \vert > 1$ je nach Vorzeichen auf $x = \pm 3$ abbildet,
so ergibt sich die rechts skizzierte WDF $f_{x}(x)$.
Bitte beachten Sie:
(1) Aufgrund der Verstärkung um den Faktor $3$ ist $f_{x}(x)$ um diesen Faktor breiter und niedriger als $f_{u}(u).$
(2) Die beiden horizontalen Begrenzungen der Kennlinie bei $u = ±1$ führen zu den beiden Diracfunktionen bei $x = ±3$, jeweils mit dem Gewicht $1/8$.
(3) Das Gewicht $1/8$ entspricht der grünen Flächen in der WDF $f_{u}(u).$
Erzeugung einer exponentialverteilten Zufallsgröße
$\text{Vorgehensweise:}$ Nun wird vorausgesetzt, dass die zu transformierende Zufallsgröße $u$ gleichverteilt zwischen $0$ (inklusive) und $1$ (exklusive) ist.
- Außerdem betrachten wir die monoton steigende Kennlinie
- $$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$
- Es kann gezeigt werden, dass durch diese Kennlinie $x=g_1(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit folgender WDF entsteht
(Herleitung siehe nächste Seite):
- $$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm f\ddot{u}r}\hspace{0.2cm} {\it x}>0.$$
- Für $x = 0$ ist der WDF-Wert nur halb so groß $(\lambda/2)$.
- Negative $x$-Werte treten nicht auf, da für $0 ≤ u < 1$ das Argument der (natürlichen) Logarithmus–Funktion nicht kleiner wird als $1$.
Die gleiche WDF erhält man übrigens mit der monoton fallenden Kennlinie
- $$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$
Bitte beachten Sie:
- Bei einer Rechnerimplementierung entsprechend der ersten Transformationskennlinie $x=g_1(u)$ ist der Wert $u = 1$ auszuschließen.
- Verwendet man die zweite Transformationskennlinie $x=g_2(u)$, so muss dagegen der Wert $u =0$ ausgeschlossen werden.
Das Lernvideo "Erzeugung einer Exponentialverteilung" soll die hier abgeleiteten Transformationen verdeutlichen.
Herleitung der zugehörigen Transformationskennlinie
$\text{Aufgabenstellung:}$
- Nun wird die bereits auf der letzten Seite verwendete Transformationskennlinie $x = g_1(u)= g(u)$ hergeleitet.
- Diese formt aus der zwischen $0$ und $1$ gleichverteilten Zufallsgröße $u$ mit WDF $f_{u}(u)$ eine einseitig exponentialverteilte Zufallsgröße $x$ mit WDF $f_{x}(x)$:
- $$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm falls\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm falls\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\\ 0 & \rm sonst, \\ \end{array} \right. \hspace{0.5cm}\Rightarrow \hspace{0.5cm} f_{x}(x)= \left\{ \begin{array}{*{2}{c} } \lambda\cdot\rm e^{\it -\lambda\hspace{0.03cm} \cdot \hspace{0.03cm} x} & \rm falls\hspace{0.3cm} {\it x} > 0,\\ \lambda/2 & \rm falls\hspace{0.3cm} {\it x} = 0 ,\\ 0 & \rm falls\hspace{0.3cm} {\it x} < 0. \\ \end{array} \right.$$
$\text{Problemlösung:}$
(1) Ausgehend von der allgemeinen Transformationsgleichung
- $$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$
erhält man durch Umstellen und Einsetzen der vorgegebenen WDF $f_{ x}(x):$
- $$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$
Hierbei gibt $x = g\hspace{0.05cm}'(u)$ die Ableitung der Kennlinie an, die wir als monoton steigend voraussetzen.
(2) Mit dieser Annahme erhält man $\vert g\hspace{0.05cm}'(u)\vert = g\hspace{0.05cm}'(u) = {\rm d}x/{\rm d}u$ und die Differentialgleichung ${\rm d}u = \lambda\ \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}\, {\rm d}x$ mit der Lösung $u = K - {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$
(3) Aus der Bedingung, dass die Eingangsgröße $u =0$ zum Ausgangswert $x =0$ führen soll, erhält man für die Konstante $K =1$ und damit $u = 1- {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$
(4) Löst man diese Gleichung nach $x$ auf, so ergibt sich die vorne angegebene Gleichung:
- $$x = g_1(u)= \frac{1}{\lambda} \cdot {\rm ln} \left(\frac{1}{1 - u} \right) .$$
- Bei einer Rechnerimplementierung ist allerdings sicherzustellen, dass für die gleichverteilte Eingangsgröße $u$ der kritische Wert $1$ ausgeschlossen wird.
- Dies wirkt sich jedoch auf das Endergebnis (fast) nicht aus.
Zweiseitige Exponentialverteilung – Laplaceverteilung
In engem Zusammenhang mit der Exponentialverteilung steht die sogenannte Laplaceverteilung mit der Wahrscheinlichkeitsdichtefunktion
- $$f_{x}(x)=\frac{\lambda}{2}\cdot\rm e^{\it -\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} | x|}.$$
Die Laplaceverteilung ist eine zweiseitige Exponentialverteilung, die insbesondere die Amplitudenverteilung von Sprach– und Musiksignalen ausreichend gut approximiert.
- Die Momente $k$–ter Ordnung ⇒ $m_k$ der Laplaceverteilung stimmen für geradzahliges $k$ mit denen der Exponentialverteilung überein.
- Für ungeradzahliges $k$ ergibt sich bei der (symmetrischen) Laplaceverteilung dagegen stets $m_k= 0$.
Zur Generierung verwendet man eine zwischen $±1$ gleichverteilte Zufallsgröße $v$ (wobei $v = 0$ ausgeschlossen werden muss) und die Transformationskennlinie
- $$x=\frac{{\rm sign}(v)}{\lambda}\cdot \rm ln(\it v \rm ).$$
Weitere Hinweise:
- Aus der Aufgabe 3.8 erkennt man weitere Eigenschaften der Laplaceverteilung.
- Im Lernvideo Wahrscheinlichkeit und WDF wird gezeigt, welche Bedeutung die Laplaceverteilung für die Beschreibung von Sprach– und Musiksignalen hat.
- Mit dem Applet WDF, VTF und Momente können Sie sich die Kenngrößen $($WDF, VTF, Momente$)$ von Exponential- und Laplaceverteilung anzeigen lassen.
- Wir weisen Sie auch auf das Applet Zweidimensionale Laplace-Zufallsgrößen hin.
Aufgaben zum Kapitel
Aufgabe 3.8: Verstärkung und Begrenzung
Aufgabe 3.8Z: Kreis(ring)fläche
Aufgabe 3.9: Kennlinie für Cosinus-WDF
Aufgabe 3.9Z: Sinustransformation