Aufgaben:Aufgabe 3.6Z: Prüfungskorrektur: Unterschied zwischen den Versionen
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
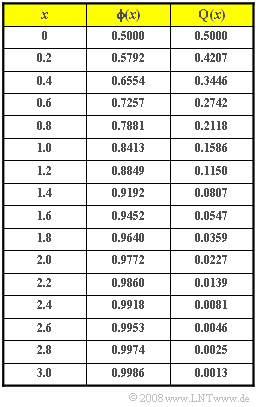
| − | [[Datei:P_ID148__Sto_Z_3_6.png|right| | + | [[Datei:P_ID148__Sto_Z_3_6.png|right|frame|Tabelle für ${\rm \phi}(x)$ und ${\rm Q}(x)$]] |
| − | An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. | + | An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. Ab der Note „4.0” gilt die Prüfung als bestanden. Die Prüfungsordnung sieht folgende Noten vor: |
| − | *Die maximal erreichbare Punktzahl | + | :$$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$ |
| − | *Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Gaußverteilung]] mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$. | + | Weiter ist bei der Aufgabe zu berücksichtigen: |
| − | *Bei der Korrektur wurden nicht nur ganze | + | *Die maximal erreichbare Punktzahl beträgt $100$. Der beste Student erreichte $88$ Punkte. |
| + | *Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Gaußverteilung]] mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$. | ||
| + | *Bei der Korrektur wurden nicht nur ganze Punktzahlen vergeben, sondern auch (beliebige) Zwischenwerte, so dass man die Zufallsgröße $z$ mit guter Näherung als „kontinuierlich” auffassen kann. | ||
| − | |||
| − | :$$1.0 | + | Für die Bewertung werden als Richtlinien vorgegeben: |
| + | *Auch mit sechs Punkten weniger als der Beste $($also ab $82$ Punkten$)$ soll man „1.0” bekommen. | ||
| + | *Hat man $46\%$ der Gesamtpunktzahl erreicht, so hat man die Prüfung bestanden. | ||
| + | *Die Punkte/Noten-Zuordnung soll linear erfolgen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilte Zufallsgrößen]]. |
| − | * | + | *Gerade im Schulbereich wird die „Gaußverteilung” oft als „Normalverteilung” bezeichnet. Dies ist nicht ganz korrekt: |
| − | + | : Eine normalverteilte Zufallsgröße $z$ hat zwar eine Gaußsche WDF und VTF, jedoch stets mit Mittelwert $m_z = 0$ und Streuung $\sigma_z = 1$. | |
| − | : | ||
| − | |||
| − | |||
| Zeile 35: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Kriterien sind bei der Aufgabenerstellung | + | {Welche Kriterien sind bei der Aufgabenerstellung zu beachten, damit die Punktezahl „etwa eine Normalverteilung” ergeben wird? |
|type="[]"} | |type="[]"} | ||
+ Es gibt viele Prüfungsteilnehmer. | + Es gibt viele Prüfungsteilnehmer. | ||
- Die Teilaufgaben hängen in starkem Maße voneinander ab. | - Die Teilaufgaben hängen in starkem Maße voneinander ab. | ||
+ Es gibt viele unabhängige Aufgaben. | + Es gibt viele unabhängige Aufgaben. | ||
| − | - Die Prüfung besteht aus einer Frage mit Ja/Nein-Antwort. | + | - Die Prüfung besteht aus einer einzigen Frage mit Ja/Nein-Antwort. |
{Wieviele Teilnehmer werden voraussichtlich mit „1.0“ abschließen? | {Wieviele Teilnehmer werden voraussichtlich mit „1.0“ abschließen? | ||
|type="{}"} | |type="{}"} | ||
| − | $N_\text{1.0}$ | + | $N_\text{1.0} \ = \ $ { 14 3% } |
| − | {Wieviele Teilnehmer werden wohl nicht bestehen? Berücksichtigen Sie, dass | + | {Wieviele Teilnehmer werden die Prüfung wohl nicht bestehen? Berücksichtigen Sie, dass man $z$ als kontinuierliche Zufallsgröße auffassen kann. |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{4.3 ... 5.0}$ | + | $N_\text{4.3 ... 5.0} \ = \ $ { 81 3% } |
| − | {Legen Sie die Punkte/Noten–Zuordnung fest. Ab wann bekommt man eine „3.0“? Wieviele Prüfungsteilnehmer werden diese Note erhalten? | + | {Legen Sie die Punkte/Noten–Zuordnung fest. Ab wann bekommt man eine „3.0“? Wieviele Prüfungsteilnehmer werden diese Note erhalten? |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{3.0}$ | + | $N_\text{3.0} \ = \ $ { 159 3% } |
| − | {Wieviele Teilnehmer erhalten voraussichtlich die Note „2.7“? Begründen Sie, warum genau so viele Prüflinge die Note „3.3“ bekommen werden. | + | {Wieviele Teilnehmer erhalten voraussichtlich die Note „2.7“? Begründen Sie, warum genau so viele Prüflinge die Note „3.3“ bekommen werden. |
|type="{}"} | |type="{}"} | ||
| − | $N_\text{2.7}$ | + | $N_\text{2.7} \ = \ $ { 146 3% } |
| − | {Welche Mittelnote wird sich bei dieser Prüfung ergeben? Berücksichtigen Sie zur Lösung dieser Teilaufgabe das Ergebnis von ( | + | {Welche Mittelnote wird sich bei dieser Prüfung ergeben? Berücksichtigen Sie zur Lösung dieser Teilaufgabe das Ergebnis von Teilaufgabe '''(5)'''. |
|type="{}"} | |type="{}"} | ||
| − | $Mittelnote$ | + | $\rm Mittelnote \ = \ $ { 3 3% } |
| Zeile 72: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig sind <u>die Lösungsvorschläge 1 und 3</u>: | |
| + | *Nach dem zentralen Grenzwertsatz erhält man für die Summe vieler unabhängiger Größen eine Gaußverteilung. | ||
| + | *Im Umkehrschluss ergibt sich bei nur wenigen und dazu noch abhängigen Aufgaben keine Gaußverteilung. | ||
| + | *Eine einzige Ja/Nein-Frage führt zu einer Zweipunktverteilung $(0$ Punkte oder Maximalpunktzahl$)$. | ||
| + | *Auch bei Einhaltung dieser Gebote wird man bei sehr wenigen Teilnehmern nicht mit einer Gaußverteilung rechnen können. | ||
| + | |||
| + | |||
| − | + | ||
| + | '''(2)''' Man bekommt eine „1.0” mit $82$ Punkten oder mehr. | ||
| + | *Deshalb gilt mit dem Mittelwert $m_z = 60$ und der Streuung $\sigma_z = 10$: | ||
:$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | :$$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) | ||
\hspace{0.15cm}{=\rm 0.0139}.$$ | \hspace{0.15cm}{=\rm 0.0139}.$$ | ||
| + | *Bei tausend Teilnehmern folgt daraus $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$. | ||
| + | |||
| − | |||
| − | + | '''(3)''' Mit weniger als $46$ Punkten hat man die Prüfung nicht bestanden: | |
:$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | :$$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$ | ||
| + | *Also müssen wohl <u>81 Studenten nochmals antreten</u>. | ||
| + | |||
| − | |||
| − | + | '''(4)''' Die Punktedifferenz $82 - 46 = 36$ muss auf neun Notenstufen $(1.3$, ... , $4.0)$ aufgeteilt werden. | |
| + | *Jedes Intervall umfasst somit $4$ Punkte. | ||
| + | *Beispielsweise erhält man die Note „3.0”, wenn man $58$ bis $62$ Punkte erreicht. | ||
| + | *Die Wahrscheinlichkeit, dass die Punktzahl in diesem Bereich liegt, ergibt sich zu | ||
:$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | :$$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$ | ||
| + | *Unter Ausnutzung der Symmetrie erhält man: | ||
| + | :$$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm Teilnehmer)}.$$ | ||
| − | : | + | Anmerkungen: |
| − | + | *$z$ ist als kontinuierliche Zufallsgröße aufzufassen. Deshalb ist die Punktzahl $62$ gleichzeitig die obere Grenze für den „3.0”–Bereich als auch die untere Grenze für die Note „2.7”. | |
| + | *Wäre $z$ nur ganzzahlig, so müsste $62$ je nach Stimmung des Korrektors entweder der Note „2.7” oder der Note „3.0” zugeordnet werden. Natürlich müsste das bei allen Prüflingen in gleicher Weise gemacht werden. | ||
| − | |||
| − | + | ||
| + | '''(5)''' Analog zur Musterlösung der Teilaufgabe '''(4)''' gilt für die Note „2.7”: | ||
:$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | :$$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$ | ||
| − | + | *Aus Symmetriegründen erhält man für die Note „3.3” den gleichen Wert: | |
:$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | :$$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$ | ||
| − | + | *Also erhalten <u>je 146 Teilnehmer die Note „2.7” bzw. „3.3”</u>. | |
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Mit der hier getroffenen Punkte–Noten–Zuordnung sind nicht nur die Punkte um $m_z = 60$ symmetrisch verteilt, sondern auch die Noten um „3.0“. Es gibt | ||
| + | *genau so viele „2.7“ wie „3.3“ $($um $±0.3$ von $3.0$ entfernt$)$, | ||
| + | *genau so viele „2.3“ wie „3.7“ $(3.0 ±0.7)$, und | ||
| + | *genau so viele „1.0“ wie „5.0“. | ||
| + | |||
| − | + | Deshalb ergibt sich die $\rm Mittelnote \hspace{0.15cm}\underline{ 3.0}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 1. Februar 2022, 16:15 Uhr
An einer Prüfung an der TU München haben $1000$ Studentinnen und Studenten teilgenommen. Ab der Note „4.0” gilt die Prüfung als bestanden. Die Prüfungsordnung sieht folgende Noten vor:
- $$1.0, \ 1.3, \ 1.7, \ 2.0, \ 2.3, \ 2.7, \ 3.0, \ 3.3, \ 3.7, \ 4.0, \ 4.3, \ 4.7, \ 5.0.$$
Weiter ist bei der Aufgabe zu berücksichtigen:
- Die maximal erreichbare Punktzahl beträgt $100$. Der beste Student erreichte $88$ Punkte.
- Aufgrund der relativ großen Teilnehmerzahl ergibt sich für die erreichte Punktzahl – dies sei die Zufallsgröße $z$ – mit guter Näherung eine Gaußverteilung mit Mittelwert $m_z = 60$ und Streuung (Standardabweichung) $\sigma_z = 10$.
- Bei der Korrektur wurden nicht nur ganze Punktzahlen vergeben, sondern auch (beliebige) Zwischenwerte, so dass man die Zufallsgröße $z$ mit guter Näherung als „kontinuierlich” auffassen kann.
Für die Bewertung werden als Richtlinien vorgegeben:
- Auch mit sechs Punkten weniger als der Beste $($also ab $82$ Punkten$)$ soll man „1.0” bekommen.
- Hat man $46\%$ der Gesamtpunktzahl erreicht, so hat man die Prüfung bestanden.
- Die Punkte/Noten-Zuordnung soll linear erfolgen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Gaußverteilte Zufallsgrößen.
- Gerade im Schulbereich wird die „Gaußverteilung” oft als „Normalverteilung” bezeichnet. Dies ist nicht ganz korrekt:
- Eine normalverteilte Zufallsgröße $z$ hat zwar eine Gaußsche WDF und VTF, jedoch stets mit Mittelwert $m_z = 0$ und Streuung $\sigma_z = 1$.
Fragebogen
Musterlösung
- Nach dem zentralen Grenzwertsatz erhält man für die Summe vieler unabhängiger Größen eine Gaußverteilung.
- Im Umkehrschluss ergibt sich bei nur wenigen und dazu noch abhängigen Aufgaben keine Gaußverteilung.
- Eine einzige Ja/Nein-Frage führt zu einer Zweipunktverteilung $(0$ Punkte oder Maximalpunktzahl$)$.
- Auch bei Einhaltung dieser Gebote wird man bei sehr wenigen Teilnehmern nicht mit einer Gaußverteilung rechnen können.
(2) Man bekommt eine „1.0” mit $82$ Punkten oder mehr.
- Deshalb gilt mit dem Mittelwert $m_z = 60$ und der Streuung $\sigma_z = 10$:
- $$\rm Pr(\it z\ge \rm 82)=\rm Q\Bigg(\frac{\rm 82-60}{\rm 10}\Bigg)=\rm Q(\rm 2.2) \hspace{0.15cm}{=\rm 0.0139}.$$
- Bei tausend Teilnehmern folgt daraus $N_\text{1.0}\hspace{0.15cm}\underline{= 14}$.
(3) Mit weniger als $46$ Punkten hat man die Prüfung nicht bestanden:
- $$\rm Pr(\it z<\rm 46)=\rm Pr(\it z \le \rm 46)=\rm \phi\Bigg(\frac{\rm 46-60}{\rm 10}\Bigg)=\rm \phi(\rm -1.4)=\rm Q(\rm 1.4)=\rm 0.0807.$$
- Also müssen wohl 81 Studenten nochmals antreten.
(4) Die Punktedifferenz $82 - 46 = 36$ muss auf neun Notenstufen $(1.3$, ... , $4.0)$ aufgeteilt werden.
- Jedes Intervall umfasst somit $4$ Punkte.
- Beispielsweise erhält man die Note „3.0”, wenn man $58$ bis $62$ Punkte erreicht.
- Die Wahrscheinlichkeit, dass die Punktzahl in diesem Bereich liegt, ergibt sich zu
- $$\rm Pr(\rm 58 <\it z<\rm 62)=\rm \phi\Bigg(\frac{\rm 62-60}{\rm 10}\Bigg)-\rm \phi\Bigg(\frac{\rm 58-60}{\rm 10}\Bigg).$$
- Unter Ausnutzung der Symmetrie erhält man:
- $$\rm Pr(\rm 58 <\it z<\rm 62) = \rm \phi(\rm 0.2)-\rm \phi(\rm -0.2) = \rm 0.5792-\rm 0.4207=0.1587\hspace{0.2cm}\hspace{0.15cm}\underline{(159 \hspace{0.1cm}\rm Teilnehmer)}.$$
Anmerkungen:
- $z$ ist als kontinuierliche Zufallsgröße aufzufassen. Deshalb ist die Punktzahl $62$ gleichzeitig die obere Grenze für den „3.0”–Bereich als auch die untere Grenze für die Note „2.7”.
- Wäre $z$ nur ganzzahlig, so müsste $62$ je nach Stimmung des Korrektors entweder der Note „2.7” oder der Note „3.0” zugeordnet werden. Natürlich müsste das bei allen Prüflingen in gleicher Weise gemacht werden.
(5) Analog zur Musterlösung der Teilaufgabe (4) gilt für die Note „2.7”:
- $$\rm Pr(\rm 62 <\it z<\rm 66)=\rm \phi(\rm 0.6)-\rm \phi(\rm 0.2)=\rm 0.7257-\rm 0.5792=0.1465.$$
- Aus Symmetriegründen erhält man für die Note „3.3” den gleichen Wert:
- $$\rm Pr(\rm 54 <\it z<\rm 58)=\rm \phi(-\rm 0.2)-\rm \phi(-\rm 0.6)= \rm Q(\rm 0.2)-\rm Q(\rm 0.6)=\rm 0.1465.$$
- Also erhalten je 146 Teilnehmer die Note „2.7” bzw. „3.3”.
(6) Mit der hier getroffenen Punkte–Noten–Zuordnung sind nicht nur die Punkte um $m_z = 60$ symmetrisch verteilt, sondern auch die Noten um „3.0“. Es gibt
- genau so viele „2.7“ wie „3.3“ $($um $±0.3$ von $3.0$ entfernt$)$,
- genau so viele „2.3“ wie „3.7“ $(3.0 ±0.7)$, und
- genau so viele „1.0“ wie „5.0“.
Deshalb ergibt sich die $\rm Mittelnote \hspace{0.15cm}\underline{ 3.0}$.