Aufgaben:Aufgabe 3.11: Auslöschungskanal: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2791__Inf_A_3_10.png|right|]] | + | [[Datei:P_ID2791__Inf_A_3_10.png|right|frame|Auslöschungskanal mit vier Eingängen und fünf Ausgängen]] |
Betrachtet wird ein Auslöschungskanal mit | Betrachtet wird ein Auslöschungskanal mit | ||
| − | + | * den $M$ Eingängen $x ∈ X = \{1,\ 2, \ \text{...} \ ,\ M\}$, und | |
| − | + | * den $M + 1$ Ausgängen $y ∈ Y = \{1,\ 2,\ \ \text{...} \ ,\ M,\ \text{E}\}.$ | |
| − | |||
| − | Die Übergangswahrscheinlichkeiten sind für $1 ≤ μ ≤ M$ wie folgt gegeben: | + | Die Grafik zeigt das Modell für den Sonderfall $M = 4$. Das Sinkensymbol $y = \text{E}$ berücksichtigt eine „Auslöschung” (englisch: "Erasure") für den Fall, dass der Empfänger keine hinreichend gesicherte Entscheidung treffen kann. |
| − | $${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) | + | |
| − | $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) | + | Die Übergangswahrscheinlichkeiten sind für $1 ≤ μ ≤ M$ wie folgt gegeben: |
| − | Gesucht | + | :$${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = 1-\lambda \hspace{0.05cm},$$ |
| − | + | :$${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = \lambda \hspace{0.05cm}.$$ | |
| − | + | Gesucht werden: | |
| − | '' | + | * die Kapazität $C_{M\rm –EC}$ dieses "M–ary Erasure Channels", |
| + | * die Kapazität $C_{\rm BEC}$ des [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|Binary Erasure Channels]] $\rm (BEC)$ als Sonderfall des obigen Modells. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Informationstheoretisches_Modell_der_Digitalsignal.C3.BCbertragung|Informationstheoretisches Modell der Digitalsignalübertragung]]. | ||
| + | *Im obigen Schaubild sind Auslöschungen $($mit Wahrscheinlichkeit $λ)$ blau gezeichnet. | ||
| + | * „Richtige Übertragungswege” $($also von $X = μ$ nach $Y = μ)$ sind rot dargestellt $(1 ≤ μ ≤ M)$. | ||
| + | |||
| + | |||
| Zeile 22: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { Welches $P_X(X)$ ist zur Kanalkapazitätsberechnung allgemein anzusetzen? | + | { Welches $P_X(X)$ ist zur Kanalkapazitätsberechnung allgemein anzusetzen? |
|type="[]"} | |type="[]"} | ||
| − | - $P_X(X) = (0.5, 0.5)$ | + | - $P_X(X) = (0.5, \ 0.5),$ |
| − | + $P_X(X) = (1/M, 1/M, ... , 1/M)$ | + | + $P_X(X) = (1/M,\ 1/M, \ \text{...} \ ,\ 1/M),$ |
| − | - $P_X(X) = (0.1, 0.2, 0.3, 0.4)$ | + | - $P_X(X) = (0.1,\ 0.2,\ 0.3,\ 0.4).$ |
| − | {Wie viele Wahrscheinlichkeiten $p_{μκ} = Pr[(X = μ) ∩ (Y = κ)]$ sind | + | {Wie viele Wahrscheinlichkeiten $p_{μκ} = {\rm Pr}\big[(X = μ) ∩ (Y = κ)\big]$ sind ungleich Null? |
| − | |type=" | + | |type="()"} |
| − | - Genau $M · (M + 1)$ | + | - Genau $M · (M + 1)$, |
| − | - Genau $M$ | + | - Genau $M$, |
| − | + Genau $2 · M$ | + | + Genau $2 · M$. |
| − | {Wie groß ist die Sinkenentropie allgemein und für $M = 4$ und $λ = 0.2$? | + | {Wie groß ist die Sinkenentropie allgemein und für $M = 4$ und $λ = 0.2$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H(Y) \ = \ $ { 2.322 3% } $\ \rm bit$ |
| − | {Berechnen Sie die Irrelevanz. Welcher Wert ergibt sich für $M = 4 | + | {Berechnen Sie die Irrelevanz. Welcher Wert ergibt sich für $M = 4$ und $λ = 0.2$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H(Y|X) \ = \ $ { 0.722 3% } $\ \rm bit$ |
| − | {Wie groß ist die Kanalkapazität in Abhängigkeit von $M$? | + | {Wie groß ist die Kanalkapazität $C$ in Abhängigkeit von $M$? |
|type="{}"} | |type="{}"} | ||
| − | $M = 4: C$ | + | $M = 4\text{:} \hspace{0.5cm} C\ = \ $ { 1.6 3% } $\ \rm bit$ |
| − | $M = 2: C$ | + | $M = 2\text{:} \hspace{0.5cm} C\ = \ $ { 0.8 3% } $\ \rm bit$ |
{Wie lautet die Kanalkapazität des BEC–Kanals in kompakter Form? | {Wie lautet die Kanalkapazität des BEC–Kanals in kompakter Form? | ||
| − | |type=" | + | |type="()"} |
| − | + $C_{BEC} = 1 | + | + $C_{\rm BEC} = 1 - λ,$ |
| − | - $C_{BEC} = 1 | + | - $C_{\rm BEC} = 1 - H_{\rm bin}(λ).$ |
| Zeile 60: | Zeile 75: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2:</u> |
| − | $$ P_X(X) = P_X\big ( \hspace{0.03cm}X\hspace{-0.03cm}=1\hspace{0.03cm}, \hspace{0. | + | * Aufgrund der Symmetrie der Übergangswahrscheinlichkeiten $P_{Y|X}(Y|X)$ ist offensichtlich, dass eine Gleichverteilung zur maximalen Transinformation $I(X; Y)$ und damit zur Kanalkapazität $C$ führen wird: |
| − | + | :$$ P_X(X) = P_X\big ( \hspace{0.03cm}X\hspace{-0.03cm}=1\hspace{0.03cm}, \hspace{0.08cm} X\hspace{-0.03cm}=2\hspace{0.03cm},\hspace{0.08cm}\text{...}\hspace{0.08cm}, X\hspace{-0.03cm}=M\hspace{0.03cm}\big ) = \big [\hspace{0.03cm}1/M\hspace{0.03cm}, \hspace{0.08cm} 1/M\hspace{0.03cm},\hspace{0.03cm}\text{...}\hspace{0.08cm},\hspace{0.08cm} 1/M\hspace{0.03cm}\big ]\hspace{0.05cm}.$$ | |
| + | *Im Sonderfall $M = 2$ wäre auch $P_X(X) = (0.5, \ 0.5)$ richtig. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Zutreffend ist der <u>Lösungsvorschlag 3</u>, also genau $2M$ Verbindungen. Da: | ||
| + | *Von jedem Quellensymbol $X = μ$ kommt man sowohl zum Sinkensymbol $Y = μ$ als auch zum Erasure $Y = \text{E}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Alle Wahrscheinlichkeiten ${\rm Pr}(Y = 1), \hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.08cm}{\rm Pr}(Y = M)$ sind gleich groß. Damit erhält man für $μ = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.08cm} M$: | ||
| + | :$${\rm Pr}(Y \hspace{-0.05cm} = \mu) = ( 1-\lambda)/M \hspace{0.05cm}.$$ | ||
| + | *Außerdem kommt man von jedem Quellensymbol $X = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm} , X = M$ auch zum Erasure $Y = \text{E}$: | ||
| + | :$${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}) = \lambda \hspace{0.05cm}.$$ | ||
| + | *Die Kontrolle ergibt, dass die Summe aller $M + 1$ Sinkensymbolwahrscheinlichkeiten tatsächlich $1$ ergibt. | ||
| + | *Daraus folgt für die Sinkenentropie: | ||
| + | :$$H(Y) = M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{M}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\lambda} \hspace{0.05cm}.$$ | ||
| + | *Zusammengefasst ergibt dies mit der binären Entropiefunktion: | ||
| + | :$$H(Y) = (1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm}+\hspace{0.15cm} H_{\rm bin} (\lambda ) \hspace{0.05cm}$$ | ||
| + | :und mit $M = 4$ sowie $ λ = 0.2$: | ||
| + | :$$H(Y) = 1.6 \,{\rm bit} + H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=2.322\,{\rm bit}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Die $2M$ Verbundwahrscheinlichkeiten | ||
| + | :$${\rm Pr} \big[(X = μ) ∩ (Y = κ)\big] ≠ 0$$ | ||
| + | :und die bedingten Wahrscheinlichkeiten | ||
| + | :$$pκ|μ = {\rm Pr}(Y = κ|X = μ)$$ | ||
| + | :zeigen folgende Eigenschaften: | ||
| + | # Die Kombination $p_{μκ} = (1 – λ)/M$ und $p_{κ|μ} = 1 – λ$ kommt $M$ mal vor. | ||
| + | # Die Kombination $p_{μκ} = λ/M$ und $p_{κ|μ} = λ$ kommt ebenfalls $M$ mal vor. | ||
| + | |||
| + | |||
| + | Daraus folgt: | ||
| + | :$$ H(Y \hspace{-0.15cm}\mid \hspace{-0.15cm} X) \hspace{-0.01cm} =\hspace{-0.01cm} M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm}M \cdot \frac{ \lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = H_{\rm bin} (\lambda)\hspace{0.05cm}.$$ | ||
| + | *Das Ergebnis ist unabhängig von $M$. Mit $λ = 0.2$ erhält man: | ||
| + | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=0.722\,{\rm bit}} \hspace{0.05cm}.$$ | ||
| + | |||
| − | |||
| − | ''' | + | '''(5)''' Die Kanalkapazität $C$ ist gleich der maximalen Transinformation $I(X; Y)$, wobei die Maximierung hinsichtlich $P_X(X)$ bereits durch den symmetrischen Ansatz berücksichtigt wurde: |
| − | $${ | + | :$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M + H_{\rm bin} (\lambda) - H_{\rm bin} (\lambda) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.05cm}$$ |
| − | + | :$$\Rightarrow \hspace{0.3cm} M = 4\text{:} \hspace{0.3cm} \underline {C=1.6\,\,{\rm bit}} \hspace{0.05cm}, \hspace{0.8cm} | |
| − | + | M = 2\text{:} \hspace{0.3cm} \underline {C=0.8\,\,{\rm bit}} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| − | $$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' Der "Binary Erasure Channel" $\rm (BEC)$ ist ein Sonderfall des hier betrachteten allgemeinen Modells mit $M = 2$: |
| − | $$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}$$ | + | :$$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$ |
| − | Richtig ist somit der | + | *Richtig ist somit der <u>Lösungsvorschlag 1</u>. |
| + | *Der zweite Lösungsvorschlag gilt dagegen für den "Binary Symmetric Channel" $\rm (BSC)$ mit der Verfälschungswahrscheinlichkeit $λ$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 22. September 2021, 12:31 Uhr
Betrachtet wird ein Auslöschungskanal mit
- den $M$ Eingängen $x ∈ X = \{1,\ 2, \ \text{...} \ ,\ M\}$, und
- den $M + 1$ Ausgängen $y ∈ Y = \{1,\ 2,\ \ \text{...} \ ,\ M,\ \text{E}\}.$
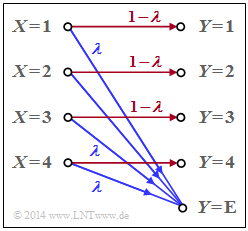
Die Grafik zeigt das Modell für den Sonderfall $M = 4$. Das Sinkensymbol $y = \text{E}$ berücksichtigt eine „Auslöschung” (englisch: "Erasure") für den Fall, dass der Empfänger keine hinreichend gesicherte Entscheidung treffen kann.
Die Übergangswahrscheinlichkeiten sind für $1 ≤ μ ≤ M$ wie folgt gegeben:
- $${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = 1-\lambda \hspace{0.05cm},$$
- $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = \lambda \hspace{0.05cm}.$$
Gesucht werden:
- die Kapazität $C_{M\rm –EC}$ dieses "M–ary Erasure Channels",
- die Kapazität $C_{\rm BEC}$ des Binary Erasure Channels $\rm (BEC)$ als Sonderfall des obigen Modells.
Hinweise:
- Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
- Bezug genommen wird insbesondere auf die Seite Informationstheoretisches Modell der Digitalsignalübertragung.
- Im obigen Schaubild sind Auslöschungen $($mit Wahrscheinlichkeit $λ)$ blau gezeichnet.
- „Richtige Übertragungswege” $($also von $X = μ$ nach $Y = μ)$ sind rot dargestellt $(1 ≤ μ ≤ M)$.
Fragebogen
Musterlösung
- Aufgrund der Symmetrie der Übergangswahrscheinlichkeiten $P_{Y|X}(Y|X)$ ist offensichtlich, dass eine Gleichverteilung zur maximalen Transinformation $I(X; Y)$ und damit zur Kanalkapazität $C$ führen wird:
- $$ P_X(X) = P_X\big ( \hspace{0.03cm}X\hspace{-0.03cm}=1\hspace{0.03cm}, \hspace{0.08cm} X\hspace{-0.03cm}=2\hspace{0.03cm},\hspace{0.08cm}\text{...}\hspace{0.08cm}, X\hspace{-0.03cm}=M\hspace{0.03cm}\big ) = \big [\hspace{0.03cm}1/M\hspace{0.03cm}, \hspace{0.08cm} 1/M\hspace{0.03cm},\hspace{0.03cm}\text{...}\hspace{0.08cm},\hspace{0.08cm} 1/M\hspace{0.03cm}\big ]\hspace{0.05cm}.$$
- Im Sonderfall $M = 2$ wäre auch $P_X(X) = (0.5, \ 0.5)$ richtig.
(2) Zutreffend ist der Lösungsvorschlag 3, also genau $2M$ Verbindungen. Da:
- Von jedem Quellensymbol $X = μ$ kommt man sowohl zum Sinkensymbol $Y = μ$ als auch zum Erasure $Y = \text{E}$.
(3) Alle Wahrscheinlichkeiten ${\rm Pr}(Y = 1), \hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.08cm}{\rm Pr}(Y = M)$ sind gleich groß. Damit erhält man für $μ = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.08cm} M$:
- $${\rm Pr}(Y \hspace{-0.05cm} = \mu) = ( 1-\lambda)/M \hspace{0.05cm}.$$
- Außerdem kommt man von jedem Quellensymbol $X = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm} , X = M$ auch zum Erasure $Y = \text{E}$:
- $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}) = \lambda \hspace{0.05cm}.$$
- Die Kontrolle ergibt, dass die Summe aller $M + 1$ Sinkensymbolwahrscheinlichkeiten tatsächlich $1$ ergibt.
- Daraus folgt für die Sinkenentropie:
- $$H(Y) = M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{M}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\lambda} \hspace{0.05cm}.$$
- Zusammengefasst ergibt dies mit der binären Entropiefunktion:
- $$H(Y) = (1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm}+\hspace{0.15cm} H_{\rm bin} (\lambda ) \hspace{0.05cm}$$
- und mit $M = 4$ sowie $ λ = 0.2$:
- $$H(Y) = 1.6 \,{\rm bit} + H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=2.322\,{\rm bit}} \hspace{0.05cm}.$$
(4) Die $2M$ Verbundwahrscheinlichkeiten
- $${\rm Pr} \big[(X = μ) ∩ (Y = κ)\big] ≠ 0$$
- und die bedingten Wahrscheinlichkeiten
- $$pκ|μ = {\rm Pr}(Y = κ|X = μ)$$
- zeigen folgende Eigenschaften:
- Die Kombination $p_{μκ} = (1 – λ)/M$ und $p_{κ|μ} = 1 – λ$ kommt $M$ mal vor.
- Die Kombination $p_{μκ} = λ/M$ und $p_{κ|μ} = λ$ kommt ebenfalls $M$ mal vor.
Daraus folgt:
- $$ H(Y \hspace{-0.15cm}\mid \hspace{-0.15cm} X) \hspace{-0.01cm} =\hspace{-0.01cm} M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm}M \cdot \frac{ \lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = H_{\rm bin} (\lambda)\hspace{0.05cm}.$$
- Das Ergebnis ist unabhängig von $M$. Mit $λ = 0.2$ erhält man:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=0.722\,{\rm bit}} \hspace{0.05cm}.$$
(5) Die Kanalkapazität $C$ ist gleich der maximalen Transinformation $I(X; Y)$, wobei die Maximierung hinsichtlich $P_X(X)$ bereits durch den symmetrischen Ansatz berücksichtigt wurde:
- $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M + H_{\rm bin} (\lambda) - H_{\rm bin} (\lambda) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} M = 4\text{:} \hspace{0.3cm} \underline {C=1.6\,\,{\rm bit}} \hspace{0.05cm}, \hspace{0.8cm} M = 2\text{:} \hspace{0.3cm} \underline {C=0.8\,\,{\rm bit}} \hspace{0.05cm}.$$
(6) Der "Binary Erasure Channel" $\rm (BEC)$ ist ein Sonderfall des hier betrachteten allgemeinen Modells mit $M = 2$:
- $$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$
- Richtig ist somit der Lösungsvorschlag 1.
- Der zweite Lösungsvorschlag gilt dagegen für den "Binary Symmetric Channel" $\rm (BSC)$ mit der Verfälschungswahrscheinlichkeit $λ$.