Aufgaben:Aufgabe 2.4Z: Nochmals LZW-Codierung und -Decodierung: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2437__Inf_Z_2_4.png|right|Momentaufnahmen | + | [[Datei:P_ID2437__Inf_Z_2_4.png|right|frame|Momentaufnahmen <br>der LZW–Wörterbücher]] |
| − | Die | + | Die Grafik zeigt Momentaufnahmen des Wörterbuchs, das während der <u>LZW–Codierung</u> der Eingangssymbolfolge entsteht: |
| + | *Die obere Grafik gilt für Eingangssymbolfolge <b>ABABABBAA</b>. | ||
| + | *Das untere Wörterbuch entsteht bei der LZW–Codierung der Sequenz <b>ABABABABA</b>. | ||
| − | |||
| − | + | In beiden Fällen wird vorausgesetzt, dass auch zu späteren Zeitpunkten keine anderen Zeichen als <b>A</b> und <b>B</b> vorkommen können. | |
| − | Bei der LZW–Decodierung | + | Bei der <u>LZW–Decodierung</u> entstehen gleiche Wörterbücher, doch erfolgen dann die Wörterbucheinträge erst einen Schritt später. In der Teilaufgabe '''(3)''' wird gefragt, für welchen Codierschritt bzw. Decodierschritt die beiden dargestellten Momentaufnahmen gültig sind. |
| − | Wird tatsächlich ein Wörterbucheintrag mit dem gewünschten Index | + | |
| − | * Wird bei der Codierung beim Schritt | + | Bei der <u>LZW–Codierung</u> wird zu jedem Codierschritt $i$ ein Index $I$ ausgewählt und (binär) übertragen. Das Zeichenpaar <b>AB</b> wird bei den beiden Wörterbüchern durch den Index $I = 2$ dargestellt. Wir betrachten hier den Index $I$ als Dezimalzahl und lassen bei dieser Aufgabe die Binärdarstellung außer Betracht. |
| − | * Bei binärer Eingangsfolge (alle Zeichen seien <b>A</b> oder <b>B</b>) ist bei der LZW–Decodierung genau immer dann eine Sonderregelung anzuwenden, wenn im Codierschritt | + | |
| + | |||
| + | Bei der <u>LZW–Decodierung</u> wird in gleicher Weise mit Hilfe des Wörterbuchs aus jedem Index $I$ ein Zeichen bzw. eine Zeichenfolge generiert, zum Beispiel führt $I = 1$ zum Zeichen <b>B</b> und $I = 2$ zum Zeichenpaar <b>AB</b>. | ||
| + | |||
| + | Wird tatsächlich ein Wörterbucheintrag mit dem gewünschten Index $I$ gefunden, so läuft die Decodierung problemlos ab. Dies ist aber nicht immer so: | ||
| + | * Wird bei der Codierung beim Schritt $i$ ein neuer Index $I$ eingetragen und ist dieses $I$ gleichzeitig das Codierergebnis des Schrittes, so ist dieser Index beim Decodierschritt $i$ im Wörterbuch noch nicht belegt. Der Grund hierfür ist, dass beim Decoder die Einträge um einen Schritt später erfolgen als beim Coder. | ||
| + | * Bei binärer Eingangsfolge $($alle Zeichen seien <b>A</b> oder <b>B</b>$)$ ist bei der LZW–Decodierung genau immer dann eine Sonderregelung anzuwenden, wenn im Codierschritt $i$ der Eintrag mit dem Index $I = i$ vorgenommen wurde. | ||
Diese Sonderregelung soll an einem Beispiel veranschaulicht werden: | Diese Sonderregelung soll an einem Beispiel veranschaulicht werden: | ||
| − | * Zum Schritt | + | * Zum Schritt $i$ gibt es keinen zum Index $I$ passenden Eintrag im Decoder–Wörterbuch. |
| − | * Wir nehmen an, dass | + | * Wir nehmen an, dass beim vorherigen Schritt $(i- 1)$ das Decodierergebnis <b>ABBABA</b> war. |
| − | * Dann ergänzt man diese Zeichenfolge um das erste Zeichen der Folge. Hier: <b>ABBABAA</b>. | + | * Dann ergänzt man diese Zeichenfolge um das erste Zeichen der Folge. Hier: <b>ABBABAA</b>. |
| − | * Anschließend trägt man die Sequenz <b>ABBABAA</b> in das Wörterbuch unter dem Index | + | * Anschließend trägt man die Sequenz <b>ABBABAA</b> in das Wörterbuch unter dem Index $I$ ein. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch|Komprimierung nach Lempel, Ziv und Welch]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch|Komprimierung nach Lempel, Ziv und Welch]]. |
| − | *Insbesondere wird Bezug genommen auf die Seiten [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch# | + | *Insbesondere wird Bezug genommen auf die Seiten |
| − | + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#LZ77_.E2.80.93_die_Grundform_der_Lempel.E2.80.93Ziv.E2.80.93Algorithmen|LZ77 – die Grundform der Lempel-Ziv-Algorithmen]], | |
| − | *Beachten Sie bei der Lösung dieser Aufgabe, dass beim LZW–Algorithmus nicht von einem leeren Wörterbuch ausgegangen wird. Vielmehr beinhalten die Indizes | + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Lempel.E2.80.93Ziv.E2.80.93Codierung_mit_variabler_Indexbitl.C3.A4nge|Lempel-Ziv-Codierung mit variabler Indexbitlänge]], |
| + | :: [[Informationstheorie/Komprimierung_nach_Lempel,_Ziv_und_Welch#Decodierung_des_LZW.E2.80.93Algorithmus|Decodierung des LZW-Agorithmus]]. | ||
| + | *Beachten Sie zudem bei der Lösung dieser Aufgabe, dass beim LZW–Algorithmus nicht von einem leeren Wörterbuch ausgegangen wird. | ||
| + | *Vielmehr beinhalten die Indizes $I = 0$ bis $I = M- 1$ alle $M$ zulässigen Zeichen des Alphabets. | ||
| Zeile 34: | Zeile 50: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Codieren Sie die Eingangsfolge <b>ABABABBAA</b> | + | {Codieren Sie die Eingangsfolge <b>ABABABBAA</b> entsprechend der <u>oberen Grafik</u>. Welche Indizes $I_i$ ergeben sich zu den Schritten $i=1$, ... , $i=5$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I_1 \ = \ $ { 0. } |
| − | $ | + | $I_2 \ = \ $ { 1 } |
| − | $ | + | $I_3 \ = \ $ { 2 } |
| − | $ | + | $I_4 \ = \ $ { 2 } |
| − | $ | + | $I_5 \ = \ $ { 3 } |
| − | {Codieren Sie nun die Eingangsfolge <b>ABABABABA</b>. Geben Sie die Indizes | + | {Codieren Sie nun die Eingangsfolge <b>ABABABABA</b> entsprechend der <u>unteren Grafik</u>. Geben Sie die Indizes $I_i$ zu den Schritten $i=4$ und $i=5$ an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I_4 \ = \ $ { 4 } |
| − | $ | + | $I_5 \ = \ $ { 3 } |
| − | {Für welchen Schritt | + | {Für welchen Schritt $i$ gilt die Momentaufnahme des auf der Angabenseite dargestellten Wörterbuchs bezüglich |
|type="{}"} | |type="{}"} | ||
| − | $\text{Codierung:} \ \ i \ = $ { 4 } | + | $\text{Codierung:} \ \ i \ = \ $ { 4 } |
| − | $\text{Decodierung:} \ \ i \ = $ { 5 } | + | $\text{Decodierung:} \ \ i \ = \ $ { 5 } |
{Wann muss man auf die Decodier–Sonderfallregelung zurückgreifen? | {Wann muss man auf die Decodier–Sonderfallregelung zurückgreifen? | ||
|type="[]"} | |type="[]"} | ||
| − | - Bei der Decodierung von <b>ABABABBAA</b> im Schritt | + | - Bei der Decodierung von <b>ABABABBAA</b> im Schritt $i = 4$. |
| − | + Bei der Decodierung von <b>ABABABABA</b> im Schritt | + | + Bei der Decodierung von <b>ABABABABA</b> im Schritt $i = 4$. |
| − | - Bei der Decodierung von <b>ABABABABA</b> im Schritt | + | - Bei der Decodierung von <b>ABABABABA</b> im Schritt $i = 5$. |
| Zeile 68: | Zeile 84: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Wir bezeichnen mit $W(I)$ ein Feld (Array), welches das Wörterbuch beschreibt und dessen Elemente Character oder Zeichenfolgen beinhalten. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *Die Codierung von <b>ABABABBAA</b> läuft dann wie folgt ab: | |
| + | :: $i = 1$: <b>A</b> → $\underline{I=0}$, $W(I = 2) =$ <b>AB</b>, | ||
| + | :: $i = 2$: <b>B</b> → $\underline{I=1}$, $W(I = 3) =$ <b>BA</b>, | ||
| + | :: $i = 3$: <b>AB</b> → $\underline{I=2}$, $W(I = 4) =$ <b>ABA</b>, | ||
| + | :: $i = 4$: <b>AB</b> → $\underline{I=2}$, $W(I = 5) =$ <b>ABB</b>, | ||
| + | :: $i = 5$: <b>BA</b> → $\underline{I=3}$, $W(I = 6) =$ <b>BAA</b>. | ||
| − | + | *Es ist anzumerken, dass das letzte Zeichen $($<b>A</b>$)$ des Eingabestrings <b>ABABABBAA</b> zum Zeitpunkt $i = 5$ zwar bereits beim Wörterbucheintrag berücksichtigt ist, aber noch nicht codiert wurde. | |
| − | |||
| − | |||
| − | + | '''(2)''' Für die Schritte $i = 1$ bis $i = 3$ ändert sich nichts gegenüber der Teilaufgabe '''(1)'''. | |
| + | *Danach gilt: | ||
| + | :: $i = 4$: <b>ABA</b> → $\underline{I=4}$, $W(I = 5) =$ <b>ABAB</b>, | ||
| + | :: $i = 5$: <b>BA</b> → $\underline{I=3}$, Codierung abgeschlossen, kein neuer Wörterbucheintrag möglich. | ||
| − | |||
| − | |||
| − | :< | + | '''(3)''' Der Vergleich mit obigen Ergebnissen zeigt: |
| + | *Das Wörterbuch des <u>Coders</u> weist genau nach $\underline{i=4}$ Codierschritten die gezeigten Einträge auf. | ||
| + | *Beim <u>Decoder</u> ergibt sich demgegenüber eine Zeitverzögerung um einen Schritt: $\underline{i=5}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | |
| + | *Die Sonderfallregelung der Decodierung ist (im vorliegenden Beispiel) dann notwendig, wenn im Codierschritt $i$ der Index $I =i$ ausgegeben wird. | ||
| + | *Bei der Decodierung findet er dann die erforderliche Zuordnung „Index → Zeichenfolge” nicht, da das generierte Wörterbuch zum Zeitpunkt $i$ nur Einträge mit Indizes $I < i$ enthält. | ||
| + | *Für die Folge <b>ABABABBAA</b> gilt entsprechend der Teilaufgabe '''(1)''' stets $I < i$. | ||
| + | *Dagegen ergäbe sich für die Folge <b>ABABABABA</b> folgende Indizes: | ||
| + | :$$i = 1\hspace{-0.15cm}: \hspace{0.15cm} I = 0\hspace{0.05cm}, | ||
| + | \hspace{0.5cm}i = 2\hspace{-0.15cm}: \hspace{0.15cm}I = 1\hspace{0.05cm}, | ||
| + | \hspace{0.5cm}i = 3\hspace{-0.15cm}: \hspace{0.15cm}I = 2\hspace{0.05cm}, | ||
| + | \hspace{0.5cm}\underline{i = 4\hspace{-0.15cm}: \hspace{0.15cm}I = 4}\hspace{0.05cm}, | ||
| + | \hspace{0.5cm}i = 5\hspace{-0.15cm}: \hspace{0.15cm}I = 3\hspace{0.05cm}. $$ | ||
| − | + | Hier noch zusammenfassend die gesamte Decodierung von <b>ABABABABA</b>: | |
| − | + | *Die Vorbelegung des Wörterbuchs beinhaltet $(I=0$: <b>A</b>$)$ und $(I=1$: <b>B</b>$)$. | |
| − | : | + | *Dann gilt mit dem Wörterbuch–Array $W(I)$: |
| + | :: $i = 1$: Decodierung $I=0$ → <b>A</b>, | ||
| + | :: $i = 2$: Decodierung $I=1$ → <b>B</b>, $W(I = 2) =$ <b>AB</b>, | ||
| + | :: $i = 3$: Decodierung $I=2$ → <b>AB</b>, $W(I = 3) =$ <b>BA</b>, | ||
| + | :: $i = 4$: Ein Eintrag mit dem Index $I = 4$ ist nicht vorhanden ⇒ '''Sonderfallregelung''': <br> Man nimmt das letzte Decodierergebnis $($hier <b>AB</b>$)$ und fügt das erste Zeichen dieser Sequenz hinten an ⇒ <b>ABA</b>. <br> Danach wird <b>ABA</b> im Wörterbuch unter dem Index $I = 4$ abgelegt. | ||
| + | :: $i = 5$: Decodierung $I=3$ → <b>BA</b>. '''Ende der Decoder–Eingangsfolge'''. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 17. Juli 2021, 13:22 Uhr
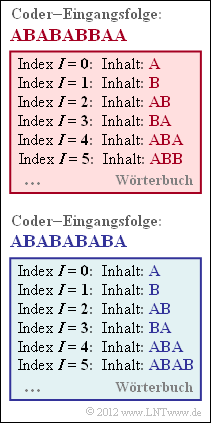
Die Grafik zeigt Momentaufnahmen des Wörterbuchs, das während der LZW–Codierung der Eingangssymbolfolge entsteht:
- Die obere Grafik gilt für Eingangssymbolfolge ABABABBAA.
- Das untere Wörterbuch entsteht bei der LZW–Codierung der Sequenz ABABABABA.
In beiden Fällen wird vorausgesetzt, dass auch zu späteren Zeitpunkten keine anderen Zeichen als A und B vorkommen können.
Bei der LZW–Decodierung entstehen gleiche Wörterbücher, doch erfolgen dann die Wörterbucheinträge erst einen Schritt später. In der Teilaufgabe (3) wird gefragt, für welchen Codierschritt bzw. Decodierschritt die beiden dargestellten Momentaufnahmen gültig sind.
Bei der LZW–Codierung wird zu jedem Codierschritt $i$ ein Index $I$ ausgewählt und (binär) übertragen. Das Zeichenpaar AB wird bei den beiden Wörterbüchern durch den Index $I = 2$ dargestellt. Wir betrachten hier den Index $I$ als Dezimalzahl und lassen bei dieser Aufgabe die Binärdarstellung außer Betracht.
Bei der LZW–Decodierung wird in gleicher Weise mit Hilfe des Wörterbuchs aus jedem Index $I$ ein Zeichen bzw. eine Zeichenfolge generiert, zum Beispiel führt $I = 1$ zum Zeichen B und $I = 2$ zum Zeichenpaar AB.
Wird tatsächlich ein Wörterbucheintrag mit dem gewünschten Index $I$ gefunden, so läuft die Decodierung problemlos ab. Dies ist aber nicht immer so:
- Wird bei der Codierung beim Schritt $i$ ein neuer Index $I$ eingetragen und ist dieses $I$ gleichzeitig das Codierergebnis des Schrittes, so ist dieser Index beim Decodierschritt $i$ im Wörterbuch noch nicht belegt. Der Grund hierfür ist, dass beim Decoder die Einträge um einen Schritt später erfolgen als beim Coder.
- Bei binärer Eingangsfolge $($alle Zeichen seien A oder B$)$ ist bei der LZW–Decodierung genau immer dann eine Sonderregelung anzuwenden, wenn im Codierschritt $i$ der Eintrag mit dem Index $I = i$ vorgenommen wurde.
Diese Sonderregelung soll an einem Beispiel veranschaulicht werden:
- Zum Schritt $i$ gibt es keinen zum Index $I$ passenden Eintrag im Decoder–Wörterbuch.
- Wir nehmen an, dass beim vorherigen Schritt $(i- 1)$ das Decodierergebnis ABBABA war.
- Dann ergänzt man diese Zeichenfolge um das erste Zeichen der Folge. Hier: ABBABAA.
- Anschließend trägt man die Sequenz ABBABAA in das Wörterbuch unter dem Index $I$ ein.
Hinweise:
- Die Aufgabe gehört zum Kapitel Komprimierung nach Lempel, Ziv und Welch.
- Insbesondere wird Bezug genommen auf die Seiten
- Beachten Sie zudem bei der Lösung dieser Aufgabe, dass beim LZW–Algorithmus nicht von einem leeren Wörterbuch ausgegangen wird.
- Vielmehr beinhalten die Indizes $I = 0$ bis $I = M- 1$ alle $M$ zulässigen Zeichen des Alphabets.
Fragebogen
Musterlösung
- Die Codierung von ABABABBAA läuft dann wie folgt ab:
- $i = 1$: A → $\underline{I=0}$, $W(I = 2) =$ AB,
- $i = 2$: B → $\underline{I=1}$, $W(I = 3) =$ BA,
- $i = 3$: AB → $\underline{I=2}$, $W(I = 4) =$ ABA,
- $i = 4$: AB → $\underline{I=2}$, $W(I = 5) =$ ABB,
- $i = 5$: BA → $\underline{I=3}$, $W(I = 6) =$ BAA.
- Es ist anzumerken, dass das letzte Zeichen $($A$)$ des Eingabestrings ABABABBAA zum Zeitpunkt $i = 5$ zwar bereits beim Wörterbucheintrag berücksichtigt ist, aber noch nicht codiert wurde.
(2) Für die Schritte $i = 1$ bis $i = 3$ ändert sich nichts gegenüber der Teilaufgabe (1).
- Danach gilt:
- $i = 4$: ABA → $\underline{I=4}$, $W(I = 5) =$ ABAB,
- $i = 5$: BA → $\underline{I=3}$, Codierung abgeschlossen, kein neuer Wörterbucheintrag möglich.
(3) Der Vergleich mit obigen Ergebnissen zeigt:
- Das Wörterbuch des Coders weist genau nach $\underline{i=4}$ Codierschritten die gezeigten Einträge auf.
- Beim Decoder ergibt sich demgegenüber eine Zeitverzögerung um einen Schritt: $\underline{i=5}$.
(4) Richtig ist der Lösungsvorschlag 2:
- Die Sonderfallregelung der Decodierung ist (im vorliegenden Beispiel) dann notwendig, wenn im Codierschritt $i$ der Index $I =i$ ausgegeben wird.
- Bei der Decodierung findet er dann die erforderliche Zuordnung „Index → Zeichenfolge” nicht, da das generierte Wörterbuch zum Zeitpunkt $i$ nur Einträge mit Indizes $I < i$ enthält.
- Für die Folge ABABABBAA gilt entsprechend der Teilaufgabe (1) stets $I < i$.
- Dagegen ergäbe sich für die Folge ABABABABA folgende Indizes:
- $$i = 1\hspace{-0.15cm}: \hspace{0.15cm} I = 0\hspace{0.05cm}, \hspace{0.5cm}i = 2\hspace{-0.15cm}: \hspace{0.15cm}I = 1\hspace{0.05cm}, \hspace{0.5cm}i = 3\hspace{-0.15cm}: \hspace{0.15cm}I = 2\hspace{0.05cm}, \hspace{0.5cm}\underline{i = 4\hspace{-0.15cm}: \hspace{0.15cm}I = 4}\hspace{0.05cm}, \hspace{0.5cm}i = 5\hspace{-0.15cm}: \hspace{0.15cm}I = 3\hspace{0.05cm}. $$
Hier noch zusammenfassend die gesamte Decodierung von ABABABABA:
- Die Vorbelegung des Wörterbuchs beinhaltet $(I=0$: A$)$ und $(I=1$: B$)$.
- Dann gilt mit dem Wörterbuch–Array $W(I)$:
- $i = 1$: Decodierung $I=0$ → A,
- $i = 2$: Decodierung $I=1$ → B, $W(I = 2) =$ AB,
- $i = 3$: Decodierung $I=2$ → AB, $W(I = 3) =$ BA,
- $i = 4$: Ein Eintrag mit dem Index $I = 4$ ist nicht vorhanden ⇒ Sonderfallregelung:
Man nimmt das letzte Decodierergebnis $($hier AB$)$ und fügt das erste Zeichen dieser Sequenz hinten an ⇒ ABA.
Danach wird ABA im Wörterbuch unter dem Index $I = 4$ abgelegt. - $i = 5$: Decodierung $I=3$ → BA. Ende der Decoder–Eingangsfolge.