Aufgaben:Aufgabe 3.15: Data Processing Theorem: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2818__Inf_A_3_14.png|right|frame| | + | [[Datei:P_ID2818__Inf_A_3_14.png|right|frame|Zum Data Processing Theorem]] |
Wir betrachten die folgende Datenverarbeitungskette: | Wir betrachten die folgende Datenverarbeitungskette: | ||
| − | * Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ (obere Hälfte in der Grafik) verarbeitet, der durch bedingte Wahrscheinlichkeiten ⇒ $P_{Y|X}(\cdot)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$. | + | * Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ (obere Hälfte in der Grafik) verarbeitet, der durch bedingte Wahrscheinlichkeiten ⇒ $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(\cdot)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$. |
| − | * Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z|Y}(\cdot)$ gegeben (untere Hälfte in der Grafik). $Z$ hängt allein von $Y$ ab ( | + | * Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z\hspace{0.03cm}|\hspace{0.03cm}Y}(\cdot)$ gegeben (untere Hälfte in der Grafik). $Z$ hängt allein von $Y$ ab (deterministisch oder stochastisch) und ist unabhängig von $X$: |
| − | :$$P_{Z\hspace{0. | + | :$$P_{Z\hspace{0.05cm}|\hspace{0.03cm} XY\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} x, y) =P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$ |
| − | + | Für diese Beschreibung wurde folgende Nomenklatur benutzt: | |
:$$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ | :$$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ | ||
| − | Die Verbund–Wahrscheinlichkeitsfunktion (englisch: | + | Die Verbund–Wahrscheinlichkeitsfunktion (englisch: "Joint Probability Mass Function") lautet: |
| − | :$$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0. | + | :$$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.05cm}|\hspace{0.03cm} X\hspace{-0.03cm}}(y\hspace{0.03cm}|\hspace{0.03cm} x)\cdot P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$ |
| − | Das bedeutet auch: $X → Y → Z$ bilden eine [[Stochastische_Signaltheorie/Markovketten|Markovkette]]. Für eine solche gilt das | + | Das bedeutet auch: |
| + | |||
| + | $X → Y → Z$ bilden eine [[Stochastische_Signaltheorie/Markovketten|Markovkette]]. Für eine solche gilt das "Data Processing Theorem" mit folgender Konsequenz: | ||
:$$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$ | :$$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$ | ||
:$$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$ | :$$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$ | ||
Das Theorem besagt somit: | Das Theorem besagt somit: | ||
| − | :* Man kann durch Manipulation ( | + | :* Man kann durch Manipulation ("Processing") der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen. |
| − | :* Datenverarbeitung (durch den Prozessor | + | :* Datenverarbeitung (durch den Prozessor $1$) dient nur dem Zweck, die in $X$ enthaltene Information besser sichtbar zu machen. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. |
| − | * | + | *Bezug genommen wird auch auf die Seite [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Kettenregel_der_Transinformation|Kettenregel der Transinformation]] im vorherigen Kapitel. |
| + | |||
| Zeile 30: | Zeile 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lässt sich das Ergebnis $I(X; Y) = 1 | + | {Wie lässt sich das Ergebnis $I(X; Y) = 1 - H_{\rm bin}(p)$ interpretieren? |
|type="[]"} | |type="[]"} | ||
+ Die Herleitung erfolgt über die Eigenschaften eines streng symmetrischen Kanals. | + Die Herleitung erfolgt über die Eigenschaften eines streng symmetrischen Kanals. | ||
| − | - Ausgenutzt wird, dass $H_{\rm bin}(p)$ eine konkave Funktion ist. | + | - Ausgenutzt wird, dass $H_{\rm bin}(p)$ eine konkave Funktion ist. |
| − | - Das Ergebnis gilt für jede Wahrscheinlichkeitsfunktion $P_X(X)$. | + | - Das Ergebnis gilt für jede Wahrscheinlichkeitsfunktion $P_X(X)$. |
| − | {Welche Transinformation $I(X; Y)$ ergibt sich für den ersten Prozessor mit $p = 0.1$? | + | {Welche Transinformation $I(X; Y)$ ergibt sich für den ersten Prozessor mit $p = 0.1$? |
|type="{}"} | |type="{}"} | ||
$ I(X; Y) \ = \ $ { 0.531 3% } $\ \rm bit$ | $ I(X; Y) \ = \ $ { 0.531 3% } $\ \rm bit$ | ||
| − | {Welche Transinformation $I(Y; Z)$ ergibt sich für den zweiten Prozessor mit $q = 0.2$? | + | {Welche Transinformation $I(Y; Z)$ ergibt sich für den zweiten Prozessor mit $q = 0.2$? |
|type="{}"} | |type="{}"} | ||
$I(Y; Z) \ = \ $ { 0.278 3% } $\ \rm bit$ | $I(Y; Z) \ = \ $ { 0.278 3% } $\ \rm bit$ | ||
| − | {Welche Transinformation $I(X; Z)$ ergibt sich für das Gesamtsystem mit $p = 0.1$ und $q = 0.2$? | + | {Welche Transinformation $I(X; Z)$ ergibt sich für das Gesamtsystem mit $p = 0.1$ und $q = 0.2$? |
|type="{}"} | |type="{}"} | ||
$I(X; Z) \ = \ $ { 0.173 3% } $\ \rm bit$ | $I(X; Z) \ = \ $ { 0.173 3% } $\ \rm bit$ | ||
| − | {Erfüllt dieses Beispiel das | + | {Erfüllt dieses Beispiel das „Data Processing Theorem”? |
| − | |type=" | + | |type="()"} |
+ Ja, | + Ja, | ||
- Nein. | - Nein. | ||
| Zeile 57: | Zeile 65: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig ist nur der <u>Lösungsvorschlag 1</u>: |
| − | $$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{\hspace{0. | + | * Beide Prozessoren beschreiben streng symmetrische Kanäle ⇒ sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend. |
| − | Hierbei ist es völlig egal, ob man von $X = 0$ oder von $X = 1$ ausgeht. Für $X = 0$ erhält man mit $P_{Y|X}(Y = 1|X = 0) = p$ und $P_{Y|X}(Y = 0|X = 0) = 1 – p: | + | * Für einen solchen Binärkanal gilt mit $Y = \{0, 1\} \ ⇒ \ |Y| = 2$: |
| − | $$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, | + | :$$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{Y\hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \hspace{0.05cm}.$$ |
| − | + | *Hierbei ist es völlig egal, ob man von $X = 0$ oder von $X = 1$ ausgeht. | |
| − | Das Ergebnis gilt allerdings nur für $P_X(X) = | + | *Für $X = 0$ erhält man mit $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 1\hspace{0.03cm}|\hspace{0.03cm}X = 0) = p$ und $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 0\hspace{0.03cm}|\hspace{0.03cm}X = 0) = 1 – p\hspace{0.05cm}$: |
| + | :$$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, | ||
| + | \hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | ||
| + | *Das Ergebnis gilt allerdings nur für $P_X(X) = (0.5, \ 0.5)$ ⇒ maximale Transinformation ⇒ Kanalkapazität. | ||
| + | *Andernfalls ist $I(X; Y)$ kleiner. Beispielsweise gilt für $P_X(X) = (1, \ 0)$: $H(X) = 0$ ⇒ $I(X; Y) = 0.$ | ||
| + | *Die binäre Entropiefunktion ist zwar konkav, aber diese Eigenschaft wurde bei der Herleitung nicht benutzt ⇒ Antwort 2 ist falsch. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Für den Prozessor $1$ ergibt sich mit $p = 0.1\hspace{0.05cm}$: | ||
| + | :$$ I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| − | |||
| − | ''' | + | '''(3)''' Entsprechend gilt für den zweiten Prozessor mit $q = 0.2\hspace{0.05cm}$: |
| − | $$ I( | + | :$$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | '''4 | + | '''(4)''' Die Wahrscheinlichkeit für $Z = 0$ unter der Bedingung $X = 0$ ergibt sich über zwei Wege zu |
| − | $$P(\hspace{0.01cm}Z\hspace{-0.05cm} = \hspace{ | + | :$$P(\hspace{0.01cm}Z\hspace{-0.05cm} = 0\hspace{0.03cm} | \hspace{0.03cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$ |
| − | Das Gesamtsystem hat dann die genau gleiche BSC–Struktur wie die Prozessoren $1$ und $2$, aber nun mit der Verfälschungswahrscheinlichkeit | + | *Das Gesamtsystem hat dann die genau gleiche BSC–Struktur wie die Prozessoren $1$ und $2$, aber nun mit der Verfälschungswahrscheinlichkeit $\varepsilon = p + q - 2pq \hspace{0.05cm}.$ |
| − | + | *Für $p = 0.1$ und $q = 0.2$ erhält man: | |
| − | Für $p = 0.1$ und $q = 0.2$ erhält man | + | :$$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$ |
| − | $$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 | ||
| − | |||
| + | '''(5)''' Die Antwort ist natürlich <u>JA</u>, da beim "Data Processing Theorem" genau von den hier gegebenen Voraussetzungen ausgegangen wird. | ||
| − | + | Wir wollen aber zusätzlich einige numerische Ergebnisse auswerten: | |
| − | + | * Gilt $0 ≤ p < 0.5$ und $0 ≤ q < 0.5$, so erhält man: | |
| − | $$varepsilon | + | :$$\varepsilon = p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$ |
| − | $$\varepsilon | + | :$$\varepsilon = q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$ |
| − | + | *Für $p = 0.5$ gilt unabhängig von $q$, da $I(X; Z)$ nicht größer sein kann als $I(X; Y)$: | |
| − | $$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ | + | :$$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ |
| − | Ebenso erhält man mit $q = 0.5$ unabhängig von $p$: | + | *Ebenso erhält man mit $q = 0.5$ unabhängig von $p$: |
| − | $$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ | + | :$$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$ |
| − | Auch für $p < 0.5$ und $q > 0.5$ wird das Data Processing Theorem nicht verletzt, was hier nur an einem Beispiel gezeigt werden soll | + | *Auch für $p < 0.5$ und $q > 0.5$ wird das Data Processing Theorem nicht verletzt, was hier nur an einem Beispiel gezeigt werden soll: |
| − | $$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 | + | ::Mit $p = 0.1$ und $q = 0.8$ erhält man das gleiche Ergebnis wie in Teilaufgabe '''(4)''': |
| − | + | ::$$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 \hspace{0.3cm} | |
| + | \Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 24. September 2021, 12:50 Uhr
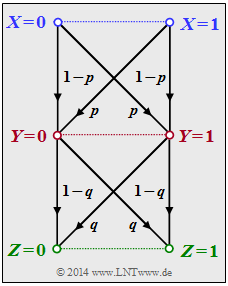
Wir betrachten die folgende Datenverarbeitungskette:
- Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ (obere Hälfte in der Grafik) verarbeitet, der durch bedingte Wahrscheinlichkeiten ⇒ $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(\cdot)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$.
- Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z\hspace{0.03cm}|\hspace{0.03cm}Y}(\cdot)$ gegeben (untere Hälfte in der Grafik). $Z$ hängt allein von $Y$ ab (deterministisch oder stochastisch) und ist unabhängig von $X$:
- $$P_{Z\hspace{0.05cm}|\hspace{0.03cm} XY\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} x, y) =P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$
Für diese Beschreibung wurde folgende Nomenklatur benutzt:
- $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$
Die Verbund–Wahrscheinlichkeitsfunktion (englisch: "Joint Probability Mass Function") lautet:
- $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.05cm}|\hspace{0.03cm} X\hspace{-0.03cm}}(y\hspace{0.03cm}|\hspace{0.03cm} x)\cdot P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$
Das bedeutet auch:
$X → Y → Z$ bilden eine Markovkette. Für eine solche gilt das "Data Processing Theorem" mit folgender Konsequenz:
- $$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$
- $$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$
Das Theorem besagt somit:
- Man kann durch Manipulation ("Processing") der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
- Datenverarbeitung (durch den Prozessor $1$) dient nur dem Zweck, die in $X$ enthaltene Information besser sichtbar zu machen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
- Bezug genommen wird auch auf die Seite Kettenregel der Transinformation im vorherigen Kapitel.
Fragebogen
Musterlösung
- Beide Prozessoren beschreiben streng symmetrische Kanäle ⇒ sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend.
- Für einen solchen Binärkanal gilt mit $Y = \{0, 1\} \ ⇒ \ |Y| = 2$:
- $$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{Y\hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \hspace{0.05cm}.$$
- Hierbei ist es völlig egal, ob man von $X = 0$ oder von $X = 1$ ausgeht.
- Für $X = 0$ erhält man mit $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 1\hspace{0.03cm}|\hspace{0.03cm}X = 0) = p$ und $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 0\hspace{0.03cm}|\hspace{0.03cm}X = 0) = 1 – p\hspace{0.05cm}$:
- $$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, \hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- Das Ergebnis gilt allerdings nur für $P_X(X) = (0.5, \ 0.5)$ ⇒ maximale Transinformation ⇒ Kanalkapazität.
- Andernfalls ist $I(X; Y)$ kleiner. Beispielsweise gilt für $P_X(X) = (1, \ 0)$: $H(X) = 0$ ⇒ $I(X; Y) = 0.$
- Die binäre Entropiefunktion ist zwar konkav, aber diese Eigenschaft wurde bei der Herleitung nicht benutzt ⇒ Antwort 2 ist falsch.
(2) Für den Prozessor $1$ ergibt sich mit $p = 0.1\hspace{0.05cm}$:
- $$ I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$
(3) Entsprechend gilt für den zweiten Prozessor mit $q = 0.2\hspace{0.05cm}$:
- $$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$
(4) Die Wahrscheinlichkeit für $Z = 0$ unter der Bedingung $X = 0$ ergibt sich über zwei Wege zu
- $$P(\hspace{0.01cm}Z\hspace{-0.05cm} = 0\hspace{0.03cm} | \hspace{0.03cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$
- Das Gesamtsystem hat dann die genau gleiche BSC–Struktur wie die Prozessoren $1$ und $2$, aber nun mit der Verfälschungswahrscheinlichkeit $\varepsilon = p + q - 2pq \hspace{0.05cm}.$
- Für $p = 0.1$ und $q = 0.2$ erhält man:
- $$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$
(5) Die Antwort ist natürlich JA, da beim "Data Processing Theorem" genau von den hier gegebenen Voraussetzungen ausgegangen wird.
Wir wollen aber zusätzlich einige numerische Ergebnisse auswerten:
- Gilt $0 ≤ p < 0.5$ und $0 ≤ q < 0.5$, so erhält man:
- $$\varepsilon = p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$
- $$\varepsilon = q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$
- Für $p = 0.5$ gilt unabhängig von $q$, da $I(X; Z)$ nicht größer sein kann als $I(X; Y)$:
- $$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$
- Ebenso erhält man mit $q = 0.5$ unabhängig von $p$:
- $$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$
- Auch für $p < 0.5$ und $q > 0.5$ wird das Data Processing Theorem nicht verletzt, was hier nur an einem Beispiel gezeigt werden soll:
- Mit $p = 0.1$ und $q = 0.8$ erhält man das gleiche Ergebnis wie in Teilaufgabe (4):
- $$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$