Aufgaben:Aufgabe 3.1Z: Einfluss der Nachrichtenphase bei PM: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 3.1Z Einfluss der Phase bei PM nach 3.1Z Einfluss der Nachrichtenphase bei Phasenmodulation) |
|||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
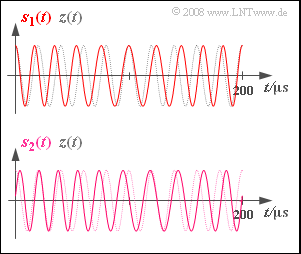
| − | [[Datei:P_ID1080__Mod_Z_3_1.png|right|]] | + | [[Datei:P_ID1080__Mod_Z_3_1.png|right|frame|Zwei PM–Signalverläufe]] |
Wir betrachten die Phasenmodulation verschiedener Schwingungen | Wir betrachten die Phasenmodulation verschiedener Schwingungen | ||
| − | $$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$ | + | :$$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$ |
| − | Das Quellensignal ist hierbei normiert (Amplitude 1) dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann: | + | Das Quellensignal ist hierbei normiert $($Amplitude $1)$ dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann: |
| − | $$s(t) = A_{\rm T} \cdot \cos \ | + | :$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm}\big[\omega_{\rm T} \cdot t + \eta \cdot q(t) \big]\hspace{0.05cm}.$$ |
| − | Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ | + | *Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ϕ_{\rm N} = -90^\circ$ und $η_1 = 2$ charakterisiert. |
| + | *Die Frequenz $f_{\rm N}$ dieses sinusförmigen Quellensignals soll ebenso wie die Trägerfrequenz $f_{\rm T}$ aus dem dargestellten Signalausschnitt der Dauer $200 \ \rm µ s$ ermittelt werden. | ||
| − | Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ | + | *Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ϕ_{\rm N}$ und einen anderen Modulationsindex $η$. Alle anderen Systemparameter sind gegenüber $s_1(t)$ unverändert. |
| − | '' | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Phasenmodulation_(PM)#Signalverl.C3.A4ufe_bei_Phasenmodulation|Signalverläufe bei Phasenmodulation]]. | ||
| + | |||
| Zeile 19: | Zeile 30: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie die Frequenz des Nachrichtensignals. | + | {Ermitteln Sie die Frequenz $f_{\rm N}$ des Nachrichtensignals. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm N} \ = \ $ { 5 3% } $\ \rm kHz$ |
| − | {Wie groß ist die Trägerfrequenz? | + | {Wie groß ist die Trägerfrequenz $f_{\rm T}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm T} \ = \ $ { 50 3% } $\ \rm kHz$ |
| − | {Wie groß ist die maximale Phasenabweichung zwischen $z(t)$ und $s(t)$? | + | {Wie groß ist die maximale Phasenabweichung $ϕ_{\rm max}$ zwischen $z(t)$ und $s(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $ϕ_{max}$ | + | $ϕ_{\rm max} \ = \ $ { 0.318 3% } $\ \rm rad$ |
| − | {Zu welcher Zeitverschiebung der Nulldurchgänge führt diese Phase? | + | {Zu welcher maximalen Zeitverschiebung der Nulldurchgänge führt diese Phase? |
|type="{}"} | |type="{}"} | ||
| − | $Δt_{max}$ | + | $Δt_{\rm max} \ = \ $ { 6.37 3% } $\ \rm µ s$ |
| − | {Bestimmen Sie den Modulationsindex $η_2$ für das Signal $s_2(t). | + | {Bestimmen Sie den Modulationsindex $η_2$ für das Signal $s_2(t)$. |
|type="{}"} | |type="{}"} | ||
| − | $η_2$ | + | $η_2 \ = \ $ { 2 3% } |
| − | {Welche Phasenlage hat das für $s_2(t)$ zugrunde liegende Quellensignal? | + | {Welche Phasenlage $ϕ_{\rm N2}$ hat das für $s_2(t)$ zugrunde liegende Quellensignal $q(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $ϕ_{N2}$ | + | $ϕ_{\rm N2} \ = \ $ { -139--131 } $\ \rm Grad$ |
| Zeile 48: | Zeile 59: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Man erkennt aus der Skizze, dass der dargestellte Signalausschnitt der Dauer $200 \ \rm µ s$ genau der Periodendauer des sinusförmigen Quellensignals entsprechen muss. Daraus folgt $f_{\rm N}\hspace{0.15cm}\underline{ = 5 \ \rm kHz}$. |
| + | *Zu den Zeitpunkten $t = 0$, $t = 100 \ \rm µ s$ und $t = 200 \ \rm µ s$ sind die Signale $z(t)$ und $s(t)$ phasensynchron. | ||
| + | *In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$ ⇒ positive Phase. | ||
| + | *Dagegen ist im Bereich von $t = 100 \ \rm µ s$ bis $t = 200 \ \rm µ s$ die Phase $ϕ(t) < 0$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Es gilt $f_{\rm T}\hspace{0.15cm}\underline{ = 50 \ \rm kHz}$, | ||
| + | *da im dargestellten $z(t)$–Signalausschnitt der Dauer $200 \ \rm µ s$ genau $10$ Perioden abgezählt werden können. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Die maximale relative Phasenabweichung beträgt $ϕ_{\rm max} = η_1/(2π)\hspace{0.15cm}\underline{ ≈ 0.318}$. | ||
| + | |||
| + | |||
| + | '''(4)''' Da die Periodendauer des Trägers $T_0 = 20 \ \rm µ s$ ist, erhält man $Δt_{\rm max} = ϕ_{\rm max} ·T_0\hspace{0.15cm}\underline{ ≈ 6.37 \ \rm µ s}$. | ||
| − | |||
| − | |||
| + | '''(5)''' Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$. | ||
| + | *Daraus kann auf $η_2 = η_1\hspace{0.15cm}\underline{ = 2}$ geschlossen werden. | ||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 \ \rm µ s$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten: |
| − | $$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos | + | :$$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) \big ] = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$ |
| − | Dies entspricht der Phasenlage $ϕ_{N2} = | + | *Dies entspricht der Phasenlage $ϕ_{\rm N2}\hspace{0.15cm}\underline{ = -135^\circ}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 24. März 2020, 17:02 Uhr
Wir betrachten die Phasenmodulation verschiedener Schwingungen
- $$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$
Das Quellensignal ist hierbei normiert $($Amplitude $1)$ dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann:
- $$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm}\big[\omega_{\rm T} \cdot t + \eta \cdot q(t) \big]\hspace{0.05cm}.$$
- Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ϕ_{\rm N} = -90^\circ$ und $η_1 = 2$ charakterisiert.
- Die Frequenz $f_{\rm N}$ dieses sinusförmigen Quellensignals soll ebenso wie die Trägerfrequenz $f_{\rm T}$ aus dem dargestellten Signalausschnitt der Dauer $200 \ \rm µ s$ ermittelt werden.
- Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ϕ_{\rm N}$ und einen anderen Modulationsindex $η$. Alle anderen Systemparameter sind gegenüber $s_1(t)$ unverändert.
Hinweise:
- Die Aufgabe gehört zum Kapitel Phasenmodulation.
- Bezug genommen wird insbesondere auf die Seite Signalverläufe bei Phasenmodulation.
Fragebogen
Musterlösung
- Zu den Zeitpunkten $t = 0$, $t = 100 \ \rm µ s$ und $t = 200 \ \rm µ s$ sind die Signale $z(t)$ und $s(t)$ phasensynchron.
- In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$ ⇒ positive Phase.
- Dagegen ist im Bereich von $t = 100 \ \rm µ s$ bis $t = 200 \ \rm µ s$ die Phase $ϕ(t) < 0$.
(2) Es gilt $f_{\rm T}\hspace{0.15cm}\underline{ = 50 \ \rm kHz}$,
- da im dargestellten $z(t)$–Signalausschnitt der Dauer $200 \ \rm µ s$ genau $10$ Perioden abgezählt werden können.
(3) Die maximale relative Phasenabweichung beträgt $ϕ_{\rm max} = η_1/(2π)\hspace{0.15cm}\underline{ ≈ 0.318}$.
(4) Da die Periodendauer des Trägers $T_0 = 20 \ \rm µ s$ ist, erhält man $Δt_{\rm max} = ϕ_{\rm max} ·T_0\hspace{0.15cm}\underline{ ≈ 6.37 \ \rm µ s}$.
(5) Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$.
- Daraus kann auf $η_2 = η_1\hspace{0.15cm}\underline{ = 2}$ geschlossen werden.
(6) Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 \ \rm µ s$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten:
- $$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) \big ] = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$
- Dies entspricht der Phasenlage $ϕ_{\rm N2}\hspace{0.15cm}\underline{ = -135^\circ}$.