Aufgaben:Aufgabe 3.2Z: Besselspektrum: Unterschied zwischen den Versionen
Aus LNTwww
Tasnad (Diskussion | Beiträge) |
|||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
Beispielsweise kann man das äquivalente Tiefpass–Signal am Ausgang eines Winkelmodulators (PM, FM) in dieser Form darstellen, wenn man geeignete Normierungen vornimmt. | Beispielsweise kann man das äquivalente Tiefpass–Signal am Ausgang eines Winkelmodulators (PM, FM) in dieser Form darstellen, wenn man geeignete Normierungen vornimmt. | ||
| − | Die Fourierreihendarstellung lautet mit $T_0 = 2π/ω_0$: | + | *Die Fourierreihendarstellung lautet mit $T_0 = 2π/ω_0$: |
:$$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$ | :$$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$ | ||
:$$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | :$$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | ||
| − | Diese komplexen Fourierkoeffizienten können mit Hilfe der Besselfunktionen erster Art und | + | *Diese komplexen Fourierkoeffizienten können mit Hilfe der Besselfunktionen erster Art und $n$–ter Ordnung ausgedrückt werden: |
:$${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ | :$${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ | ||
| − | Diese sind in der Grafik im Bereich $0 ≤ η ≤ 5$ dargestellt. Für negative Werte von $n$ erhält man: | + | *Diese sind in der Grafik im Bereich $0 ≤ η ≤ 5$ dargestellt. Für negative Werte von $n$ erhält man: |
:$${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$ | :$${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$ | ||
| − | Die Reihendarstellung der Besselfunktionen lautet: | + | *Die Reihendarstellung der Besselfunktionen lautet: |
:$${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$ | :$${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$ | ||
| − | Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden: | + | *Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden: |
:$${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$ | :$${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Phasenmodulation_(PM)#.C3.84quivalentes_TP.E2.80.93Signal_bei_Phasenmodulation|Äquivalentes Tiefpass-Signal bei Phasenmodulation]]. | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Phasenmodulation_(PM)#.C3.84quivalentes_TP.E2.80.93Signal_bei_Phasenmodulation|Äquivalentes Tiefpass-Signal bei Phasenmodulation]]. |
*Die Werte der Besselfunktionen findet man in Formelsammlungen in tabellarischer Form. | *Die Werte der Besselfunktionen findet man in Formelsammlungen in tabellarischer Form. | ||
| − | *Sie können zur Lösung dieser Aufgabe auch das | + | *Sie können zur Lösung dieser Aufgabe auch das interaktive Applet [[Applets:Besselfunktionen_erster_Art| Besselfunktion erster Art]] benutzen. |
| − | + | ||
| Zeile 34: | Zeile 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Eigenschaften besitzt das Signal x(t)? | + | {Welche Eigenschaften besitzt das Signal $x(t)$? |
|type="[]"} | |type="[]"} | ||
| − | - $x(t)$ ist für alle Zeiten t imaginär. | + | - $x(t)$ ist für alle Zeiten $t$ imaginär. |
| − | + x(t) ist | + | + $x(t)$ ist periodisch. |
| − | - Die Spektralfunktion $X(f)$ erhält man über das | + | - Die Spektralfunktion $X(f)$ erhält man über das Fourierintegral. |
| − | {Schreiben Sie die Fourierkoeffizienten $D_n$ mit den Besselfunktionen erster Art. Welche Zusammenhänge sind zu erkennen? | + | {Schreiben Sie die Fourierkoeffizienten $D_n$ mit den Besselfunktionen erster Art ⇒ ${\rm J}_n(η)$. Welche Zusammenhänge sind zu erkennen? |
|type="[]"} | |type="[]"} | ||
| − | - Alle $D_n$ sind gleich $ | + | - Alle $D_n$ sind gleich ${\rm J}_η(0)$. |
| − | + Es gilt $D_n = | + | + Es gilt $D_n = {\rm J}_n(η)$. |
| − | - Es gilt $D_n = | + | - Es gilt $D_n = -{\rm J}_η(n)$. |
{ Welche Eigenschaften besitzen die Fourierkoeffizienten? | { Welche Eigenschaften besitzen die Fourierkoeffizienten? | ||
| − | |type=" | + | |type="()"} |
| − | + Alle $D_n$ sind rein reell. | + | + Alle $D_n$ sind rein reell. |
| − | - Alle $D_n$ sind rein imaginär. | + | - Alle $D_n$ sind rein imaginär. |
| − | {Für $η = 2$ lauten die Koeffizienten $D_0 = 0.224$ und $D_1 = 0.577$. Berechnen Sie hieraus die Koeffizienten $D_2$ und $D_3$. | + | {Für $η = 2$ lauten die Koeffizienten $D_0 = 0.224$ und $D_1 = 0.577$. Berechnen Sie hieraus die Koeffizienten $D_2$ und $D_3$. |
|type="{}"} | |type="{}"} | ||
| − | $D_2$ | + | $D_2 \ = \ $ { 0.353 3% } |
| − | $D_3$ | + | $D_3 \ = \ $ { 0.129 3% } |
| − | {Wie lauten die Fourierkoeffizienten $D_{ | + | {Wie lauten die Fourierkoeffizienten $D_{-2}$ und $D_{-3}$ ? |
|type="{}"} | |type="{}"} | ||
| − | $D_{ | + | $D_{-2} \ = \ $ { 0.353 3% } |
| − | $D_{ | + | $D_{-3} \ = \ $ { -0.133--0.125 } |
| Zeile 66: | Zeile 72: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig ist nur der <u>zweite Lösungsvorschlag</u>: |
| − | Mit $T_0 = 2π/ω_0$ gilt beispielsweise: | + | *$x(t)$ ist ein komplexes Signal, das nur in Ausnahmefällen reell wird, zum Beispiel zur Zeit $t = 0$. |
| − | $$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } = | + | *Ein rein imaginärer Wert (zu gewissen Zeiten) kann sich nur dann ergeben, wenn $η ≥ π/2$ ist ⇒ Antwort 1 ist falsch. |
| − | + | *Mit $T_0 = 2π/ω_0$ gilt beispielsweise: | |
| − | Dieses Signal ist | + | :$$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } = |
| + | {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} + \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi) } ={\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} ) } = x(t)\hspace{0.05cm}.$$ | ||
| + | *Dieses Signal ist periodisch. Zur Berechnung der Spektralfunktion muss die Fourierreihe und nicht das Fourierintegral herangezogen werden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Die Fourierkoeffizienten lauten: | ||
| + | :$$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t) }\cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | ||
| + | *Durch Zusammenfassen der beiden Terme und nach der Substitution $α = ω_0 · t$ erhält man: | ||
| + | :$$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm} = {\rm J}_n (\eta) .$$ | ||
| + | *Richtig ist also der <u>zweite Lösungsvorschlag</u>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' Mit dem Satz von Euler können die Fourierkoeffizienten wie folgt dargestellt werden: | ||
| + | :$$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha + | ||
| + | \frac{\rm j}{2\pi}\cdot \int_{-\pi}^{+\pi} {\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ | ||
| + | *Der Integrand des ersten Integrals ist eine gerade Funktion von $\alpha$: | ||
| + | :$$I_1 (-\alpha) = {\cos( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\cos( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= | ||
| + | {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = I_1 (\alpha) \hspace{0.05cm}.$$ | ||
| + | *Dagegen ist der zweite Integrand eine ungerade Funktion: | ||
| + | :$$I_2 (-\alpha) = {\sin( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\sin( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= | ||
| + | -{\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = -I_2 (\alpha) \hspace{0.05cm}.$$ | ||
| + | *Somit verschwindet das zweite Integral und man erhält unter Berücksichtigung der Symmetrie: | ||
| + | :$$D_n = \frac{1}{\pi}\cdot \int_{0}^{\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ | ||
| + | *Richtig ist somit der <u>Lösungsvorschlag 1</u>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''4 | + | '''(4)''' Entsprechend der iterativen Berechnungsformel gilt für $η = 2$: |
| − | $$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$ | + | :$$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$ |
| − | $$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$ | + | :$$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$ |
| − | '''5 | + | '''(5)''' Aufgrund der angegebenen Symmetriebeziehung gilt weiter: |
| + | :$$ D_{–2} = D_2\hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$ | ||
| + | :$$D_{–3} = -D_3 \hspace{0.15cm}\underline {= -0.129} \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 10. Juni 2020, 09:03 Uhr
Wir betrachten das komplexe Signal
- $$x(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t) }\hspace{0.05cm}.$$
Beispielsweise kann man das äquivalente Tiefpass–Signal am Ausgang eines Winkelmodulators (PM, FM) in dieser Form darstellen, wenn man geeignete Normierungen vornimmt.
- Die Fourierreihendarstellung lautet mit $T_0 = 2π/ω_0$:
- $$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Diese komplexen Fourierkoeffizienten können mit Hilfe der Besselfunktionen erster Art und $n$–ter Ordnung ausgedrückt werden:
- $${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
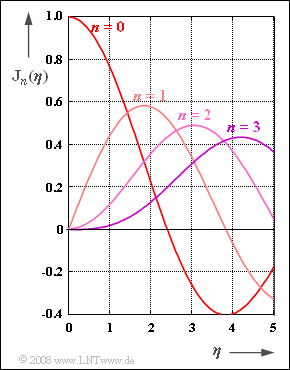
- Diese sind in der Grafik im Bereich $0 ≤ η ≤ 5$ dargestellt. Für negative Werte von $n$ erhält man:
- $${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$
- Die Reihendarstellung der Besselfunktionen lautet:
- $${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$
- Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden:
- $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Phasenmodulation.
- Bezug genommen wird insbesondere auf die Seite Äquivalentes Tiefpass-Signal bei Phasenmodulation.
- Die Werte der Besselfunktionen findet man in Formelsammlungen in tabellarischer Form.
- Sie können zur Lösung dieser Aufgabe auch das interaktive Applet Besselfunktion erster Art benutzen.
Fragebogen
Musterlösung
(1) Richtig ist nur der zweite Lösungsvorschlag:
- $x(t)$ ist ein komplexes Signal, das nur in Ausnahmefällen reell wird, zum Beispiel zur Zeit $t = 0$.
- Ein rein imaginärer Wert (zu gewissen Zeiten) kann sich nur dann ergeben, wenn $η ≥ π/2$ ist ⇒ Antwort 1 ist falsch.
- Mit $T_0 = 2π/ω_0$ gilt beispielsweise:
- $$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} + \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi) } ={\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} ) } = x(t)\hspace{0.05cm}.$$
- Dieses Signal ist periodisch. Zur Berechnung der Spektralfunktion muss die Fourierreihe und nicht das Fourierintegral herangezogen werden.
(2) Die Fourierkoeffizienten lauten:
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t) }\cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Durch Zusammenfassen der beiden Terme und nach der Substitution $α = ω_0 · t$ erhält man:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm} = {\rm J}_n (\eta) .$$
- Richtig ist also der zweite Lösungsvorschlag.
(3) Mit dem Satz von Euler können die Fourierkoeffizienten wie folgt dargestellt werden:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha + \frac{\rm j}{2\pi}\cdot \int_{-\pi}^{+\pi} {\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- Der Integrand des ersten Integrals ist eine gerade Funktion von $\alpha$:
- $$I_1 (-\alpha) = {\cos( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\cos( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = I_1 (\alpha) \hspace{0.05cm}.$$
- Dagegen ist der zweite Integrand eine ungerade Funktion:
- $$I_2 (-\alpha) = {\sin( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\sin( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= -{\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = -I_2 (\alpha) \hspace{0.05cm}.$$
- Somit verschwindet das zweite Integral und man erhält unter Berücksichtigung der Symmetrie:
- $$D_n = \frac{1}{\pi}\cdot \int_{0}^{\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- Richtig ist somit der Lösungsvorschlag 1.
(4) Entsprechend der iterativen Berechnungsformel gilt für $η = 2$:
- $$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$
(5) Aufgrund der angegebenen Symmetriebeziehung gilt weiter:
- $$ D_{–2} = D_2\hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_{–3} = -D_3 \hspace{0.15cm}\underline {= -0.129} \hspace{0.05cm}.$$