Aufgaben:Aufgabe 4.12: Wurzel–Nyquist–Systeme: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1722__Mod_A_4_11.png|right|frame|Spektren von Sendegrundimpuls und Detektionsgrundimpuls]] | + | [[Datei:P_ID1722__Mod_A_4_11.png|right|frame|Spektren von Sendegrundimpuls <br>und Detektionsgrundimpuls]] |
| − | Bei | + | Bei Quadraturamplitudenmodulationssystemen wird häufig anstelle eines rechteckförmigen Sendegrundimpulses die "Wurzel–Nyquist–Variante" gewählt, wobei dieser Name aus dem Spektralbereich abgeleitet ist. Der Grund hierfür ist die signifikant kleinere Bandbreite. |
| + | |||
| + | *In diesem Fall erfüllt der Detektionsgrundimpuls $g_d(t)$ die [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Frequenzbereich|erste Nyquistbedingung]], da $G_d(f)$ punktsymmetrisch um die so genannte Nyquistfrequenz $f_{\rm Nyq} = 1/T$ ist. | ||
| + | *Die Spektralfunktion $G_d(f)$ ist ein [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Cosinus-Rolloff-Tiefpass|Cosinus–Rolloff–Spektrum]], wobei der Rolloff–Faktor $r$ Werte zwischen $0$ und $1$ (einschließlich dieser Grenzen) annehmen kann. | ||
| − | |||
Weiterhin gilt für den Nyquist–Frequenzgang: | Weiterhin gilt für den Nyquist–Frequenzgang: | ||
| − | * Für $|f| < f_1 = f_{Nyq} · (1 – r)$ ist $G_d(f)$ konstant gleich $g_0 · T$. | + | * Für $|f| < f_1 = f_{\rm Nyq} · (1 – r)$ ist $G_d(f)$ konstant gleich $g_0 · T$. |
| − | * Bei Frequenzen größer als $f_2 = f_{Nyq} · (1 + r)$ hat $G_d(f)$ keine Anteile. | + | * Bei Frequenzen größer als $f_2 = f_{\rm Nyq} · (1 + r)$ hat $G_d(f)$ keine Anteile. |
* Dazwischen verläuft die Flanke cosinusförmig. | * Dazwischen verläuft die Flanke cosinusförmig. | ||
| − | Die Optimierung digitaler Nachrichtenübertragungssysteme ergibt, dass der Empfängerfrequenzgang $H_{\rm E}(f)$ formgleich mit dem Sendespektrum $G_s(f)$ sein sollte. Um dimensionsrichtige Spektralfunktionen zu erhalten, wird für diese Aufgabe und die Grafik vorausgesetzt: | + | |
| + | Die Optimierung digitaler Nachrichtenübertragungssysteme ergibt, dass der Empfängerfrequenzgang $H_{\rm E}(f)$ formgleich mit dem Sendespektrum $G_s(f)$ sein sollte. | ||
| + | |||
| + | Um dimensionsrichtige Spektralfunktionen zu erhalten, wird für diese Aufgabe und die Grafik vorausgesetzt: | ||
:$$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},\hspace{0.4cm} H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$ | :$$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},\hspace{0.4cm} H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$ | ||
| − | Die obere Grafik zeigt das Sendespektrum $G_s(f)$ für die Rolloff–Faktoren | + | Die obere Grafik zeigt das Sendespektrum $G_s(f)$ für die Rolloff–Faktoren |
| − | *$r = 0$ (grün punktiertes Rechteck), | + | *$r = 0$ (grün punktiertes Rechteck), |
| − | *$r = 0.5$ (blaue durchgezogene | + | *$r = 0.5$ (blaue durchgezogene Kurve), |
| − | *$r = 1$ ( | + | *$r = 1$ (rote gestrichelte Kurve). |
| − | Unten ist das Spektrum $G_d(f)$ vor dem Entscheider in gleichen Farben dargestellt. Der dazugehörige Impuls $g_d(t)$ ist für alle gültigen Rolloff–Faktoren ( | + | Unten ist das Spektrum $G_d(f)$ vor dem Entscheider in gleichen Farben dargestellt. |
| + | *Der dazugehörige Impuls $g_d(t)$ ist für alle gültigen Rolloff–Faktoren $(0 ≤ r ≤ 1)$ ein [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Zeitbereich|Nyquistimpuls]] im Gegensatz zum Sendegrundimpuls $g_s(t)$. | ||
| + | *Für diesen wird in der Literatur – zum Beispiel in '''[Kam04]''' – folgende Gleichung angegeben: | ||
:$$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$ | :$$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''[Kam04]''' | + | |
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation|"Quadratur–Amplitudenmodulation"]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Quadratur–Amplitudenmodulation#Nyquist.E2.80.93_und_Wurzel.E2.80.93Nyquist.E2.80.93QAM.E2.80.93Systeme|"Nyquist- und Wurzel-Nyquist-Systeme"]] in diesem Kapitel. | ||
| + | *Weitere hilfreiche Informationen erfahren Sie im Kapitel [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen|"Eigenschaften von Nyquistsystemen"]] des Buches „Digitalsignalübertragung”. | ||
| + | * '''[Kam04]''' verweist auf das Fachbuch „Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004”. | ||
| + | *Energien sind in $\rm V^2s$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$. | ||
| + | |||
| + | |||
| Zeile 44: | Zeile 49: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet der Sendegrundimpuls $g_s(t)$ für den Rolloff–Faktor r = 0? Welcher Signalwert ergibt sich zum Zeitpunkt t = 0? | + | {Wie lautet der Sendegrundimpuls $g_s(t)$ für den Rolloff–Faktor $r = 0$? Welcher Signalwert ergibt sich zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1 3% } $\ \cdot g_0$ |
| − | {Wie lautet der Sendegrundimpuls $g_s(t)$ für den Rolloff–Faktor r = 1? Welcher Signalwert ergibt sich zum Zeitpunkt t = 0? | + | {Wie lautet der Sendegrundimpuls $g_s(t)$ für den Rolloff–Faktor $r = 1$? Welcher Signalwert ergibt sich zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1.273 3% } $\ \cdot g_0$ |
| − | {Es gelte weiter r = 1. Zu welchen Zeiten hat $g_s(t)$ Nulldurchgänge? | + | {Es gelte weiter $r = 1$. Zu welchen Zeiten hat $g_s(t)$ Nulldurchgänge? |
| − | |type=" | + | |type="()"} |
| − | - Bei allen Vielfachen der Symboldauer T | + | - Bei allen Vielfachen der Symboldauer $T$. |
| − | - Bei t = ±0.25 T, ±0.75 T, ±1.25 T, ±1.75 T, ... | + | - Bei $t = ±0.25 T, \ ±0.75 T, \ ±1.25 T, \ ±1.75 T$, ... |
| − | + Bei t = ±0.75 T, ±1.25 T, ±1.75 T, ... | + | + Bei $t = ±0.75 T, \ ±1.25 T,\ ±1.75 T$, ... |
| − | { | + | {Wie lautet der Sendegrundimpuls $g_s(t)$ für den Rolloff–Faktor $r = 0.5$? Welcher Signalwert ergibt sich zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $g_s(t = 0) \ = \ $ { 1.137 3% } $\ \cdot g_0$ |
| − | {Welche Aussagen sind für die Signalamplitude unabhängig von r gültig? Lösen Sie diese | + | {Welche Aussagen sind für die Signalamplitude unabhängig von $r$ gültig? Lösen Sie diese Teilaufgabe im Frequenzbereich. |
| − | |type=" | + | |type="()"} |
| − | - | + | - Die Sendeimpulsamplitude kann alle Werte im Bereich $0 ≤ g_s(t = 0) ≤ g_0$ annehmen. |
| − | - | + | - Die Sendeimpulsamplitude kann alle Werte im Bereich $g_0 ≤ g_s(t = 0) ≤ 2 g_0$ annehmen. |
| − | + | + | + Die Sendeimpulsamplitude kann alle Werte im Bereich $g_0 ≤ g_s(t = 0) ≤ 4 g_0/π$ annehmen. |
| − | {Wie groß ist die Energie des Sendegrundimpulses $g_s(t)$ für r = 0 und r = 1? | + | {Wie groß ist die Energie $E_{g_s}$ des Sendegrundimpulses $g_s(t)$ für $r = 0$ und $r = 1$? |
|type="{}"} | |type="{}"} | ||
| − | $ r = 0: | + | $r = 0\text{:} \ \ \ \ E_{g_s} \ = \ $ { 1 3% } $\ \cdot g_0^2 \cdot T$ |
| − | $ r = 1: | + | $r = 1\text{:} \ \ \ \ E_{g_s} \ = \ $ { 1 3% } $\ \cdot g_0^2 \cdot T$ |
</quiz> | </quiz> | ||
| Zeile 77: | Zeile 82: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Setzt man in die gegebene Gleichung $r = 0$ ein, so verschwinden im Zähler und Nenner die jeweils ersten Terme und man erhält: |
| − | $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm si} \left (\pi \cdot {t}/{T} \right )\hspace{0.05cm}.$$ | + | : $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm si} \left (\pi \cdot {t}/{T} \right )\hspace{0.05cm}.$$ |
| − | Zum Zeitpunkt t = 0 ist der | + | *Zum Zeitpunkt $t = 0$ ist der $\rm si$–Impuls gleich $g_0$: |
| − | $$ g_s(t) \hspace{0.15cm}\underline { = 1. | + | :$$ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Für $r = 1$ lässt sich die angegebene Gleichung wie folgt vereinfachen: | ||
| + | :$$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist der <u>letzte Lösungsvorschlag</u>: | ||
| + | *Nulldurchgänge sind für $r = 1$ nur möglich, wenn die Cosinusfunktion im Zähler Null ist, also für alle ganzzahligen Werte von $k$: | ||
| + | :$$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$ | ||
| + | *Richtig ist aber nur der letzte Lösungsvorschlag, da die Nullstellen bei $±0.25T$ durch die Nullstelle im Nenner aufgehoben werden. | ||
| + | *Die Anwendung der Regel von de l'Hospital liefert $g_s(t = ± 0.25T) = g_0$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Mit $r = 0.5$ und der Abkürzung $x = t/T$ erhält man: | ||
| + | :$$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *Für die Berechnung zum Zeitpunkt $t = 0$ muss die Regel von de l'Hospital angewandt werden. | ||
| + | *Die Ableitungen von Zähler und Nenner ergeben: | ||
| + | :$$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$ | ||
| + | [[Datei:P_ID1723__Mod_A_4_11b.png|right|frame|Sendegrundimpuls (Wurzel–Nyquist, oben), <br>Detektionsgrundimpuls (Nyquist, unten)]] | ||
| + | |||
| + | :$$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$ | ||
| + | *Die beiden Grenzübergänge für $x → 0$ liefern: | ||
| + | :$$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$ | ||
| + | *Damit gilt für die Signalamplitude zum Zeitpunkt $t = 0$: | ||
| + | :$$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Grafik verdeutlicht nochmals die hier berechneten Ergebnisse: | ||
| + | *$g_d(t)$ ist ein Nyquistimpuls, das heißt, dass er zumindest bei allen Vielfachen der Symboldauer $T$ Nulldurchgänge besitzt (je nach Rolloff–Faktor noch andere Nullstellen). | ||
| + | *$g_s(t)$ erfüllt dagegen nicht die Nyquistbedingung. Außerdem erkennt man aus dieser Darstellung nochmals, dass für $r ≠ 0$ die Impulsamplitude $g_s(t = 0)$ stets größer als $g_0$ ist. | ||
| + | |||
| + | |||
| − | |||
| − | |||
| − | ''' | + | '''(5)''' Richtig ist der <u>letzte Lösungsvorschlag</u> $($der erste Lösungsvorschlag scheidet bereits nach den Ergebnissen der Teilaufgaben '''(2)''' und '''(4)''' aus$)$. |
| − | |||
| − | Richtig ist | ||
| − | + | Die Gültigkeit der unteren Schranke $g_0$ und der oberen Schranke $4g_0/π$ lässt sich wie folgt nachweisen: | |
| − | $$g_s( | + | * Die Impulsamplitude $g_s(t = 0)$ ist grundsätzlich gleich der Fläche unter der Spektralfunktion $G_s(f)$. |
| + | * Die kleinste Fläche ergibt sich für $r = 0$. Hier ist $G_s(f) = g_0 · T$ im Bereich $|f| < ±1/(2T)$. Die Fläche ist somit gleich $g_0$. | ||
| + | * Die größte Fläche ergibt sich für $r = 1$. Hier ist $G_s(f)$ auf den Bereich $±1/T$ ausgedehnt und hat einen cosinusförmigen Verlauf. | ||
| + | *Das Ergebnis $g_s(t = 0) = 4g_0/π$ wurde bereits in Teilaufgabe '''(3)''' berechnet. Es gilt aber auch: | ||
| + | :$$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' Die Energie des Sendegrundimpulses $g_s(t)$ kann man nach dem Satz von Parseval im Zeit– oder auch im Frequenzbereich ermitteln: |
| − | $$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ | + | :$$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ |
| − | Aus den Gleichungen und der Grafik auf der Angabenseite erkennt man, dass $|G_s(f)|^2$ formgleich mit $G_d(f)$ ist, mit dem Unterschied, dass die Höhe ( | + | *Aus den Gleichungen und der Grafik auf der Angabenseite erkennt man, dass $|G_s(f)|^2$ formgleich mit $G_d(f)$ ist, <br>mit dem Unterschied, dass die Höhe nun $(g_0 · T)^2$ anstelle von $g_0 · T$ ist: |
| − | $$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ | + | :$$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$ |
| − | Aufgrund der Nyquistform von $G_d(f)$ gilt aber unabhängig von r: | + | *Aufgrund der Nyquistform von $G_d(f)$ gilt aber unabhängig von $r$: |
| − | $$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$ | + | :$$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$ |
| − | Damit ist die Impulsenergie unabhängig von r, also auch gültig für r = 0 und r = 1 | + | *Damit ist auch die Impulsenergie unabhängig von $r$, also auch gültig für $r = 0$ und $r = 1$. In <u>beiden Fällen</u> ist $E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 19. April 2022, 15:27 Uhr
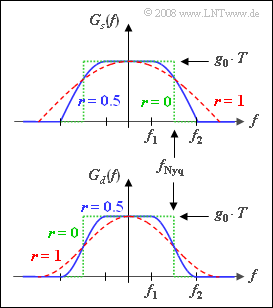
Bei Quadraturamplitudenmodulationssystemen wird häufig anstelle eines rechteckförmigen Sendegrundimpulses die "Wurzel–Nyquist–Variante" gewählt, wobei dieser Name aus dem Spektralbereich abgeleitet ist. Der Grund hierfür ist die signifikant kleinere Bandbreite.
- In diesem Fall erfüllt der Detektionsgrundimpuls $g_d(t)$ die erste Nyquistbedingung, da $G_d(f)$ punktsymmetrisch um die so genannte Nyquistfrequenz $f_{\rm Nyq} = 1/T$ ist.
- Die Spektralfunktion $G_d(f)$ ist ein Cosinus–Rolloff–Spektrum, wobei der Rolloff–Faktor $r$ Werte zwischen $0$ und $1$ (einschließlich dieser Grenzen) annehmen kann.
Weiterhin gilt für den Nyquist–Frequenzgang:
- Für $|f| < f_1 = f_{\rm Nyq} · (1 – r)$ ist $G_d(f)$ konstant gleich $g_0 · T$.
- Bei Frequenzen größer als $f_2 = f_{\rm Nyq} · (1 + r)$ hat $G_d(f)$ keine Anteile.
- Dazwischen verläuft die Flanke cosinusförmig.
Die Optimierung digitaler Nachrichtenübertragungssysteme ergibt, dass der Empfängerfrequenzgang $H_{\rm E}(f)$ formgleich mit dem Sendespektrum $G_s(f)$ sein sollte.
Um dimensionsrichtige Spektralfunktionen zu erhalten, wird für diese Aufgabe und die Grafik vorausgesetzt:
- $$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},\hspace{0.4cm} H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$
Die obere Grafik zeigt das Sendespektrum $G_s(f)$ für die Rolloff–Faktoren
- $r = 0$ (grün punktiertes Rechteck),
- $r = 0.5$ (blaue durchgezogene Kurve),
- $r = 1$ (rote gestrichelte Kurve).
Unten ist das Spektrum $G_d(f)$ vor dem Entscheider in gleichen Farben dargestellt.
- Der dazugehörige Impuls $g_d(t)$ ist für alle gültigen Rolloff–Faktoren $(0 ≤ r ≤ 1)$ ein Nyquistimpuls im Gegensatz zum Sendegrundimpuls $g_s(t)$.
- Für diesen wird in der Literatur – zum Beispiel in [Kam04] – folgende Gleichung angegeben:
- $$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Quadratur–Amplitudenmodulation".
- Bezug genommen wird insbesondere auf die Seite "Nyquist- und Wurzel-Nyquist-Systeme" in diesem Kapitel.
- Weitere hilfreiche Informationen erfahren Sie im Kapitel "Eigenschaften von Nyquistsystemen" des Buches „Digitalsignalübertragung”.
- [Kam04] verweist auf das Fachbuch „Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004”.
- Energien sind in $\rm V^2s$ anzugeben; sie beziehen sich somit auf den Bezugswiderstand $R = 1 \ \rm \Omega$.
Fragebogen
Musterlösung
- $$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm si} \left (\pi \cdot {t}/{T} \right )\hspace{0.05cm}.$$
- Zum Zeitpunkt $t = 0$ ist der $\rm si$–Impuls gleich $g_0$:
- $$ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$$
(2) Für $r = 1$ lässt sich die angegebene Gleichung wie folgt vereinfachen:
- $$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$
(3) Richtig ist der letzte Lösungsvorschlag:
- Nulldurchgänge sind für $r = 1$ nur möglich, wenn die Cosinusfunktion im Zähler Null ist, also für alle ganzzahligen Werte von $k$:
- $$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$
- Richtig ist aber nur der letzte Lösungsvorschlag, da die Nullstellen bei $±0.25T$ durch die Nullstelle im Nenner aufgehoben werden.
- Die Anwendung der Regel von de l'Hospital liefert $g_s(t = ± 0.25T) = g_0$.
(4) Mit $r = 0.5$ und der Abkürzung $x = t/T$ erhält man:
- $$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$
- Für die Berechnung zum Zeitpunkt $t = 0$ muss die Regel von de l'Hospital angewandt werden.
- Die Ableitungen von Zähler und Nenner ergeben:
- $$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$
- $$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$
- Die beiden Grenzübergänge für $x → 0$ liefern:
- $$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$
- Damit gilt für die Signalamplitude zum Zeitpunkt $t = 0$:
- $$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$
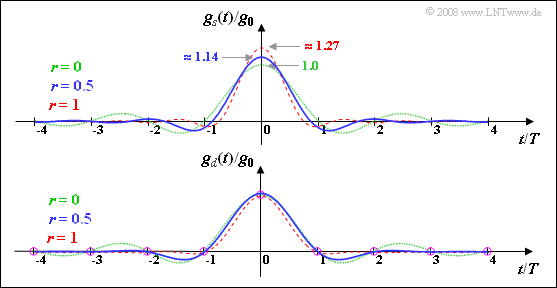
Die Grafik verdeutlicht nochmals die hier berechneten Ergebnisse:
- $g_d(t)$ ist ein Nyquistimpuls, das heißt, dass er zumindest bei allen Vielfachen der Symboldauer $T$ Nulldurchgänge besitzt (je nach Rolloff–Faktor noch andere Nullstellen).
- $g_s(t)$ erfüllt dagegen nicht die Nyquistbedingung. Außerdem erkennt man aus dieser Darstellung nochmals, dass für $r ≠ 0$ die Impulsamplitude $g_s(t = 0)$ stets größer als $g_0$ ist.
(5) Richtig ist der letzte Lösungsvorschlag $($der erste Lösungsvorschlag scheidet bereits nach den Ergebnissen der Teilaufgaben (2) und (4) aus$)$.
Die Gültigkeit der unteren Schranke $g_0$ und der oberen Schranke $4g_0/π$ lässt sich wie folgt nachweisen:
- Die Impulsamplitude $g_s(t = 0)$ ist grundsätzlich gleich der Fläche unter der Spektralfunktion $G_s(f)$.
- Die kleinste Fläche ergibt sich für $r = 0$. Hier ist $G_s(f) = g_0 · T$ im Bereich $|f| < ±1/(2T)$. Die Fläche ist somit gleich $g_0$.
- Die größte Fläche ergibt sich für $r = 1$. Hier ist $G_s(f)$ auf den Bereich $±1/T$ ausgedehnt und hat einen cosinusförmigen Verlauf.
- Das Ergebnis $g_s(t = 0) = 4g_0/π$ wurde bereits in Teilaufgabe (3) berechnet. Es gilt aber auch:
- $$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$
(6) Die Energie des Sendegrundimpulses $g_s(t)$ kann man nach dem Satz von Parseval im Zeit– oder auch im Frequenzbereich ermitteln:
- $$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$
- Aus den Gleichungen und der Grafik auf der Angabenseite erkennt man, dass $|G_s(f)|^2$ formgleich mit $G_d(f)$ ist,
mit dem Unterschied, dass die Höhe nun $(g_0 · T)^2$ anstelle von $g_0 · T$ ist:
- $$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$
- Aufgrund der Nyquistform von $G_d(f)$ gilt aber unabhängig von $r$:
- $$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$
- Damit ist auch die Impulsenergie unabhängig von $r$, also auch gültig für $r = 0$ und $r = 1$. In beiden Fällen ist $E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$