Aufgaben:Aufgabe 4.12Z: Nochmals 4–QAM–Systeme: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID1724__Mod_Z_4_11.png|right|frame|Phasendiagramme bei 4–QAM, ideal und mit Degradationen]] | [[Datei:P_ID1724__Mod_Z_4_11.png|right|frame|Phasendiagramme bei 4–QAM, ideal und mit Degradationen]] | ||
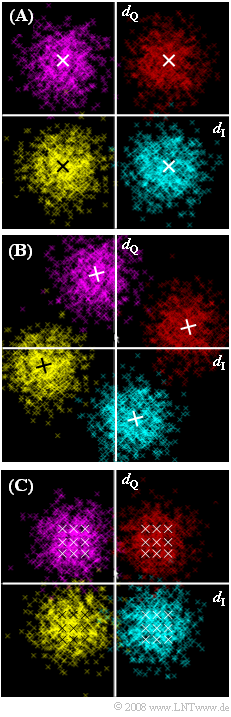
| − | Die Grafik | + | Die Grafik $\rm (A)$ zeigt das Phasendiagramm der 4–QAM nach dem Matched–Filter, wobei eine bei AWGN–Rauschen unter der Nebenbedingung „Spitzenwertbegrenzung” optimale Realisierungsform gewählt wurde: |
| − | * rechteckförmiger Sendegrundimpuls der Symboldauer $T$, | + | * rechteckförmiger Sendegrundimpuls der Symboldauer $T$, |
| − | * rechteckförmige Impulsantwort des Matched-Filters gleicher Breite $T$. | + | * rechteckförmige Impulsantwort des Matched-Filters gleicher Breite $T$. |
| − | |||
| − | Es liegt hier ein AWGN–Kanal mit $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ vor. Entsprechend gilt für die Bitfehlerwahrscheinlichkeit des zunächst betrachteten Systems | + | Alle hier dargestellten Phasendiagramme – sowohl $\rm (A)$ als auch $\rm (B)$ und $\rm (C)$ – beziehen sich ausschließlich auf die Detektionszeitpunkte. Die Übergänge zwischen den einzelnen zeitdiskreten Punkten sind in diesem Phasendiagrammen also nicht eingezeichnet. |
| + | |||
| + | *Es liegt hier ein AWGN–Kanal mit $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ vor. | ||
| + | *Entsprechend gilt für die Bitfehlerwahrscheinlichkeit des zunächst betrachteten Systems $\rm (A)$ : | ||
:$$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$ | :$$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$ | ||
| − | Die Phasendiagramme | + | Die Phasendiagramme $\rm (B)$ und $\rm (C)$ gehören zu zwei Systemen, bei denen die 4–QAM nicht optimal realisiert wurde. Auch bei diesen ist wieder jeweils AWGN–Rauschen mit $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ vorausgesetzt. |
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hinweise: | |
| − | $${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$ | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation|Quadratur–Amplitudenmodulation]]. |
| + | *Bezug genommen wird insbesondere auf die Seite [[Digitalsignalübertragung/Lineare_digitale_Modulation_–_Kohärente_Demodulation#Phasenversatz_zwischen_Sender_und_Empf.C3.A4nger|"Phasenversatz zwischen Sender und Empfänger"]] im Buch „Digitalsignalübertragung”. | ||
| + | *Die Ursachen und Auswirkungen von Impulsinterferenzen werden im [[Digitalsignalübertragung/Ursachen_und_Auswirkungen_von_Impulsinterferenzen|gleichnamigen Abschnitt]] des Buches „Digitalsignalübertragung” erläutert. | ||
| + | *Die Kreuze in den Grafiken markieren mögliche Punkte in den Diagrammen, wenn kein AWGN–Rauschen vorhanden wäre. | ||
| + | *Die Punktwolken aufgrund des AWGN–Rauschens haben alle gleichen Durchmesser. Die rote Wolke erscheint nur deshalb etwas kleiner als die anderen, da „Rot” auf „Schwarz” schlechter zu erkennen ist. | ||
| + | *Als eine hinreichend gute Näherung für das komplementäre Gaußsche Fehlerintegral können Sie verwenden: | ||
| + | :$${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$ | ||
| Zeile 33: | Zeile 36: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie mit der angegebenen Näherung die | + | {Berechnen Sie mit der angegebenen Näherung die Bitfehlerwahrscheinlichkeit von System $\rm (A)$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | System $\rm (A):$ $p_{\rm B} \ = \ $ { 3.5 3% } $\ \cdot 10^{-5}$ |
| − | {Welche Eigenschaften weist das System (B) auf? | + | {Welche Eigenschaften weist das System $\rm (B)$ auf? |
|type="[]"} | |type="[]"} | ||
+ Es besteht ein Phasenversatz zwischen Sender und Empfänger. | + Es besteht ein Phasenversatz zwischen Sender und Empfänger. | ||
- Das Empfangsfilter führt zu Impulsinterferenzen. | - Das Empfangsfilter führt zu Impulsinterferenzen. | ||
| − | - Es ergibt sich keine Degradation gegenüber System (A). | + | - Es ergibt sich keine Degradation gegenüber System $\rm (A)$. |
| − | { Welche Eigenschaften weist das System (C) auf? | + | { Welche Eigenschaften weist das System $\rm (C)$ auf? |
|type="[]"} | |type="[]"} | ||
- Es besteht ein Phasenversatz zwischen Sender und Empfänger. | - Es besteht ein Phasenversatz zwischen Sender und Empfänger. | ||
+ Das Empfangsfilter führt zu Impulsinterferenzen. | + Das Empfangsfilter führt zu Impulsinterferenzen. | ||
| − | - Es ergibt sich keine Degradation gegenüber System (A). | + | - Es ergibt sich keine Degradation gegenüber System $\rm (A)$. |
{ Welche Aussagen sind bezüglich den Fehlerwahrscheinlichkeiten richtig? | { Welche Aussagen sind bezüglich den Fehlerwahrscheinlichkeiten richtig? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - Alle drei Systeme weisen die gleiche Bitfehlerwahrscheinlichkeit. |
| − | + Die Fehlerwahrscheinlichkeit von System (A) ist am kleinsten. | + | + Die Fehlerwahrscheinlichkeit von System $\rm (A)$ ist am kleinsten. |
| − | + (B) besitzt eine größere | + | + Das System $\rm (B)$ besitzt eine größere Bitfehlerwahrscheinlichkeit als das System $\rm (C)$. |
| Zeile 63: | Zeile 66: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Aus der Angabe $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ folgt ${E_{\rm B}}/{N_0} = 10^{0.9}\approx 7.95 \hspace{0.05cm}.$ |
| − | + | *Mit der angegebenen Näherung gilt weiter: | |
| − | Mit der angegebenen Näherung gilt weiter: | + | :$$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \approx \frac{1}{2 \cdot\sqrt{\pi \cdot{E_{\rm B}}/{N_0}} } \cdot {\rm e}^{-{E_{\rm B}}/{N_0}} = {1}/{2 \cdot\sqrt{7.95 \cdot \pi }} \cdot {\rm e}^{-7.95}\approx \hspace{0.15cm}\underline {3.5 \cdot 10^{-5}\hspace{0.05cm}}.$$ |
| − | $$p_{\rm B} = | + | *Der exakte Wert $p_{\rm B}\hspace{0.15cm}\underline { = 3.3 · 10^{–5}}$ ist nur geringfügig kleiner. |
| − | + | ||
| − | Der exakte Wert $ | + | |
| + | |||
| + | '''(2)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | ||
| + | *Aufgrund eines Phasenversatzes um $Δϕ_{\rm T} = 30^\circ$ wurde das Phasendiagramm gedreht, was zu einer Degradation führt. | ||
| + | *Die beiden Komponenten $\rm I$ und $\rm Q$ beeinflussen sich zwar gegenseitig, es gibt aber keine Impulsinterferenzen wie bei System $\rm (C)$. | ||
| + | *Ein „Nyquistsystem” führt niemals zu Impulsinterferenzen. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| + | *Insbesondere an den jeweils neun Kreuzen in jedem Quadranten des Phasendiagramms $\rm (C)$, die den rauschfreien Fall markieren, erkennt man den Einfluss von Impulsinterferenzen. | ||
| + | *Anstelle des optimalen Empfangsfilters für rechteckförmigem Sendegrundimpuls $g_s(t)$ ⇒ rechteckförmige Impulsantwort $h_{\rm E}(t)$ wurde hier ein [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale#Gau.C3.9Fimpuls|Gaußtiefpass]] mit der (normierten) Grenzfrequenz $f_{\rm G} · T = 0.6$ verwendet. | ||
| + | *Dieser bewirkt Impulsinterferenzen. Auch ohne Rauschen gibt es in jedem Quadranten neun Kreuze, die auf je einen Vor– und Nachläufer pro Komponente hinweisen. | ||
| + | |||
| + | |||
| − | ''' | + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: |
| + | *Die Systeme $\rm (B)$ und $\rm (C)$ sind nicht optimal. Daraus ist bereits ersichtlich, dass die Aussage 1 nicht zutrifft. | ||
| + | * Dagegen ist die Aussage 2 richtig. Jedes 4–QAM–System, das dem Matched–Filter–Prinzip folgt und zusätzlich die erste Nyquistbedingung erfüllt, besitzt die vorne angegebene Fehlerwahrscheinlichkeit | ||
| + | :$$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ | ||
| + | *Die so genannte „Wurzel–Nyquist–Konfiguration”, die zum Beispiel in der Aufgabe 4.12 behandelt wurde, hat somit die genau gleiche Fehlerwahrscheinlichkeit wie das System $\rm (A)$ und zu den Detektionszeitpunkten auch das gleiche Phasendiagramm. Die Übergänge zwischen den einzelnen Punkten sind jedoch unterschiedlich. | ||
| + | *Auch die dritte Aussage ist zutreffend. Man erkennt bereits aus dem Phasendiagramm von System $\rm (B)$ Fehlentscheidungen und zwar immer dann, wenn Punkte farblich nicht zu den Quadranten passen. | ||
| − | |||
| − | + | Die Fehlerwahrscheinlichkeiten von System $\rm (B)$ und System $\rm (C)$ werden im Buch „Digitalsignalübertragung” hergeleitet. Die Ergebnisse einer Systemsimulation bestätigen die obigen Aussagen: | |
| − | : | + | * System $\rm (A)$: $p_{\rm B} ≈ 3.3 · 10^{–5}$ (siehe Teilaufgabe 1), |
| − | + | * System $\rm (B)$: $p_{\rm B} ≈ 3.5 · 10^{–2}$, | |
| − | + | * System $\rm (C)$: $p_{\rm B} ≈ 2.4 · 10^{–4}$. | |
| − | $$p_{\rm B} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 20. April 2022, 12:45 Uhr
Die Grafik $\rm (A)$ zeigt das Phasendiagramm der 4–QAM nach dem Matched–Filter, wobei eine bei AWGN–Rauschen unter der Nebenbedingung „Spitzenwertbegrenzung” optimale Realisierungsform gewählt wurde:
- rechteckförmiger Sendegrundimpuls der Symboldauer $T$,
- rechteckförmige Impulsantwort des Matched-Filters gleicher Breite $T$.
Alle hier dargestellten Phasendiagramme – sowohl $\rm (A)$ als auch $\rm (B)$ und $\rm (C)$ – beziehen sich ausschließlich auf die Detektionszeitpunkte. Die Übergänge zwischen den einzelnen zeitdiskreten Punkten sind in diesem Phasendiagrammen also nicht eingezeichnet.
- Es liegt hier ein AWGN–Kanal mit $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ vor.
- Entsprechend gilt für die Bitfehlerwahrscheinlichkeit des zunächst betrachteten Systems $\rm (A)$ :
- $$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$
Die Phasendiagramme $\rm (B)$ und $\rm (C)$ gehören zu zwei Systemen, bei denen die 4–QAM nicht optimal realisiert wurde. Auch bei diesen ist wieder jeweils AWGN–Rauschen mit $10 · \lg E_{\rm B}/N_0 = 9 \ \rm dB$ vorausgesetzt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Quadratur–Amplitudenmodulation.
- Bezug genommen wird insbesondere auf die Seite "Phasenversatz zwischen Sender und Empfänger" im Buch „Digitalsignalübertragung”.
- Die Ursachen und Auswirkungen von Impulsinterferenzen werden im gleichnamigen Abschnitt des Buches „Digitalsignalübertragung” erläutert.
- Die Kreuze in den Grafiken markieren mögliche Punkte in den Diagrammen, wenn kein AWGN–Rauschen vorhanden wäre.
- Die Punktwolken aufgrund des AWGN–Rauschens haben alle gleichen Durchmesser. Die rote Wolke erscheint nur deshalb etwas kleiner als die anderen, da „Rot” auf „Schwarz” schlechter zu erkennen ist.
- Als eine hinreichend gute Näherung für das komplementäre Gaußsche Fehlerintegral können Sie verwenden:
- $${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$
Fragebogen
Musterlösung
- Mit der angegebenen Näherung gilt weiter:
- $$p_{\rm B} = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \approx \frac{1}{2 \cdot\sqrt{\pi \cdot{E_{\rm B}}/{N_0}} } \cdot {\rm e}^{-{E_{\rm B}}/{N_0}} = {1}/{2 \cdot\sqrt{7.95 \cdot \pi }} \cdot {\rm e}^{-7.95}\approx \hspace{0.15cm}\underline {3.5 \cdot 10^{-5}\hspace{0.05cm}}.$$
- Der exakte Wert $p_{\rm B}\hspace{0.15cm}\underline { = 3.3 · 10^{–5}}$ ist nur geringfügig kleiner.
(2) Richtig ist der Lösungsvorschlag 1:
- Aufgrund eines Phasenversatzes um $Δϕ_{\rm T} = 30^\circ$ wurde das Phasendiagramm gedreht, was zu einer Degradation führt.
- Die beiden Komponenten $\rm I$ und $\rm Q$ beeinflussen sich zwar gegenseitig, es gibt aber keine Impulsinterferenzen wie bei System $\rm (C)$.
- Ein „Nyquistsystem” führt niemals zu Impulsinterferenzen.
(3) Richtig ist der Lösungsvorschlag 2:
- Insbesondere an den jeweils neun Kreuzen in jedem Quadranten des Phasendiagramms $\rm (C)$, die den rauschfreien Fall markieren, erkennt man den Einfluss von Impulsinterferenzen.
- Anstelle des optimalen Empfangsfilters für rechteckförmigem Sendegrundimpuls $g_s(t)$ ⇒ rechteckförmige Impulsantwort $h_{\rm E}(t)$ wurde hier ein Gaußtiefpass mit der (normierten) Grenzfrequenz $f_{\rm G} · T = 0.6$ verwendet.
- Dieser bewirkt Impulsinterferenzen. Auch ohne Rauschen gibt es in jedem Quadranten neun Kreuze, die auf je einen Vor– und Nachläufer pro Komponente hinweisen.
(4) Richtig sind die Lösungsvorschläge 2 und 3:
- Die Systeme $\rm (B)$ und $\rm (C)$ sind nicht optimal. Daraus ist bereits ersichtlich, dass die Aussage 1 nicht zutrifft.
- Dagegen ist die Aussage 2 richtig. Jedes 4–QAM–System, das dem Matched–Filter–Prinzip folgt und zusätzlich die erste Nyquistbedingung erfüllt, besitzt die vorne angegebene Fehlerwahrscheinlichkeit
- $$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
- Die so genannte „Wurzel–Nyquist–Konfiguration”, die zum Beispiel in der Aufgabe 4.12 behandelt wurde, hat somit die genau gleiche Fehlerwahrscheinlichkeit wie das System $\rm (A)$ und zu den Detektionszeitpunkten auch das gleiche Phasendiagramm. Die Übergänge zwischen den einzelnen Punkten sind jedoch unterschiedlich.
- Auch die dritte Aussage ist zutreffend. Man erkennt bereits aus dem Phasendiagramm von System $\rm (B)$ Fehlentscheidungen und zwar immer dann, wenn Punkte farblich nicht zu den Quadranten passen.
Die Fehlerwahrscheinlichkeiten von System $\rm (B)$ und System $\rm (C)$ werden im Buch „Digitalsignalübertragung” hergeleitet. Die Ergebnisse einer Systemsimulation bestätigen die obigen Aussagen:
- System $\rm (A)$: $p_{\rm B} ≈ 3.3 · 10^{–5}$ (siehe Teilaufgabe 1),
- System $\rm (B)$: $p_{\rm B} ≈ 3.5 · 10^{–2}$,
- System $\rm (C)$: $p_{\rm B} ≈ 2.4 · 10^{–4}$.