Aufgaben:Aufgabe 1.1Z: Redundanzfreie Binärquelle: Unterschied zwischen den Versionen
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| − | [[Datei:P_ID1257__Dig_Z_1_1.png|right|]] | + | [[Datei:P_ID1257__Dig_Z_1_1.png|right|frame|Diracförmiges Quellensignal]] |
Eine jede digitale Quelle kann durch ihre Quellensymbolfolge | Eine jede digitale Quelle kann durch ihre Quellensymbolfolge | ||
| − | $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | + | :$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ |
| − | vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit | + | vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit Null beginnt. Entstammt jedes einzelne Symbol $q_\nu$ dem Symbolvorrat $\{\rm L, \ H\}$, so spricht man von einer Binärquelle. |
| + | |||
| + | Unter Verwendung des Symbolabstandes $T$ kann man die Quellensymbolfolge $\langle q_\nu \rangle$ in äquivalenter Weise auch durch das diracförmige Quellensignal | ||
| + | :$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$ | ||
| + | kennzeichnen, was eher einer systemtheoretischen Betrachtungsweise entspricht. Hierbei bezeichnet man $a_\nu$ als die Amplitudenkoeffizienten. | ||
| + | *Im Falle einer binären unipolaren Digitalsignalübertragung gilt: | ||
| + | :$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | *Entsprechend gilt bei einem bipolaren System: | ||
| + | :$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | |||
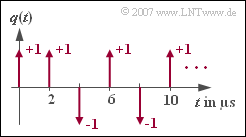
| + | In der Grafik ist das diracförmige Quellensignal $q(t)$ einer Binärquelle dargestellt. Von dieser ist bekannt, dass sie redundanzfrei ist. Diese Aussage ist für die Lösung der Aufgabe durchaus relevant. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Systemkomponenten_eines_Basisbandübertragungssystems|"Systemkomponenten eines Basisbandübertragungssystems"]]. | ||
| + | *Bezug genommen wird insbesondere auf den Abschnitt [[Digitalsignalübertragung/Systemkomponenten_eines_Basisbandübertragungssystems#Beschreibungsgr.C3.B6.C3.9Fen_der_digitalen_Quelle|"Kenngrößen der digitalen Quelle"]]. | ||
| + | *In der Literatur werden die beiden möglichen Binärsymbole meist mit $\rm L$ und $\rm 0$ bezeichnet. | ||
| + | *Um die etwas verwirrende Zuordnung $a_\nu = 1$ für $q_\nu =\rm 0$ und $a_\nu = 0$ für $q_\nu =\rm L$ zu vermeiden, werden in unserem Lerntutorial die Symbole $\rm L$ („Low”) und $\rm H$ („High”) verwendet. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| + | {Wie groß ist der Symbolabstand $T$? | ||
| + | |type="{}"} | ||
| + | $T \ = \ $ { 2 3% } $\ \rm µ s$ | ||
| − | Wie groß ist der | + | {Wie groß ist die von der Quelle abgegebene Bitrate $R$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $R \ = \ $ { 500 3% } $\ \rm kbit/s$ |
{Handelt es sich hierbei um die unipolare oder bipolare Repräsentation? | {Handelt es sich hierbei um die unipolare oder bipolare Repräsentation? | ||
| − | |type=" | + | |type="()"} |
- Die Symbolfolge ist unipolar. | - Die Symbolfolge ist unipolar. | ||
+ Die Symbolfolge ist bipolar. | + Die Symbolfolge ist bipolar. | ||
| + | {Wie lautet das Quellensymbol $q_2$? | ||
| + | |type="()"} | ||
| + | + $q_2 = \rm L$, | ||
| + | - $q_2 = \rm H$. | ||
| + | |||
| + | {Wie groß ist die Symbolwahrscheinlichkeit $p_{\rm H} = {\rm Pr}(q_\nu = \rm H$)? | ||
| + | |type="{}"} | ||
| + | $p_{\rm H} \ = \ $ { 0.5 3% } | ||
</quiz> | </quiz> | ||
| Zeile 36: | Zeile 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Entsprechend der Grafik beträgt der Abstand zweier Symbole | + | '''(1)''' Entsprechend der Grafik beträgt der Abstand zweier Symbole $\underline{T = 2\ \rm µ s}$. |
| + | |||
| + | |||
| + | '''(2)''' Bei dieser redundanzfreien Binärquelle – und nur bei einer solchen – ist die Bitrate $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$. | ||
| + | |||
| + | |||
| + | '''(3)''' Die möglichen Amplitudenkoeffizienten sind $\pm 1$. Deshalb ist die gegebene Symbolfolge <u>bipolar</u>. | ||
| − | |||
| − | + | '''(4)''' Der Amplitudenkoeffizient $a_2$ kann bei $2T = 4 \ \rm µ s$ abgelesen werden. Bei bipolarer Zuordnung folgt aus $a_2 = -1$ für das Symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$. | |
| − | |||
| − | '''( | + | '''(5)''' Auch wenn die Grafik für den hier dargestellten kurzen Zeitabschnitt etwas anderes suggeriert: |
| − | + | *Bei einer redundanzfreien Binärquelle muss neben der statistischen Unabhängigkeit der Symbole auch $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (gleichwahrscheinliche Symbole) gelten. | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 29. April 2022, 12:52 Uhr
Eine jede digitale Quelle kann durch ihre Quellensymbolfolge
- $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$
vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit Null beginnt. Entstammt jedes einzelne Symbol $q_\nu$ dem Symbolvorrat $\{\rm L, \ H\}$, so spricht man von einer Binärquelle.
Unter Verwendung des Symbolabstandes $T$ kann man die Quellensymbolfolge $\langle q_\nu \rangle$ in äquivalenter Weise auch durch das diracförmige Quellensignal
- $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$
kennzeichnen, was eher einer systemtheoretischen Betrachtungsweise entspricht. Hierbei bezeichnet man $a_\nu$ als die Amplitudenkoeffizienten.
- Im Falle einer binären unipolaren Digitalsignalübertragung gilt:
- $$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
- Entsprechend gilt bei einem bipolaren System:
- $$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
In der Grafik ist das diracförmige Quellensignal $q(t)$ einer Binärquelle dargestellt. Von dieser ist bekannt, dass sie redundanzfrei ist. Diese Aussage ist für die Lösung der Aufgabe durchaus relevant.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Systemkomponenten eines Basisbandübertragungssystems".
- Bezug genommen wird insbesondere auf den Abschnitt "Kenngrößen der digitalen Quelle".
- In der Literatur werden die beiden möglichen Binärsymbole meist mit $\rm L$ und $\rm 0$ bezeichnet.
- Um die etwas verwirrende Zuordnung $a_\nu = 1$ für $q_\nu =\rm 0$ und $a_\nu = 0$ für $q_\nu =\rm L$ zu vermeiden, werden in unserem Lerntutorial die Symbole $\rm L$ („Low”) und $\rm H$ („High”) verwendet.
Fragebogen
Musterlösung
(2) Bei dieser redundanzfreien Binärquelle – und nur bei einer solchen – ist die Bitrate $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$.
(3) Die möglichen Amplitudenkoeffizienten sind $\pm 1$. Deshalb ist die gegebene Symbolfolge bipolar.
(4) Der Amplitudenkoeffizient $a_2$ kann bei $2T = 4 \ \rm µ s$ abgelesen werden. Bei bipolarer Zuordnung folgt aus $a_2 = -1$ für das Symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$.
(5) Auch wenn die Grafik für den hier dargestellten kurzen Zeitabschnitt etwas anderes suggeriert:
- Bei einer redundanzfreien Binärquelle muss neben der statistischen Unabhängigkeit der Symbole auch $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (gleichwahrscheinliche Symbole) gelten.