Aufgaben:Aufgabe 1.2: Lognormal – Kanalmodell: Unterschied zwischen den Versionen
Tasnad (Diskussion | Beiträge) K (Textersetzung - „Komplementäre_Gaußsche_Fehlerfunktionen_(neues_Applet)“ durch „Komplementäre_Gaußsche_Fehlerfunktionen“) |
|||
| (42 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
{{quiz-Header|Buchseite=Mobile Kommunikation/Distanzabhängige Dämpfung und Abschattung | {{quiz-Header|Buchseite=Mobile Kommunikation/Distanzabhängige Dämpfung und Abschattung | ||
}} | }} | ||
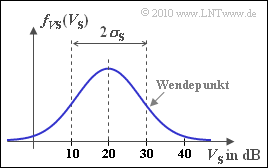
| − | [[Datei:P_ID2122__Mob_A_1_2.png|right|frame| | + | [[Datei:P_ID2122__Mob_A_1_2.png|right|frame|Wahrscheinlichkeitsdichtefunktion <br>des Lognormal–Fadings]] |
| + | Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand $d_0$ von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation. | ||
| + | |||
| + | Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar: | ||
| + | :$$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *$V_0$ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit $V_0 = 80 \ \rm dB$ als konstant angenommen wird. | ||
| + | *Der Verlust $V_{\rm S}$ ist auf Abschattungen (<i>Shadowing</i>) zurückzuführen, der durch die Lognormal–Verteilung mit folgender Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ ausreichend genau beschrieben wird (siehe Grafik): | ||
| + | :$$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) }$$ | ||
| + | |||
| + | *Beispielsweise gelten für die Teilaufgaben '''(2)''' und '''(3)''' die Zahlenwerte: | ||
| + | :$$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Gehen Sie außerdem von folgenden einfachen Annahmen aus: | ||
| + | * Die Sendeleistung beträgt $P_{\rm S} = 10 \ \rm W$ $($umgerechnet: $+40 \ \rm dBm)$. | ||
| + | * Die Empfangsleistung soll mindestens $P_{\rm E} = 10 \ \rm pW$ $($umgerechnet: $-80 \ \rm dBm)$ betragen. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Distanzabhängige Dämpfung und Abschattung]]. | ||
| + | |||
| + | * Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden: | ||
| + | :$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} | ||
| + | {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$ | ||
| + | * Oder Sie benutzen unser Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | ||
| + | |||
| Zeile 9: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wäre $P_{\rm E}$ ohne Berücksichtigung des Lognormal–Fadings ausreichend? |
| − | |type=" | + | |type="()"} |
| − | - | + | + Ja, |
| − | + | - Nein. | |
| + | {Die Lognormal–Parameter seien $m_{\rm S} = 20 \, \rm dB$ und $\sigma_{\rm S} = 0 \, \rm dB$. In wieviel Prozent der Zeit funktioniert das System? | ||
| + | |type="{}"} | ||
| + | ${\rm Pr(System \ funktioniert)} \ = \ $ { 100 3% } $\ \%$ | ||
| − | { | + | {Welche Wahrscheinlichkeit ergibt sich mit $m_{\rm S} = 20 \ \rm dB$ und $\sigma_{\rm S} = 10 \ \rm dB$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\rm Pr(System \ funktioniert)}\ = \ $ { 98 3% } $\ \%$ |
| − | |||
| − | |||
| + | {Wie groß darf $V_0$ maximal sein, damit die Zuverlässigkeit zu $99.9\%$ erreicht wird? | ||
| + | |type="{}"} | ||
| + | $V_0 \ = \ $ { 70 3% } $\ \rm dB$ | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig ist $\rm JA$: |
| − | '''2 | + | *Aus dem $\rm dB$–Wert $V_0 = 80 \ \rm dB$ folgt der absolute (lineare) Wert $K_0 = 10^8$. Damit beträgt die Empfangsleistung |
| − | ''' | + | :$$P_{\rm E} = P_{\rm S}/K_0 = 10 \ {\rm W}/10^8 = 100 \ {\rm nW} > 10 \ \rm pW.$$ |
| − | ''' | + | |
| − | ''' | + | *Man kann dieses Problem auch direkt mit den logarithmischen Größen lösen: |
| − | ''' | + | :$$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}{1\,\,{\rm mW}} = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm S}}{1\,\,{\rm mW}} - V_0 = 40\,{\rm dBm} -80\,\,{\rm dB} = -40\,\,{\rm dBm} |
| − | + | \hspace{0.05cm}.$$ | |
| + | |||
| + | *Gefordert ist aber lediglich der Grenzwert $–80 \ \rm dBm$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Lognormal–Fading mit $\sigma_{\rm S} = 0 \ \rm dB$ ist gleichbedeutend mit einer konstanten Empfangsleistung $P_{\rm E}$. | ||
| + | *Gegenüber der Teilaufgabe '''(1)''' ist diese um $m_{\rm S} = 20 \ \rm dB$ kleiner ⇒ $P_{\rm E} = \ –60 \ \rm dBm$. | ||
| + | *Sie ist aber immer noch größer als der vorgegebene Grenzwert ($-80 \ \rm dBm$). | ||
| + | *Daraus folgt: Das System ist (fast) zu <u>100% funktionsfähig</u>. | ||
| + | *„Fast” deshalb, weil es bei einer Gaußschen Zufallsgröße immer eine (kleine) Restunsicherheit gibt. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Die Empfangsleistung ist dann zu gering $($kleiner als $-80 \ \rm dBm)$, wenn der Leistungsverlust durch den Lognormal–Term $40 \ \rm dB$ oder mehr beträgt. | ||
| + | [[Datei:P_ID2187__Mob_A_1_2c_v1.png|right|frame|Verlust durch das Lognormal–Fading]] | ||
| + | *Der veränderliche Anteil $V_{\rm S}$ darf also nicht größer sein als $20 \ \rm dB$. | ||
| + | *Daraus folgt: | ||
| + | :$${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{20\,\,{\rm dB}}{\sigma_{\rm S} = 10\,{\rm dB}}\right ) $$ | ||
| + | :$$\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} {\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}(2) \approx 0.02$$ | ||
| + | :$$\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}({\rm "System\hspace{0.15cm}funktioniert"})= 1- 0.02 \hspace{0.15cm} \underline{\approx 98\,\%}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Grafik verdeutlicht das Ergebnis. | ||
| + | *Dargestellt ist hier die Wahrscheinlichkeitsdichtefunktion $f_{\rm VS}(V_{\rm S})$ des Pfadverlustes durch ''Shadowing'' (Longnormal–Fading). | ||
| + | *Die Wahrscheinlichkeit, dass das System ausfällt, ist rot markiert: | ||
| + | <br clear=all> | ||
| + | '''(4)''' Aus der Verfügbarkeitswahrscheinlichkeit $99.9 \%$ folgt die Ausfallwahrscheinlichkeit $10^{\rm –3} \approx \ {\rm Q}(3)$. | ||
| + | *Verringert man den entfernungsabhängigen Pfadverlust $V_0$ um $10 \ \rm dB$ auf $\underline {70 \ \rm dB}$, so kommt es erst dann zu einem Ausfall, wenn $V_{\rm S} ≥ 50 \ \rm dB$ ist. | ||
| + | *Damit wäre genau die geforderte Zuverlässigkeit erreicht, wie die folgende Rechnung zeigt: | ||
| + | :$${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= | ||
| + | {\rm Q}\left ( \frac{120-70-20}{10}\right ) | ||
| + | = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu | + | |
| + | |||
| + | |||
| + | [[Category:Aufgaben zu Mobile Kommunikation|^1.1 Distanzabhängige Dämpfung^]] | ||
Aktuelle Version vom 10. Juni 2020, 16:50 Uhr
Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand $d_0$ von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation.
Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar:
- $$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$
- $V_0$ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit $V_0 = 80 \ \rm dB$ als konstant angenommen wird.
- Der Verlust $V_{\rm S}$ ist auf Abschattungen (Shadowing) zurückzuführen, der durch die Lognormal–Verteilung mit folgender Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ ausreichend genau beschrieben wird (siehe Grafik):
- $$f_{V_{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm e }^{ - { (V_{\rm S}\hspace{0.05cm}- \hspace{0.05cm}m_{\rm S})^2}/(2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma_{\rm S}^2) }$$
- Beispielsweise gelten für die Teilaufgaben (2) und (3) die Zahlenwerte:
- $$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.05cm}.$$
Gehen Sie außerdem von folgenden einfachen Annahmen aus:
- Die Sendeleistung beträgt $P_{\rm S} = 10 \ \rm W$ $($umgerechnet: $+40 \ \rm dBm)$.
- Die Empfangsleistung soll mindestens $P_{\rm E} = 10 \ \rm pW$ $($umgerechnet: $-80 \ \rm dBm)$ betragen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Distanzabhängige Dämpfung und Abschattung.
- Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden:
- $${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$
- Oder Sie benutzen unser Applet Komplementäre Gaußsche Fehlerfunktionen.
Fragebogen
Musterlösung
- Aus dem $\rm dB$–Wert $V_0 = 80 \ \rm dB$ folgt der absolute (lineare) Wert $K_0 = 10^8$. Damit beträgt die Empfangsleistung
- $$P_{\rm E} = P_{\rm S}/K_0 = 10 \ {\rm W}/10^8 = 100 \ {\rm nW} > 10 \ \rm pW.$$
- Man kann dieses Problem auch direkt mit den logarithmischen Größen lösen:
- $$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}{1\,\,{\rm mW}} = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm S}}{1\,\,{\rm mW}} - V_0 = 40\,{\rm dBm} -80\,\,{\rm dB} = -40\,\,{\rm dBm} \hspace{0.05cm}.$$
- Gefordert ist aber lediglich der Grenzwert $–80 \ \rm dBm$.
(2) Lognormal–Fading mit $\sigma_{\rm S} = 0 \ \rm dB$ ist gleichbedeutend mit einer konstanten Empfangsleistung $P_{\rm E}$.
- Gegenüber der Teilaufgabe (1) ist diese um $m_{\rm S} = 20 \ \rm dB$ kleiner ⇒ $P_{\rm E} = \ –60 \ \rm dBm$.
- Sie ist aber immer noch größer als der vorgegebene Grenzwert ($-80 \ \rm dBm$).
- Daraus folgt: Das System ist (fast) zu 100% funktionsfähig.
- „Fast” deshalb, weil es bei einer Gaußschen Zufallsgröße immer eine (kleine) Restunsicherheit gibt.
(3) Die Empfangsleistung ist dann zu gering $($kleiner als $-80 \ \rm dBm)$, wenn der Leistungsverlust durch den Lognormal–Term $40 \ \rm dB$ oder mehr beträgt.
- Der veränderliche Anteil $V_{\rm S}$ darf also nicht größer sein als $20 \ \rm dB$.
- Daraus folgt:
- $${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{20\,\,{\rm dB}}{\sigma_{\rm S} = 10\,{\rm dB}}\right ) $$
- $$\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}(2) \approx 0.02$$
- $$\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}({\rm "System\hspace{0.15cm}funktioniert"})= 1- 0.02 \hspace{0.15cm} \underline{\approx 98\,\%}\hspace{0.05cm}.$$
Die Grafik verdeutlicht das Ergebnis.
- Dargestellt ist hier die Wahrscheinlichkeitsdichtefunktion $f_{\rm VS}(V_{\rm S})$ des Pfadverlustes durch Shadowing (Longnormal–Fading).
- Die Wahrscheinlichkeit, dass das System ausfällt, ist rot markiert:
(4) Aus der Verfügbarkeitswahrscheinlichkeit $99.9 \%$ folgt die Ausfallwahrscheinlichkeit $10^{\rm –3} \approx \ {\rm Q}(3)$.
- Verringert man den entfernungsabhängigen Pfadverlust $V_0$ um $10 \ \rm dB$ auf $\underline {70 \ \rm dB}$, so kommt es erst dann zu einem Ausfall, wenn $V_{\rm S} ≥ 50 \ \rm dB$ ist.
- Damit wäre genau die geforderte Zuverlässigkeit erreicht, wie die folgende Rechnung zeigt:
- $${\rm Pr}({\rm "System\hspace{0.15cm}funktioniert\hspace{0.15cm}nicht"})= {\rm Q}\left ( \frac{120-70-20}{10}\right ) = {\rm Q}(3) \approx 0.001 \hspace{0.05cm}.$$