Aufgaben:Aufgabe 1.3: Rayleigh–Fading: Unterschied zwischen den Versionen
| (44 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Mobile Kommunikation/Wahrscheinlichkeitsdichte des | + | {{quiz-Header|Buchseite=Mobile Kommunikation/Wahrscheinlichkeitsdichte des Rayleigh–Fadings}} |
| − | [[Datei:P_ID2106__Mob_A_1_3.png|right|frame]] | + | [[Datei:P_ID2106__Mob_A_1_3.png|right|frame|Zeitverlauf von Rayleigh–Fading]] |
| − | Rayleigh–Fading ist anzuwenden, wenn | + | Rayleigh–Fading ist anzuwenden, wenn |
| − | * zwischen Sender und Empfänger keine Direktverbindung gibt, und | + | * es zwischen Sender und Empfänger keine Direktverbindung gibt, und |
* das Signal den Empfänger auf vielen Wegen erreicht, aber deren Laufzeiten näherungsweise gleich sind. | * das Signal den Empfänger auf vielen Wegen erreicht, aber deren Laufzeiten näherungsweise gleich sind. | ||
| − | Ein Beispiel eines solchen Rayleigh–Kanals tritt beim Mobilfunk im städtischen Gebiet auf, wenn schmalbandige Signale verwendet werden mit Reichweiten zwischen 50 und 100 | + | Ein Beispiel eines solchen Rayleigh–Kanals tritt beim Mobilfunk im städtischen Gebiet auf, wenn schmalbandige Signale verwendet werden mit Reichweiten zwischen $50$ und $100$ Meter. |
| − | Betrachtet man die Funksignale $s(t)$ und $r(t)$ im äquivalenten Tiefpassbereich (das heißt, um die Frequenz $f = 0$ | + | Betrachtet man die Funksignale $s(t)$ und $r(t)$ im äquivalenten Tiefpassbereich $($das heißt, um die Frequenz $f = 0)$, so wird die Signalübertragung durch die Gleichung |
:$$r(t)= z(t) \cdot s(t)$$ | :$$r(t)= z(t) \cdot s(t)$$ | ||
| − | vollständig beschrieben. Die multiplikative Verfälschung | + | vollständig beschrieben. Die multiplikative Verfälschung |
:$$z(t)= x(t) + {\rm j} \cdot y(t)$$ | :$$z(t)= x(t) + {\rm j} \cdot y(t)$$ | ||
ist stets komplex und weist folgende Eigenschaften auf: | ist stets komplex und weist folgende Eigenschaften auf: | ||
| − | * Der Realteil $x(t)$ und der Imaginärteil $y(t)$ sind Gaußsche mittelwertfreie Zufallsgrößen, beide mit gleicher Varianz $\sigma^2$. Innerhalb der Komponenten $x(t)$ und $y(t)$ kann es statistische Bindungen geben, was aber für die Lösung der vorliegenden Aufgabe nicht relevant ist. Es bestehen keine Bindungen zwischen $x(t)$ und $y(t)$; deren Kreuzkorrelationsfunktion ist identisch Null. | + | * Der Realteil $x(t)$ und der Imaginärteil $y(t)$ sind Gaußsche mittelwertfreie Zufallsgrößen, beide mit gleicher Varianz $\sigma^2$. Innerhalb der Komponenten $x(t)$ und $y(t)$ kann es statistische Bindungen geben, was aber für die Lösung der vorliegenden Aufgabe nicht relevant ist. Es bestehen keine Bindungen zwischen $x(t)$ und $y(t)$; deren Kreuzkorrelationsfunktion ist identisch Null. |
| − | * Der Betrag $a(t) = |z(t)|$ besitzt eine Rayleigh–WDF, woraus sich der Name „ | + | * Der Betrag $a(t) = |z(t)|$ besitzt eine Rayleigh–WDF, woraus sich der Name „Rayleigh–Fading” ableitet: |
:$$f_a(a) = | :$$f_a(a) = | ||
| − | \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm | + | \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^ { -a^2/(2\sigma^2)} \\ |
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 | \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 | ||
| Zeile 26: | Zeile 26: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Das Betragsquadrat $p(t) = a(t)^2 = |z(t)|^2$ ist exponentialverteilt entsprechend der Gleichung | + | * Das Betragsquadrat $p(t) = a(t)^2 = |z(t)|^2$ ist exponentialverteilt entsprechend der Gleichung |
| − | :$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm | + | :$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^ { -p/(2\sigma^2)} \\ |
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 | \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 | ||
| Zeile 33: | Zeile 33: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Durch | + | Durch Messungen wurde ermittelt, dass die Zeitintervalle mit $a(t) ≤ 1$ (in der Grafik gelb hinterlegt) sich zu $\text{59 ms}$ aufaddieren (rot markierte Bereiche). Mit der Gesamtmessdauer von $\text{150 ms}$ ergibt sich so die Wahrscheinlichkeit, dass der Betrag des Rayleigh–Fadings kleiner oder gleich $1$ ist, zu |
:$${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\rm ms}}{150\,\,{\rm ms}} = 39.4 \% | :$${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\rm ms}}{150\,\,{\rm ms}} = 39.4 \% | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In der unteren Grafik grün hinterlegt ist der Wertebereich zwischen & | + | In der unteren Grafik grün hinterlegt ist der Wertebereich zwischen $\text{-3 dB}$ und $\text{+3 dB}$ hinsichtlich der logarithmierten Rayleigh–Größe $20 \cdot {\rm lg} \ a(t)$. Hierauf bezieht sich die Teilaufgabe '''(4)'''. |
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings|Wahrscheinlichkeitsdichte des Rayleigh–Fadings]] dieses Buches. | ||
| + | * Eine ähnliche Thematik wird mit anderer Herangehensweise im Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]] des Buches „Stochastische Signaltheorie” behandelt. | ||
| + | * Zur Überprüfung Ihrer Ergebnisse können Sie das interaktive Applet [[Applets:WDF,_VTF_und_Momente_spezieller_Verteilungen_(Applet)|WDF, VTF und Momente spezieller Verteilungen]] benutzen. | ||
| + | |||
| Zeile 50: | Zeile 54: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Im gesamten Bereich gilt für die Betragsfunktion | + | {Im gesamten Bereich gilt für die Betragsfunktion $a(t) ≤ 2$. Welcher Maximalwert ergibt sich in diesem Bereich für die logarithmische Größe? |
|type="{}"} | |type="{}"} | ||
| − | $Max[20 | + | ${\rm Max}\big[20 \cdot {\rm lg} \ {a(t)}\big] \ = \ $ { 6 3% } $\ \rm dB$ |
| − | {Welcher Maximalwert ergibt sich für | + | {Welcher Maximalwert ergibt sich für $p(t) = |z(t)|^2$ sowohl in linearer als auch in logarithmischer Darstellung? |
|type="{}"} | |type="{}"} | ||
| − | $Max[p(t)] \ = \ $ { 4 3% } $ | + | ${\rm Max}\big[p(t)\big] \ = \ $ { 4 3% } |
| − | + | ${\rm Max}\big[10 \cdot {\rm lg} \ p(t)\big] \ = \ $ { 6 3% } $ \ \rm dB$ | |
| − | {Es sei Pr[ | + | {Es sei ${\rm Pr}\big[a(t) ≤ 1\big] = 0.394$. Ermitteln Sie den Rayleigh–Parameter $\sigma$. |
|type="{}"} | |type="{}"} | ||
| − | $\sigma \ = \ $ { 1 3% } | + | $\sigma \ = \ $ { 1 3% } |
| − | {Mit welcher Wahrscheinlichkeit liegt die logarithmierte Rayleigh–Größe ⇒ | + | {Mit welcher Wahrscheinlichkeit liegt die logarithmierte Rayleigh–Größe ⇒ $10 \cdot {\rm lg} \ p(t)$ im Bereich zwischen zwischen $\text{-3 dB}$ und $\text{+3 dB}$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(|10 | + | ${\rm Pr}(|10 \cdot {\rm lg} \ p(t)| < 3 \ \rm dB) \ = \ $ { 0.411 3% } |
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Aus ${\rm Max}[a(t)] = 2$ folgt direkt: |
| − | :$${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm} a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} | + | :$${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''2 | + | |
| + | '''(2)''' Der Maximalwert des Betragsquadrats $p(t) = a(t)^2$ beträgt | ||
:$${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} | :$${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die logarithmische Darstellung des Betragsquadrats | + | *Die logarithmische Darstellung des Betragsquadrats $p(t)$ ist identisch mit der logarithmischen Darstellung des Betrags $a(t)$. Da $p(t)$ eine Leistungsgröße ist, gilt |
| − | :$$10 \cdot {\rm lg}\hspace{0.15cm} p(t) = 10 \cdot {\rm lg}\hspace{0.15cm} a(t)^2 = 20 \cdot {\rm lg}\hspace{0.15cm} a(t) | + | :$$10 \cdot {\rm lg}\hspace{0.15cm} p(t) = 10 \cdot {\rm lg}\hspace{0.15cm}a(t)^2 = 20 \cdot {\rm lg}\hspace{0.15cm} a(t) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Der Maximalwert ist somit ebenfalls | + | *Der Maximalwert ist somit ebenfalls $\underline{\approx 6\,\,{\rm dB}}$. |
| − | '''3 | + | |
| − | :$$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm | + | '''(3)''' Die Bedingung $a(t) ≤ 1$ ist gleichbedeutend mit der Forderung $p(t) = a(t)^2 ≤ 1$. |
| + | *Das Betragsquadrat ist bekanntermaßen exponentialverteilt, und für $p ≥ 0$ gilt demzufolge: | ||
| + | :$$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm e}^{ -p/(2\sigma^2)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | [[Datei:P_ID2112__Mob_A_1_3c.png|right|frame|WDF und Wahrscheinlichkeitsgebiete ]] | ||
| + | *Daraus folgt: | ||
| − | + | :$${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm e}^{ -p/(2\sigma^2)} \hspace{0.15cm}{\rm d}p = | |
| − | :$${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm | + | 1 - {\rm e}^{ -1/(2\sigma^2)} = 0.394$$ |
| − | 1 - {\rm | + | :$$\Rightarrow \hspace{0.3cm} {\rm e}^{ -1/(2\sigma^2)} =0.606 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
| − | :$$\Rightarrow \hspace{0.3cm} {\rm | ||
\sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
\underline{\sigma = 1} \hspace{0.05cm}.$$ | \underline{\sigma = 1} \hspace{0.05cm}.$$ | ||
| − | Die | + | Die Grafik zeigt jeweils als rot hinterlegte Fläche |
| − | + | * links die Wahrscheinlichkeit ${\rm Pr}(p(t) ≤ 1)$, | |
| − | + | * rechts die Wahrscheinlichkeit ${\rm Pr}(0.5 \le p(t) ≤ 2)$. | |
| + | |||
| + | |||
| − | '''4 | + | '''(4)''' Aus $10 \cdot {\rm lg} \ p_1 = \ –3 \ \rm dB$ folgt $p_1 = 0.5$ und die obere Grenze des Integrationsbereichs ergibt sich aus der Bedingung $10 \cdot {\rm lg} \ p_2 = +3 \ \rm dB$ zu $p_2 = 2$. |
| − | :$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm} p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = | + | *Damit erhält man gemäß der obigen Grafik: |
| − | \left [ - {\rm | + | :$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = |
| − | + | \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$ | |
| Zeile 113: | Zeile 122: | ||
| − | [[Category:Aufgaben zu | + | [[Category:Aufgaben zu Mobile Kommunikation|^1.2 WDF des Rayleigh-Fadings^]] |
Aktuelle Version vom 26. Juli 2020, 14:39 Uhr
Rayleigh–Fading ist anzuwenden, wenn
- es zwischen Sender und Empfänger keine Direktverbindung gibt, und
- das Signal den Empfänger auf vielen Wegen erreicht, aber deren Laufzeiten näherungsweise gleich sind.
Ein Beispiel eines solchen Rayleigh–Kanals tritt beim Mobilfunk im städtischen Gebiet auf, wenn schmalbandige Signale verwendet werden mit Reichweiten zwischen $50$ und $100$ Meter.
Betrachtet man die Funksignale $s(t)$ und $r(t)$ im äquivalenten Tiefpassbereich $($das heißt, um die Frequenz $f = 0)$, so wird die Signalübertragung durch die Gleichung
- $$r(t)= z(t) \cdot s(t)$$
vollständig beschrieben. Die multiplikative Verfälschung
- $$z(t)= x(t) + {\rm j} \cdot y(t)$$
ist stets komplex und weist folgende Eigenschaften auf:
- Der Realteil $x(t)$ und der Imaginärteil $y(t)$ sind Gaußsche mittelwertfreie Zufallsgrößen, beide mit gleicher Varianz $\sigma^2$. Innerhalb der Komponenten $x(t)$ und $y(t)$ kann es statistische Bindungen geben, was aber für die Lösung der vorliegenden Aufgabe nicht relevant ist. Es bestehen keine Bindungen zwischen $x(t)$ und $y(t)$; deren Kreuzkorrelationsfunktion ist identisch Null.
- Der Betrag $a(t) = |z(t)|$ besitzt eine Rayleigh–WDF, woraus sich der Name „Rayleigh–Fading” ableitet:
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^ { -a^2/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm}.$$
- Das Betragsquadrat $p(t) = a(t)^2 = |z(t)|^2$ ist exponentialverteilt entsprechend der Gleichung
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^ { -p/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} \hspace{0.05cm}.$$
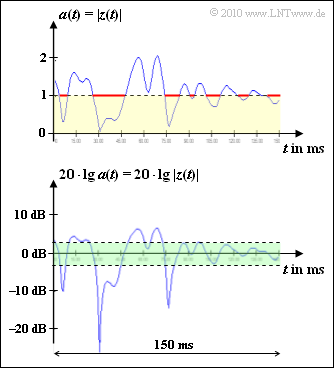
Durch Messungen wurde ermittelt, dass die Zeitintervalle mit $a(t) ≤ 1$ (in der Grafik gelb hinterlegt) sich zu $\text{59 ms}$ aufaddieren (rot markierte Bereiche). Mit der Gesamtmessdauer von $\text{150 ms}$ ergibt sich so die Wahrscheinlichkeit, dass der Betrag des Rayleigh–Fadings kleiner oder gleich $1$ ist, zu
- $${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\rm ms}}{150\,\,{\rm ms}} = 39.4 \% \hspace{0.05cm}.$$
In der unteren Grafik grün hinterlegt ist der Wertebereich zwischen $\text{-3 dB}$ und $\text{+3 dB}$ hinsichtlich der logarithmierten Rayleigh–Größe $20 \cdot {\rm lg} \ a(t)$. Hierauf bezieht sich die Teilaufgabe (4).
Hinweise:
- Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichte des Rayleigh–Fadings dieses Buches.
- Eine ähnliche Thematik wird mit anderer Herangehensweise im Kapitel Weitere Verteilungen des Buches „Stochastische Signaltheorie” behandelt.
- Zur Überprüfung Ihrer Ergebnisse können Sie das interaktive Applet WDF, VTF und Momente spezieller Verteilungen benutzen.
Fragebogen
Musterlösung
- $${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} \hspace{0.05cm}.$$
(2) Der Maximalwert des Betragsquadrats $p(t) = a(t)^2$ beträgt
- $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} \hspace{0.05cm}.$$
- Die logarithmische Darstellung des Betragsquadrats $p(t)$ ist identisch mit der logarithmischen Darstellung des Betrags $a(t)$. Da $p(t)$ eine Leistungsgröße ist, gilt
- $$10 \cdot {\rm lg}\hspace{0.15cm} p(t) = 10 \cdot {\rm lg}\hspace{0.15cm}a(t)^2 = 20 \cdot {\rm lg}\hspace{0.15cm} a(t) \hspace{0.05cm}.$$
- Der Maximalwert ist somit ebenfalls $\underline{\approx 6\,\,{\rm dB}}$.
(3) Die Bedingung $a(t) ≤ 1$ ist gleichbedeutend mit der Forderung $p(t) = a(t)^2 ≤ 1$.
- Das Betragsquadrat ist bekanntermaßen exponentialverteilt, und für $p ≥ 0$ gilt demzufolge:
- $$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm e}^{ -p/(2\sigma^2)} \hspace{0.05cm}.$$
- Daraus folgt:
- $${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm e}^{ -p/(2\sigma^2)} \hspace{0.15cm}{\rm d}p = 1 - {\rm e}^{ -1/(2\sigma^2)} = 0.394$$
- $$\Rightarrow \hspace{0.3cm} {\rm e}^{ -1/(2\sigma^2)} =0.606 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{\sigma = 1} \hspace{0.05cm}.$$
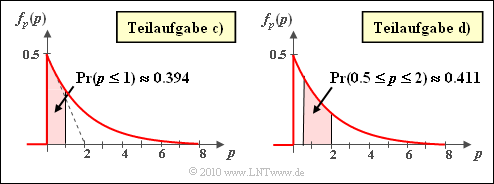
Die Grafik zeigt jeweils als rot hinterlegte Fläche
- links die Wahrscheinlichkeit ${\rm Pr}(p(t) ≤ 1)$,
- rechts die Wahrscheinlichkeit ${\rm Pr}(0.5 \le p(t) ≤ 2)$.
(4) Aus $10 \cdot {\rm lg} \ p_1 = \ –3 \ \rm dB$ folgt $p_1 = 0.5$ und die obere Grenze des Integrationsbereichs ergibt sich aus der Bedingung $10 \cdot {\rm lg} \ p_2 = +3 \ \rm dB$ zu $p_2 = 2$.
- Damit erhält man gemäß der obigen Grafik:
- $${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$