Aufgaben:Aufgabe 1.6: AKF und LDS bei Rice–Fading: Unterschied zwischen den Versionen
| (32 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Nichtfrequenzselektives Fading mit Direktkomponente}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Nichtfrequenzselektives Fading mit Direktkomponente}} | ||
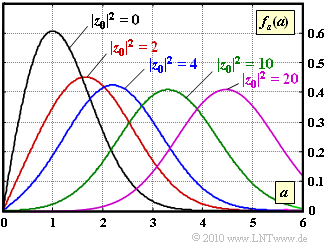
| − | [[Datei:P_ID2132__Mob_A_1_6.png|right|frame]] | + | [[Datei:P_ID2132__Mob_A_1_6.png|right|frame|Rice-WDF für verschiedene Werte von $z_0^2$]] |
| − | Man spricht | + | Man spricht von <i>Rice–Fading</i>, wenn der den Mobilfunkkanal beschreibende komplexe Faktor $z(t)$ neben der rein stochastischen Komponente $x(t) +{\rm j} \cdot y(t)$ zusätzlich einen deterministischen Anteil der Form $x_0 + {\rm j} \cdot y_0$ besitzt. |
| + | |||
Die Gleichungen des Rice–Fadings lassen sich in aller Kürze wie folgt zusammenfassen: | Die Gleichungen des Rice–Fadings lassen sich in aller Kürze wie folgt zusammenfassen: | ||
:$$r(t) = z(t) \cdot s(t) ,$$ | :$$r(t) = z(t) \cdot s(t) ,$$ | ||
| Zeile 11: | Zeile 12: | ||
Dabei gilt: | Dabei gilt: | ||
| − | * Der direkte Pfad wird durch die komplexe Konstante $z_0 = x_0 + j \cdot y_0$ beschrieben. Der Betrag dieser zeitinvarianten Komponente ist | + | * Der direkte Pfad wird durch die komplexe Konstante $z_0 = x_0 + {\rm j} \cdot y_0$ beschrieben. Der Betrag dieser zeitinvarianten Komponente ist |
:$$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$ | :$$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$ | ||
| − | * $u(t)$ und $ | + | * $u(t)$ und $v(t)$ sind Musterfunktionen mittelwertfreier Gaußscher Zufallsprozesse, beide mit Varianz $\sigma^2$ und miteinander nicht korreliert. Sie berücksichtigen Streu–, Brechungs– und Beugungseffekte auf einer Vielzahl von indirekten Pfaden. |
| − | * Der Betrag $a(t) = |z(t)|$ besitzt eine Rice–WDF, eine Eigenschaft, die für die Namensgebung dieses speziellen Mobilfunkkanals verantwortlich ist. Die WDF–Gleichung lautet für $a ≥ 0$: | + | * Der Betrag $a(t) = |z(t)|$ besitzt eine Rice–WDF, eine Eigenschaft, die für die Namensgebung dieses speziellen Mobilfunkkanals verantwortlich ist. Die WDF–Gleichung lautet für $a ≥ 0$: |
:$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = | :$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = | ||
\sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Grafik zeigt die Rice–WDF für $|z_0|^2 = 0, 2, 4, 10$ und $20$. Für alle Kurven gilt $\sigma = 1 ⇒ \sigma^2 = 1$. | + | Die Grafik zeigt die Rice–WDF für $|z_0|^2 = 0,\ 2, \ 4, \ 10$ und $20$. Für alle Kurven gilt $\sigma = 1$ ⇒ $\sigma^2 = 1$. |
| − | In dieser Aufgabe betrachten wir aber nicht die WDF des Betrags, sondern die AKF des komplexen Faktors $z(t)$, | + | |
| − | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\ | + | |
| + | In dieser Aufgabe betrachten wir aber nicht die WDF des Betrags, sondern die Autokorrelationsfunktion $\rm (AKF)$ des komplexen Faktors $z(t)$, | ||
| + | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | sowie das dazugehörige Leistungsdichtespektrum | + | sowie das dazugehörige Leistungsdichtespektrum $\rm (LDS)$ |
:$${\it \Phi}_z (f_{\rm D}) | :$${\it \Phi}_z (f_{\rm D}) | ||
\hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) | \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) | ||
| Zeile 30: | Zeile 33: | ||
| − | '' | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Nichtfrequenzselektives_Fading_mit_Direktkomponente|Nichtfrequenzselektives Fading mit Direktkomponente]]. | ||
| + | * Bezug genommen wird auch auf die Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion (AKF)]] und [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum (LDS)]] im Buch „Stochastische Signaltheorie”. | ||
| + | |||
| Zeile 37: | Zeile 50: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welcher $|z_0|^2$–Wert beschreibt das Rayleigh–Fading? | + | {Welcher $|z_0|^2$–Wert beschreibt das Rayleigh–Fading? |
|type="{}"} | |type="{}"} | ||
| − | $|z_0|^2 \ = \ $ { 0. | + | $|z_0|^2 \ = \ $ { 0. } $\ \rm $ |
| − | {Welche der folgenden Größen hängen nur von $|z_0|^2 | + | {Es gelte $|z_0|^2 \ne 0$. Welche der folgenden Größen hängen nur von $|z_0|^2 = x_0^2$ + $y_0^2$ ab, nicht aber von dessen Komponenten $x_0^2$ und $y_0^2$ allein? |
|type="[]"} | |type="[]"} | ||
| − | - WDF $f_x(x)$ des Realteils, | + | - WDF $f_x(x)$ des Realteils, |
| − | - WDF $f_y(y)$ des Imaginärteils, | + | - WDF $f_y(y)$ des Imaginärteils, |
| − | + WDF $f_a(a)$ des Betrags, | + | + WDF $f_a(a)$ des Betrags, |
| − | - WDF $f_{\rm \phi}(\phi)$ der Phase, | + | - WDF $f_{\rm \phi}(\phi)$ der Phase, |
| − | + AKF $\varphi_z(\Delta t)$ der komplexen Größe $z(t)$, | + | + AKF $\varphi_z(\Delta t)$ der komplexen Größe $z(t)$, |
| − | + LDS $\ | + | + LDS ${\it \Phi}_z(f_{\rm D})$ der komplexen Größe $z(t)$. |
| − | {Berechnen Sie den quadratischen | + | {Berechnen Sie den quadratischen Erwartungswert ${\rm E}\big[|z(t)|^2\big]$ für verschiedene Werte von $|z_0|^2$. Es gelte $\sigma^2 = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $|z_0|^2 = 0: E[|z(t)|^2] \ = \ $ { 2 3% } $\ \rm $ | + | $|z_0|^2 = 0\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 2 3% } $\ \rm $ |
| − | $|z_0|^2 = 2: E[|z(t)|^2] \ = \ $ { 4 3% } $\ \rm $ | + | $|z_0|^2 = 2\text{:} \hspace{0.52cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 4 3% } $\ \rm $ |
| − | $|z_0|^2 = 10: E[|z(t)|^2] \ = \ $ { 12 3% } $\ \rm $ | + | $|z_0|^2 = 10\text{:} \hspace{0.3cm} {\rm E}\big[|z(t)|^2\big] \ = \ $ { 12 3% } $\ \rm $ |
| − | {Wie unterscheiden sich die Autokorrelationsfunktionen (kurz: AKF) des schwarzen, des blauen und des grünen Kanals? | + | {Wie unterscheiden sich die Autokorrelationsfunktionen (kurz: AKF) des schwarzen, des blauen und des grünen Kanals? |
|type="[]"} | |type="[]"} | ||
| − | + Die „blaue” AKF liegt um 4 über der „schwarzen”. | + | + Die „blaue” AKF liegt um den Wert $4$ über der „schwarzen”. |
| − | - Die „blaue” AKF liegt um 2 unterhalb der „schwarzen”. | + | - Die „blaue” AKF liegt um den Wert $2$ unterhalb der „schwarzen”. |
| − | - Die „grüne” AKF ist um den Faktor 2.5 breiter als die „blaue”. | + | - Die „grüne” AKF ist um den Faktor $2.5$ breiter als die „blaue”. |
| − | {Wie unterscheiden sich die Leistungsdichtespektren (kurz: LDS) von schwarzem, blauem und grünem Mobilfunkkanal? | + | {Wie unterscheiden sich die Leistungsdichtespektren (kurz: LDS) von schwarzem, blauem und grünem Mobilfunkkanal? |
|type="[]"} | |type="[]"} | ||
+ Das „schwarze” LDS ist rein kontinuierlich (kein Dirac). | + Das „schwarze” LDS ist rein kontinuierlich (kein Dirac). | ||
| Zeile 71: | Zeile 84: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Das <i>Rayleigh–Fading</i> ergibt sich aus dem <i>Rice–Fading</i> mit $|z_0|^2 \ \underline {= \ 0}$. |
| + | |||
| + | '''(2)''' Richtig sind die <u>Lösungsvorschläge 3, 5 und 6</u>: | ||
| − | + | Es ist offensichtlich, dass | |
| − | * $f_x(x)$ von $x_0$ abhängt, | + | * $f_x(x)$ von $x_0$ abhängt, |
| − | * $f_y(y)$ von $y_0$ abhängt, | + | * $f_y(y)$ von $y_0$ abhängt, |
| − | * $f_{\rm \phi}(\phi)$ vom Verhältnis $y_0/x_0$ abhängt. | + | * $f_{\rm \phi}(\phi)$ vom Verhältnis $y_0/x_0$ abhängt. |
| − | Die angegebene Gleichung für die WDF $f_a(a)$ zeigt, dass der Betrag $a$ nur von $|z_0|$ abhängt. | + | Die angegebene Gleichung für die WDF $f_a(a)$ zeigt, dass der Betrag $a$ nur von $|z_0|$ abhängt. |
| − | Für die AKF gilt mit $z(t) = x(t) + j \cdot y(t)$: | + | *Für die AKF gilt mit $z(t) = x(t) + {\rm j} \cdot y(t)$: |
| − | :$$\varphi_z ({\rm \Delta}t) | + | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right] = {\rm E}\left [ \left ( x(t) + {\rm j} \cdot y(t) \right )\cdot (x(t + {\rm \Delta}t) - {\rm j} \cdot (y(t+ {\rm \Delta}t)\right ] |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Aufgrund der statistischen Unabhängigkeit zwischen Real– und Imaginärteil kann man die Gleichung wie folgt vereinfachen: | + | *Aufgrund der statistischen Unabhängigkeit zwischen Real– und Imaginärteil kann man die Gleichung wie folgt vereinfachen: |
:$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + | :$$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + | ||
{\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$ | {\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$ | ||
| − | Der erste Anteil ergibt mit $x(t) = u(t) + x_0$ und $t' = t + \Delta t$: | + | *Der erste Anteil ergibt mit $x(t) = u(t) + x_0$ und $t' = t + \Delta t$: |
:$${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] | :$${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] | ||
+ x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$ | + x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$ | ||
| Zeile 97: | Zeile 111: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei ist berücksichtigt, dass die Gaußsche Zufallsgröße $u(t)$ mittelwertfrei ist und die Varianz $\sigma^2$ besitzt. | + | *Hierbei ist berücksichtigt, dass die Gaußsche Zufallsgröße $u(t)$ mittelwertfrei ist und die Varianz $\sigma^2$ besitzt. |
| − | In gleicher Weise erhält man mit $y(t) = \upsilon (t) + y_0$: | + | |
| − | :$${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = ... = \varphi_v ({\rm \Delta}t) + y_0^2 | + | *In gleicher Weise erhält man mit $y(t) = \upsilon (t) + y_0$: |
| − | + | :$${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = \ ... \ = \varphi_v ({\rm \Delta}t) + y_0^2 \hspace{0.3cm} | |
| + | \Rightarrow \hspace{0.3cm} \varphi_z ({\rm \Delta}t) = \varphi_u ({\rm \Delta}t) + \varphi_v ({\rm \Delta}t) + x_0^2 + y_0^2 | ||
= 2 \cdot \varphi_u ({\rm \Delta}t) + |z_0|^2 | = 2 \cdot \varphi_u ({\rm \Delta}t) + |z_0|^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Wenn aber die AKF $\ | + | *Wenn aber die AKF $\varphi_z(\Delta t)$ nur von $|z_0^2|$ abhängt, dann gilt dies auch für die Fouriertransformierte „LDS”. |
| − | '''3 | + | |
| − | :$${\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a | + | '''(3)''' Der quadratische Erwartungswert, also das "Moment zweiter Ordnung", könnte zum Beispiel aus der Betrags–WDF berechnet werden: |
| + | :$$m_2 = {\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Gleichzeitig ist | + | *Gleichzeitig ist das Moment $m_2$ – also die Leistung – auch durch die AKF bestimmt: |
:$${\rm E}\left [ |z(t)|^2 \right ] = \varphi_z ({\rm \Delta}t = 0) = 2 \cdot \varphi_u ({\rm \Delta}t = 0) + |z_0|^2 = 2 \cdot \sigma^2 + |z_0|^2 | :$${\rm E}\left [ |z(t)|^2 \right ] = \varphi_z ({\rm \Delta}t = 0) = 2 \cdot \varphi_u ({\rm \Delta}t = 0) + |z_0|^2 = 2 \cdot \sigma^2 + |z_0|^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Mit $\ | + | *Mit $\sigma = 1$ erhält man somit folgende numerische Ergebnisse: |
| − | :$$ |z_0|^2 = 0 \ | + | :$$ \ \ |z_0|^2 = 0\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 0 \hspace{0.15cm} \underline{ = 2} \hspace{0.05cm},$$ |
| − | :$$ |z_0|^2 = 2 \ | + | :$$ \ \ |z_0|^2 = 2\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 2 \hspace{0.15cm} \underline{ = 4} \hspace{0.05cm},$$ |
| − | :$$|z_0|^2 = 10 \ | + | :$$\ \ |z_0|^2 = 10\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 10 \hspace{0.15cm} \underline{ = 12} \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | '''(4)''' Richtig ist der <u>Lösungsvorschlag 1</u>, wie bereits in der Musterlösung zu '''(2)''' hergeleitet wurde. | ||
| + | Richtig wären auch die folgenden Aussagen: | ||
| + | * Die „blaue” AKF liegt um 4 über der „schwarzen”. | ||
| + | * Die „grüne” AKF liegt um 6 über der „blauen”. | ||
| − | |||
| − | '''5 | + | '''(5)''' <u>Alle Lösungsvorschläge treffen zu</u>. |
| + | * Das „schwarze” LDS ist ein [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading|Jakes–Spektrum]] und damit auch kontinuierlich, das heißt, innerhalb eines Intervalls sind alle Frequenzen vorhanden. | ||
| + | * In der Autokorrelationsfunktion (AKF) des blauen bzw. des grünen Kanals tritt zusätzlich die Konstante $|z_0|^2$ auf. | ||
| + | * Im Leistungsdichtespektrum (LDS) gibt es wegen dieser Konstanten in der AKF jeweils Diracfunktionen bei der Dopplerfrequenz $f_{\rm D} = 0$ mit dem Gewicht $|z_0|^2$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu | + | [[Category:Aufgaben zu Mobile Kommunikation|^1.4 Fading mit Direktkomponente^]] |
Aktuelle Version vom 17. Februar 2022, 14:51 Uhr
Man spricht von Rice–Fading, wenn der den Mobilfunkkanal beschreibende komplexe Faktor $z(t)$ neben der rein stochastischen Komponente $x(t) +{\rm j} \cdot y(t)$ zusätzlich einen deterministischen Anteil der Form $x_0 + {\rm j} \cdot y_0$ besitzt.
Die Gleichungen des Rice–Fadings lassen sich in aller Kürze wie folgt zusammenfassen:
- $$r(t) = z(t) \cdot s(t) ,$$
- $$z(t) = x(t) + {\rm j} \cdot y(t) ,$$
- $$x(t) = u(t) + x_0 ,$$
- $$y(t) = v(t) + y_0 .$$
Dabei gilt:
- Der direkte Pfad wird durch die komplexe Konstante $z_0 = x_0 + {\rm j} \cdot y_0$ beschrieben. Der Betrag dieser zeitinvarianten Komponente ist
- $$|z_0| = \sqrt{x_0^2 + y_0^2}\hspace{0.05cm}.$$
- $u(t)$ und $v(t)$ sind Musterfunktionen mittelwertfreier Gaußscher Zufallsprozesse, beide mit Varianz $\sigma^2$ und miteinander nicht korreliert. Sie berücksichtigen Streu–, Brechungs– und Beugungseffekte auf einer Vielzahl von indirekten Pfaden.
- Der Betrag $a(t) = |z(t)|$ besitzt eine Rice–WDF, eine Eigenschaft, die für die Namensgebung dieses speziellen Mobilfunkkanals verantwortlich ist. Die WDF–Gleichung lautet für $a ≥ 0$:
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.2cm}{\rm I }_0 (u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.$$
Die Grafik zeigt die Rice–WDF für $|z_0|^2 = 0,\ 2, \ 4, \ 10$ und $20$. Für alle Kurven gilt $\sigma = 1$ ⇒ $\sigma^2 = 1$.
In dieser Aufgabe betrachten wir aber nicht die WDF des Betrags, sondern die Autokorrelationsfunktion $\rm (AKF)$ des komplexen Faktors $z(t)$,
- $$\varphi_z ({\rm \Delta}t) = {\rm E}\big [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\big ] \hspace{0.05cm},$$
sowie das dazugehörige Leistungsdichtespektrum $\rm (LDS)$
- $${\it \Phi}_z (f_{\rm D}) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.3cm} \varphi_z ({\rm \Delta}t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Nichtfrequenzselektives Fading mit Direktkomponente.
- Bezug genommen wird auch auf die Kapitel Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) im Buch „Stochastische Signaltheorie”.
Fragebogen
Musterlösung
(2) Richtig sind die Lösungsvorschläge 3, 5 und 6:
Es ist offensichtlich, dass
- $f_x(x)$ von $x_0$ abhängt,
- $f_y(y)$ von $y_0$ abhängt,
- $f_{\rm \phi}(\phi)$ vom Verhältnis $y_0/x_0$ abhängt.
Die angegebene Gleichung für die WDF $f_a(a)$ zeigt, dass der Betrag $a$ nur von $|z_0|$ abhängt.
- Für die AKF gilt mit $z(t) = x(t) + {\rm j} \cdot y(t)$:
- $$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ z(t) \cdot z^{\star}(t + {\rm \Delta}t)\right] = {\rm E}\left [ \left ( x(t) + {\rm j} \cdot y(t) \right )\cdot (x(t + {\rm \Delta}t) - {\rm j} \cdot (y(t+ {\rm \Delta}t)\right ] \hspace{0.05cm}.$$
- Aufgrund der statistischen Unabhängigkeit zwischen Real– und Imaginärteil kann man die Gleichung wie folgt vereinfachen:
- $$\varphi_z ({\rm \Delta}t) = {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] + {\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] \hspace{0.05cm}.$$
- Der erste Anteil ergibt mit $x(t) = u(t) + x_0$ und $t' = t + \Delta t$:
- $${\rm E}\left [ x(t) \cdot x(t')\right ] = {\rm E}\left [ u(t) \cdot u(t')\right ] + x_0 \cdot {\rm E}\left [ u(t) \right ] + x_0 \cdot {\rm E}\left [ u(t') \right ] + x_0^2\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm} {\rm E}\left [ x(t) \cdot x(t + {\rm \Delta}t)\right ] = {\rm E}\left [ u(t) \cdot u(t + {\rm \Delta}t)\right ] + x_0^2 = \varphi_u ({\rm \Delta}t) + x_0^2 \hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass die Gaußsche Zufallsgröße $u(t)$ mittelwertfrei ist und die Varianz $\sigma^2$ besitzt.
- In gleicher Weise erhält man mit $y(t) = \upsilon (t) + y_0$:
- $${\rm E}\left [ y(t) \cdot y(t + {\rm \Delta}t)\right ] = \ ... \ = \varphi_v ({\rm \Delta}t) + y_0^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_z ({\rm \Delta}t) = \varphi_u ({\rm \Delta}t) + \varphi_v ({\rm \Delta}t) + x_0^2 + y_0^2 = 2 \cdot \varphi_u ({\rm \Delta}t) + |z_0|^2 \hspace{0.05cm}.$$
- Wenn aber die AKF $\varphi_z(\Delta t)$ nur von $|z_0^2|$ abhängt, dann gilt dies auch für die Fouriertransformierte „LDS”.
(3) Der quadratische Erwartungswert, also das "Moment zweiter Ordnung", könnte zum Beispiel aus der Betrags–WDF berechnet werden:
- $$m_2 = {\rm E}\left [ |z(t)|^2 \right ] = {\rm E}\left [ a^2 \right ] = \int_{0}^{\infty}a^2 \cdot f_a(a)\hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$
- Gleichzeitig ist das Moment $m_2$ – also die Leistung – auch durch die AKF bestimmt:
- $${\rm E}\left [ |z(t)|^2 \right ] = \varphi_z ({\rm \Delta}t = 0) = 2 \cdot \varphi_u ({\rm \Delta}t = 0) + |z_0|^2 = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$
- Mit $\sigma = 1$ erhält man somit folgende numerische Ergebnisse:
- $$ \ \ |z_0|^2 = 0\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 0 \hspace{0.15cm} \underline{ = 2} \hspace{0.05cm},$$
- $$ \ \ |z_0|^2 = 2\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 2 \hspace{0.15cm} \underline{ = 4} \hspace{0.05cm},$$
- $$\ \ |z_0|^2 = 10\text{:} \ \hspace{0.3cm}{\rm E}\left [ |z(t)|^2 \right ] = 2 + 10 \hspace{0.15cm} \underline{ = 12} \hspace{0.05cm}.$$
(4) Richtig ist der Lösungsvorschlag 1, wie bereits in der Musterlösung zu (2) hergeleitet wurde.
Richtig wären auch die folgenden Aussagen:
- Die „blaue” AKF liegt um 4 über der „schwarzen”.
- Die „grüne” AKF liegt um 6 über der „blauen”.
(5) Alle Lösungsvorschläge treffen zu.
- Das „schwarze” LDS ist ein Jakes–Spektrum und damit auch kontinuierlich, das heißt, innerhalb eines Intervalls sind alle Frequenzen vorhanden.
- In der Autokorrelationsfunktion (AKF) des blauen bzw. des grünen Kanals tritt zusätzlich die Konstante $|z_0|^2$ auf.
- Im Leistungsdichtespektrum (LDS) gibt es wegen dieser Konstanten in der AKF jeweils Diracfunktionen bei der Dopplerfrequenz $f_{\rm D} = 0$ mit dem Gewicht $|z_0|^2$.