Aufgaben:Aufgabe 1.3Z: Schwellenwertoptimierung: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| − | [[Datei: | + | [[Datei:P_ID1268__Dig_Z_1_3.png|right|frame|Zur Optimierung des Schwellenwertes]] |
| − | + | In dieser Aufgabe wird ein bipolares Binärsystem mit AWGN–Rauschen ("Additive White Gaussian Noise") betrachtet, so dass für die Bitfehlerwahrscheinlichkeit gilt: | |
| − | + | :$$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= {1}/{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2} \cdot \sigma_d}\right) \hspace{0.05cm}.$$ | |
| − | + | Hierbei sind folgende Funktionen verwendet: | |
| − | + | :$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | |
| − | + | x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} | |
| − | $$ | + | \hspace{0.05cm},\hspace{1cm}{\rm erfc} ({\it x}) = \frac{\rm 2}{\sqrt{\rm |
| − | + | \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | |
| + | \hspace{0.05cm}.$$ | ||
| + | *Die obige Gleichung gilt für den Schwellenwert $E = 0$ unabhängig von den Symbolwahrscheinlichkeiten $p_{\rm L}$ und $p_{\rm H}$. | ||
| + | *Allerdings kann mit einem anderen Schwellenwert $E$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden, wenn die beiden Auftrittswahrscheinlichkeiten unterschiedlich sind $(p_{\rm L} ≠ p_{\rm H})$. | ||
| − | |||
| + | Die Streuung des Rauschanteils ist stets $σ_{d} = 0.5 \ \rm V$. Die beiden Amplituden des Detektionsnutzanteils sind mit $±1 \ \rm V$ fest vorgegeben. | ||
| − | + | Zu untersuchen sind folgende Symbolwahrscheinlichkeiten: | |
| − | $$ | + | *$p_{\rm L} = 0.88$ ⇒ $p_{\rm H} = 1- p_{\rm L} =0.12$, |
| − | + | *$p_{\rm L} = 0.31$ ⇒ $p_{\rm H} = 1- p_{\rm L} =0.69$. | |
| − | \hspace{0. | + | |
| − | + | ||
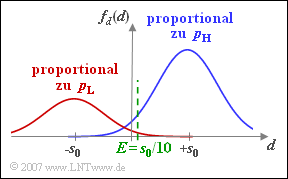
| − | + | In der Grafik ist dieser letzte Parametersatz und der Schwellenwert $E =s_{\rm 0}/10$ berücksichtigt. Dargestellt ist die Wahrscheinlichkeitsdichtefunktion $\rm WDF$ der Detektionsabtastwerte $d$. | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung|"Fehlerwahrscheinlichkeit bei Basisbandübertragung"]]. | ||
| + | |||
| + | *Zur Bestimmung von Fehlerwahrscheinlichkeiten können Sie das interaktive Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Komplementäre Gaußsche Fehlerfunktionen"]] verwenden. | ||
| + | |||
| + | *Für die Ableitung der Q–Funktion gilt: | ||
| + | :$$\frac{{\rm d\hspace{0.05cm}Q} ({\it x})} {{\rm d}\hspace{0.05cm}x} = \frac{\rm 1}{\sqrt{\rm 2\pi}} | ||
| + | \cdot \rm e^{\it -x^{\rm 2}/\rm 2} \hspace{0.05cm}.$$ | ||
| Zeile 27: | Zeile 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welcher Zusammenhang besteht zwischen den Funktionen ${\rm Q}(x)$ und ${\rm erfc}(x)$? |
| − | |type=" | + | |type="()"} |
| − | - | + | +${\rm erfc}(x) =2 \cdot {\rm Q}(\sqrt{2} \cdot x)$, |
| − | + | -${\rm erfc}(x) =\sqrt{2} \cdot {\rm Q}(x/\sqrt{2})$, | |
| + | -${\rm erfc}(x) \approx {\rm Q}(x)$. | ||
| − | { | + | {Welche Bitfehlerwahrscheinlichkeit ergibt sich mit $\underline{p_{\rm L} = 0.88}$ und $\underline{E = 0}$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $p_{\rm B} \ =\ $ { 2,27 3% } $\ \%$ |
| + | {Welche Bitfehlerwahrscheinlichkeit ergibt sich mit $p_{\rm L} = 0.88$ und $\underline{E = 0.1 \hspace{0.05cm} \rm V}$? | ||
| + | |type="{}"} | ||
| + | $p_{\rm B} \ =\ $ { 1,65 3% } $\ \%$ | ||
| + | |||
| + | {Bestimmen Sie den optimalen Schwellenwert $E_{\rm opt}$ für $p_{\rm L} = 0.88$ ⇒ $p_{\rm H} = 0.12$. | ||
| + | |type="{}"} | ||
| + | $E_{\rm opt} \ =\ $ { 0.25 3% } $\ \rm V$ | ||
| + | {Es gelte $E = E_{\rm opt}$. Wie groß ist die minimale Bitfehlerwahrscheinlichkeit mit $p_{\rm L} = 0.88$? | ||
| + | |type="{}"} | ||
| + | $p_{\rm B,\ min} \ =\ $ { 1.35 3% } $\ \%$ | ||
| + | |||
| + | {Bestimmen Sie den optimalen Schwellenwert $E_{\rm opt}$ für $\underline{p_{\rm L} = 0.31}$ ⇒ $p_{\rm H} = 0.69$. | ||
| + | |type="{}"} | ||
| + | $E_{\rm opt} \ =\ $ { -0.103--0.097 } $\ \rm V$ | ||
| + | |||
| + | {Wie groß ist die minimale Bitfehlerwahrscheinlichkeit für diesen Fall $(p_{\rm L} = 0.31)$? | ||
| + | |type="{}"} | ||
| + | $p_{\rm B,\ min} \ =\ $ { 2.07 3% } $\ \%$ | ||
</quiz> | </quiz> | ||
| Zeile 43: | Zeile 78: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Aus der Q–Funktion ergibt sich mit der Substitution $t^{2} = u^{2}/2$: |
| − | '''(2)''' | + | :$$\rm Q (\it x)= \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it |
| − | '''(3)''' | + | x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u = |
| − | '''(4)''' | + | \frac{\rm 1}{\sqrt{\rm \pi}}\int_{\it |
| − | '''(5)''' | + | x/\sqrt{\rm 2}}^{+\infty}\rm e^{\it -t^{\hspace{0.05cm}\rm 2}}\,{d \it t} = |
| − | '''(6)''' | + | {1}/{2} \cdot {\rm erfc} \left( {x}/{\sqrt{2}} |
| + | \right)\hspace{0.05cm}.$$ | ||
| + | Daraus folgt die Richtigkeit des <u>ersten Lösungsvorschlags</u>: | ||
| + | :$${\rm erfc} (x)= 2 \cdot {\rm Q} (\sqrt{2} \cdot x) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Unabhängig von den Symbolwahrscheinlichkeiten erhält man mit der Entscheiderschwelle $E = 0$: | ||
| + | :$$p_{\rm B} = {\rm Q} \left( {s_0}/{\sigma_d}\right)= {\rm Q} (2) \hspace{0.1cm}\underline {= 2.27 \, \% }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Nun lautet die allgemeine Gleichung für die Bitfehlerwahrscheinlichkeit, wobei $d_{\rm N}$ den Rauschanteil von $d(t)$ bezeichnet: | ||
| + | :$$p_{\rm B} \ = \ p_{\rm L} \cdot {\rm Pr}( d_{\rm N}> E + s_0)+ | ||
| + | p_{\rm H} \cdot {\rm Pr}( d_{\rm N}< E - s_0) \ = \ p_{\rm L} \cdot {\rm Q} \left( \frac{s_0 + E}{\sigma_d}\right)+ | ||
| + | p_{\rm H} \cdot {\rm Q} \left( \frac{s_0 - E}{\sigma_d}\right)\hspace{0.05cm}.$$ | ||
| + | *Hierbei ist die WDF-Symmetrie berücksichtigt. Mit $p_{\rm L} = 0.88$ ⇒ $p_{\rm H} = 0.12$ und $E = 0.1 \hspace{0.05cm} \rm V $ erhält man: | ||
| + | :$$p_{\rm B} \hspace{-0.05cm}=\hspace{-0.05cm} 0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{\rm Q} \left( \frac{1\, {\rm V} + 0.1\, {\rm V}}{0.5\, {\rm V}}\right)\hspace{-0.05cm}+\hspace{-0.05cm} | ||
| + | 0.12 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{\rm Q} \left( \frac{1\, {\rm V} - 0.1\, {\rm V}}{0.5\, {\rm V}}\right) \hspace{-0.05cm}=\hspace{-0.05cm} 0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm} {\rm Q}(2.2) \hspace{-0.05cm}+\hspace{-0.05cm} 0.12 \cdot {\rm Q}(1.8) \hspace{-0.05cm}= \hspace{-0.05cm}0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm} 1.39\,\% \hspace{-0.05cm}+\hspace{-0.05cm} 0.12 \hspace{-0.03cm}\cdot \hspace{-0.03cm} 3.59\,\%\ \hspace{0.1cm}\underline { = 1.65\,\% } \hspace{0.05cm}.$$ | ||
| + | *Durch die Schwellenverschiebung nach rechts um $E = s_{0}/10$ ergibt sich eine Verbesserung von $p_{\rm B} = 2.27 \ \%$ auf $p_{\rm B} = 1.65 \ \%$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Diese Optimierungsaufgabe wird durch Nullsetzen der Ableitung gelöst, wobei der Hinweis auf der Angabenseite zu berücksichtigen ist: | ||
| + | :$$\frac{{\rm d\hspace{0.05cm}} p_{\rm B}(E)} {{\rm d}\hspace{0.05cm}E} = - \frac{\rm p_{\rm L}}{\sqrt{\rm 2\pi}\cdot {\sigma_d}} | ||
| + | \cdot {\rm exp}\left(- \frac{(s_0 + E)^2}{{\rm 2}\cdot | ||
| + | {\sigma_d}^2}\right)+\frac{\rm p_{\rm H}}{\sqrt{\rm 2\pi}\cdot | ||
| + | {\sigma_d}} \cdot {\rm exp}\left(- \frac{(s_0 - E)^2}{{\rm 2}\cdot | ||
| + | {\sigma_d}^2}\right) = 0$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \frac{p_{\rm L}} {p_{\rm H}} = - \frac{ | ||
| + | {\rm exp} \left(-\frac{(s_0 - E)^2}{{\rm 2}\cdot | ||
| + | {\sigma_d}^2}\right)}{{\rm exp} \left(-\frac{(s_0 + E)^2}{{\rm | ||
| + | 2}\cdot {\sigma_d}^2}\right)} = {\rm exp} \left( \frac{2 \cdot E | ||
| + | \cdot s_0 }{ {\sigma_d}^2}\right)\hspace{0.05cm}.$$ | ||
| + | *Damit erhält man für den optimalen Schwellenwert allgemein: | ||
| + | :$$E_{\rm opt} = \frac{\sigma_d^2} {2 \cdot s_0} \cdot {\rm ln}\hspace{0.05cm}\frac{p_{\rm L}} {p_{\rm H}} \hspace{0.05cm}.$$ | ||
| + | *Mit $σ_{d} = 0.5 \ \rm V$, $s_{\rm 0} = 1 \ \rm V$, $p_{\rm L} = 0.88$ und $p_{\rm H} = 0.12$ ergibt sich folgendes Optimum: | ||
| + | :$$E_{\rm opt} = \frac{(0.5\, {\rm V})^2} {2 \cdot 1\, {\rm V}} \cdot {\rm ln}\hspace{0.05cm}\frac{0.88} {0.12} \hspace{0.1cm}\underline { \approx 0.25\, {\rm V}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Die minimale Fehlerwahrscheinlichkeit für den optimalen Schwellenwert $E_{\rm opt} = 0.25 \hspace{0.05cm} \rm V$ ist somit: | ||
| + | :$$p_{\rm B, \hspace{0.05cm}min} = 0.88 \cdot {\rm Q}(2.5) + 0.12 \cdot {\rm Q}(1.5) = 0.88 \cdot 0.62\,\% + 0.12 \cdot 6.68\,\%\ \hspace{0.1cm}\underline {= 1.35\,\% }\hspace{0.05cm}.$$ | ||
| + | *Gegenüber $E = 0$ ist die Fehlerwahrscheinlichkeit nun um ca. $40 \%$ kleiner. | ||
| + | |||
| + | |||
| + | '''(6)''' Mit dem Ergebnis aus '''(4)''' ergibt sich nun für den optimalen Schwellenwert: | ||
| + | :$$E_{\rm opt} = \frac{(0.5\, {\rm V})^2} {2 \cdot 1\, {\rm V}} \cdot {\rm ln}\hspace{0.05cm}\frac{0.31} {0.69}\hspace{0.1cm}\underline { \approx -0.1\, {\rm V}}\hspace{0.05cm}.$$ | ||
| + | Bitte beachten Sie: | ||
| + | *Nachdem hier das Symbol '''$\rm L$''' unwahrscheinlicher ist, muss nun die Schwelle nach links – also weg vom wahrscheinlicheren Symbol – verschoben werden. | ||
| + | *Die Herleitung des Ergebnisses zu '''(4)''' und die Grafik auf der Angabenseite zeigen, dass der optimale Schwellenwert genau an die Stelle zu setzen ist, bei der sich die beiden Gaußfunktionen schneiden. | ||
| + | |||
| + | |||
| + | '''(7)''' Mit dem Ergebnis aus '''(6)''' gilt schließlich: | ||
| + | :$$p_{\rm B, \hspace{0.05cm}min} = 0.31 \cdot {\rm Q}(1.8) + 0.69 \cdot {\rm Q}(2.2) = 0.31 \cdot 3.59\,\% + 0.69 \cdot 1.39\,\%\ \hspace{0.1cm}\underline { = 2.07\,\% } \hspace{0.05cm}.$$ | ||
| + | *Aufgrund der weniger gravierenden Unsymmetrie ist die erreichbare Verbesserung mit $9 \%$ geringer als unter Punkt '''(5)''' berechnet. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 30. April 2022, 15:36 Uhr
In dieser Aufgabe wird ein bipolares Binärsystem mit AWGN–Rauschen ("Additive White Gaussian Noise") betrachtet, so dass für die Bitfehlerwahrscheinlichkeit gilt:
- $$p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)= {1}/{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2} \cdot \sigma_d}\right) \hspace{0.05cm}.$$
Hierbei sind folgende Funktionen verwendet:
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm},\hspace{1cm}{\rm erfc} ({\it x}) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
- Die obige Gleichung gilt für den Schwellenwert $E = 0$ unabhängig von den Symbolwahrscheinlichkeiten $p_{\rm L}$ und $p_{\rm H}$.
- Allerdings kann mit einem anderen Schwellenwert $E$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden, wenn die beiden Auftrittswahrscheinlichkeiten unterschiedlich sind $(p_{\rm L} ≠ p_{\rm H})$.
Die Streuung des Rauschanteils ist stets $σ_{d} = 0.5 \ \rm V$. Die beiden Amplituden des Detektionsnutzanteils sind mit $±1 \ \rm V$ fest vorgegeben.
Zu untersuchen sind folgende Symbolwahrscheinlichkeiten:
- $p_{\rm L} = 0.88$ ⇒ $p_{\rm H} = 1- p_{\rm L} =0.12$,
- $p_{\rm L} = 0.31$ ⇒ $p_{\rm H} = 1- p_{\rm L} =0.69$.
In der Grafik ist dieser letzte Parametersatz und der Schwellenwert $E =s_{\rm 0}/10$ berücksichtigt. Dargestellt ist die Wahrscheinlichkeitsdichtefunktion $\rm WDF$ der Detektionsabtastwerte $d$.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Fehlerwahrscheinlichkeit bei Basisbandübertragung".
- Zur Bestimmung von Fehlerwahrscheinlichkeiten können Sie das interaktive Applet "Komplementäre Gaußsche Fehlerfunktionen" verwenden.
- Für die Ableitung der Q–Funktion gilt:
- $$\frac{{\rm d\hspace{0.05cm}Q} ({\it x})} {{\rm d}\hspace{0.05cm}x} = \frac{\rm 1}{\sqrt{\rm 2\pi}} \cdot \rm e^{\it -x^{\rm 2}/\rm 2} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$\rm Q (\it x)= \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u = \frac{\rm 1}{\sqrt{\rm \pi}}\int_{\it x/\sqrt{\rm 2}}^{+\infty}\rm e^{\it -t^{\hspace{0.05cm}\rm 2}}\,{d \it t} = {1}/{2} \cdot {\rm erfc} \left( {x}/{\sqrt{2}} \right)\hspace{0.05cm}.$$
Daraus folgt die Richtigkeit des ersten Lösungsvorschlags:
- $${\rm erfc} (x)= 2 \cdot {\rm Q} (\sqrt{2} \cdot x) \hspace{0.05cm}.$$
(2) Unabhängig von den Symbolwahrscheinlichkeiten erhält man mit der Entscheiderschwelle $E = 0$:
- $$p_{\rm B} = {\rm Q} \left( {s_0}/{\sigma_d}\right)= {\rm Q} (2) \hspace{0.1cm}\underline {= 2.27 \, \% }\hspace{0.05cm}.$$
(3) Nun lautet die allgemeine Gleichung für die Bitfehlerwahrscheinlichkeit, wobei $d_{\rm N}$ den Rauschanteil von $d(t)$ bezeichnet:
- $$p_{\rm B} \ = \ p_{\rm L} \cdot {\rm Pr}( d_{\rm N}> E + s_0)+ p_{\rm H} \cdot {\rm Pr}( d_{\rm N}< E - s_0) \ = \ p_{\rm L} \cdot {\rm Q} \left( \frac{s_0 + E}{\sigma_d}\right)+ p_{\rm H} \cdot {\rm Q} \left( \frac{s_0 - E}{\sigma_d}\right)\hspace{0.05cm}.$$
- Hierbei ist die WDF-Symmetrie berücksichtigt. Mit $p_{\rm L} = 0.88$ ⇒ $p_{\rm H} = 0.12$ und $E = 0.1 \hspace{0.05cm} \rm V $ erhält man:
- $$p_{\rm B} \hspace{-0.05cm}=\hspace{-0.05cm} 0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{\rm Q} \left( \frac{1\, {\rm V} + 0.1\, {\rm V}}{0.5\, {\rm V}}\right)\hspace{-0.05cm}+\hspace{-0.05cm} 0.12 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{\rm Q} \left( \frac{1\, {\rm V} - 0.1\, {\rm V}}{0.5\, {\rm V}}\right) \hspace{-0.05cm}=\hspace{-0.05cm} 0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm} {\rm Q}(2.2) \hspace{-0.05cm}+\hspace{-0.05cm} 0.12 \cdot {\rm Q}(1.8) \hspace{-0.05cm}= \hspace{-0.05cm}0.88 \hspace{-0.03cm}\cdot \hspace{-0.03cm} 1.39\,\% \hspace{-0.05cm}+\hspace{-0.05cm} 0.12 \hspace{-0.03cm}\cdot \hspace{-0.03cm} 3.59\,\%\ \hspace{0.1cm}\underline { = 1.65\,\% } \hspace{0.05cm}.$$
- Durch die Schwellenverschiebung nach rechts um $E = s_{0}/10$ ergibt sich eine Verbesserung von $p_{\rm B} = 2.27 \ \%$ auf $p_{\rm B} = 1.65 \ \%$.
(4) Diese Optimierungsaufgabe wird durch Nullsetzen der Ableitung gelöst, wobei der Hinweis auf der Angabenseite zu berücksichtigen ist:
- $$\frac{{\rm d\hspace{0.05cm}} p_{\rm B}(E)} {{\rm d}\hspace{0.05cm}E} = - \frac{\rm p_{\rm L}}{\sqrt{\rm 2\pi}\cdot {\sigma_d}} \cdot {\rm exp}\left(- \frac{(s_0 + E)^2}{{\rm 2}\cdot {\sigma_d}^2}\right)+\frac{\rm p_{\rm H}}{\sqrt{\rm 2\pi}\cdot {\sigma_d}} \cdot {\rm exp}\left(- \frac{(s_0 - E)^2}{{\rm 2}\cdot {\sigma_d}^2}\right) = 0$$
- $$\Rightarrow \hspace{0.3cm} \frac{p_{\rm L}} {p_{\rm H}} = - \frac{ {\rm exp} \left(-\frac{(s_0 - E)^2}{{\rm 2}\cdot {\sigma_d}^2}\right)}{{\rm exp} \left(-\frac{(s_0 + E)^2}{{\rm 2}\cdot {\sigma_d}^2}\right)} = {\rm exp} \left( \frac{2 \cdot E \cdot s_0 }{ {\sigma_d}^2}\right)\hspace{0.05cm}.$$
- Damit erhält man für den optimalen Schwellenwert allgemein:
- $$E_{\rm opt} = \frac{\sigma_d^2} {2 \cdot s_0} \cdot {\rm ln}\hspace{0.05cm}\frac{p_{\rm L}} {p_{\rm H}} \hspace{0.05cm}.$$
- Mit $σ_{d} = 0.5 \ \rm V$, $s_{\rm 0} = 1 \ \rm V$, $p_{\rm L} = 0.88$ und $p_{\rm H} = 0.12$ ergibt sich folgendes Optimum:
- $$E_{\rm opt} = \frac{(0.5\, {\rm V})^2} {2 \cdot 1\, {\rm V}} \cdot {\rm ln}\hspace{0.05cm}\frac{0.88} {0.12} \hspace{0.1cm}\underline { \approx 0.25\, {\rm V}}\hspace{0.05cm}.$$
(5) Die minimale Fehlerwahrscheinlichkeit für den optimalen Schwellenwert $E_{\rm opt} = 0.25 \hspace{0.05cm} \rm V$ ist somit:
- $$p_{\rm B, \hspace{0.05cm}min} = 0.88 \cdot {\rm Q}(2.5) + 0.12 \cdot {\rm Q}(1.5) = 0.88 \cdot 0.62\,\% + 0.12 \cdot 6.68\,\%\ \hspace{0.1cm}\underline {= 1.35\,\% }\hspace{0.05cm}.$$
- Gegenüber $E = 0$ ist die Fehlerwahrscheinlichkeit nun um ca. $40 \%$ kleiner.
(6) Mit dem Ergebnis aus (4) ergibt sich nun für den optimalen Schwellenwert:
- $$E_{\rm opt} = \frac{(0.5\, {\rm V})^2} {2 \cdot 1\, {\rm V}} \cdot {\rm ln}\hspace{0.05cm}\frac{0.31} {0.69}\hspace{0.1cm}\underline { \approx -0.1\, {\rm V}}\hspace{0.05cm}.$$
Bitte beachten Sie:
- Nachdem hier das Symbol $\rm L$ unwahrscheinlicher ist, muss nun die Schwelle nach links – also weg vom wahrscheinlicheren Symbol – verschoben werden.
- Die Herleitung des Ergebnisses zu (4) und die Grafik auf der Angabenseite zeigen, dass der optimale Schwellenwert genau an die Stelle zu setzen ist, bei der sich die beiden Gaußfunktionen schneiden.
(7) Mit dem Ergebnis aus (6) gilt schließlich:
- $$p_{\rm B, \hspace{0.05cm}min} = 0.31 \cdot {\rm Q}(1.8) + 0.69 \cdot {\rm Q}(2.2) = 0.31 \cdot 3.59\,\% + 0.69 \cdot 1.39\,\%\ \hspace{0.1cm}\underline { = 2.07\,\% } \hspace{0.05cm}.$$
- Aufgrund der weniger gravierenden Unsymmetrie ist die erreichbare Verbesserung mit $9 \%$ geringer als unter Punkt (5) berechnet.