Aufgaben:Aufgabe 3.3: Rauschen bei Kanalentzerrung: Unterschied zwischen den Versionen
| (21 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1407__Dig_A_3_3.png |right|frame]] | + | [[Datei:P_ID1407__Dig_A_3_3.png |right|frame|Rausch–LDS vor dem Entscheider]] |
| − | Wir betrachten zwei unterschiedliche Systemvarianten, die beide NRZ–Rechteck–Sendeimpulse benutzen und durch AWGN–Rauschen beeinträchtigt werden. In beiden Fällen wird zur Rauschleistungsbegrenzung ein Gaußtiefpass | + | Wir betrachten zwei unterschiedliche Systemvarianten, die beide NRZ–Rechteck–Sendeimpulse benutzen und durch AWGN–Rauschen beeinträchtigt werden. |
| + | *In beiden Fällen wird zur Rauschleistungsbegrenzung ein Gaußtiefpass | ||
:$$H_{\rm G}(f) = {\rm exp}(- \pi \cdot | :$$H_{\rm G}(f) = {\rm exp}(- \pi \cdot | ||
\frac{f^2}{(2f_{\rm G})^2})$$ | \frac{f^2}{(2f_{\rm G})^2})$$ | ||
| − | mit der normierten Grenzfrequenz $ | + | :mit der normierten Grenzfrequenz $f_{\rm G} \cdot T = 0.35$ verwendet, so dass beide Systeme mit $\ddot{o}(T_{\rm D} = 0) = 0.478 \cdot s_0$ auch die gleiche Augenöffnung aufweisen. |
| − | Die beiden Systeme unterscheiden sich wie folgt | + | |
| − | * Der Kanalfrequenzgang von System A ist frequenzunabhängig: $H_{\rm K}(f) = \alpha$. Für das Empfangsfilter ist demnach $H_{\rm E}(f) = H_{\rm G}(f)/\alpha$ anzusetzen, so dass für die Detektionsrauschleistung gilt: | + | *Die pro Bit aufgewendete Sendeenergie $E_{\rm B} = s_0^2 \cdot T$ ist um den Faktor $10^9$ größer als die Rauschleistungsdichte $N_0$ ⇒ $10\cdot {\rm lg} \, E_{\rm B}/N_0 = 90 \, {\rm dB}$. |
| + | |||
| + | |||
| + | Die beiden Systeme unterscheiden sich wie folgt: | ||
| + | * Der Kanalfrequenzgang von System $\rm A$ ist frequenzunabhängig: $H_{\rm K}(f) = \alpha$. Für das Empfangsfilter ist demnach $H_{\rm E}(f) = H_{\rm G}(f)/\alpha$ anzusetzen, so dass für die Detektionsrauschleistung gilt: | ||
:$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} | :$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} | ||
|H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} | |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} | ||
\cdot \alpha^2} \hspace{0.05cm}.$$ | \cdot \alpha^2} \hspace{0.05cm}.$$ | ||
| − | * Dagegen ist für System B ein Koaxialkabel mit der charakteristischen Dämpfung (bei der halben Bitrate) $a_* = 80 \, {\rm dB}$ (bzw. $9.2 \, {\rm Np}$ | + | * Dagegen ist für System $\rm B$ ein Koaxialkabel mit der charakteristischen Dämpfung (bei der halben Bitrate) $a_* = 80 \, {\rm dB}$ $($bzw. $9.2 \, {\rm Np})$ vorausgesetzt, so dass für den Betragsfrequenzgang gilt: |
| − | :$$|H_{\rm K}(f)| = {\rm | + | :$$|H_{\rm K}(f)| = {\rm e}^{- 9.2 \hspace{0.05cm} \cdot |
| − | \hspace{0.05cm}\sqrt{2 f T} | + | \hspace{0.05cm}\sqrt{2 f T}}\hspace{0.05cm}.$$ |
| − | * Somit lautet die Gleichung für die Rauschleistungsdichte vor dem Entscheider (mit $ | + | * Somit lautet die Gleichung für die Rauschleistungsdichte vor dem Entscheider $($mit $f_{\rm G} \cdot T = 0.35)$: |
:$${\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot \frac{|H_{\rm G | :$${\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot \frac{|H_{\rm G | ||
}(f)|^2}{|H_{\rm K}(f)|^2} = {N_0}/{2} \cdot {\rm exp}\left | }(f)|^2}{|H_{\rm K}(f)|^2} = {N_0}/{2} \cdot {\rm exp}\left | ||
| Zeile 23: | Zeile 28: | ||
\right ] \hspace{0.05cm}.$$ | \right ] \hspace{0.05cm}.$$ | ||
| − | Dieser Funktionsverlauf ist in obiger Grafik rot dargestellt. Die Rauchleistungsdichte für das System A ist blau gezeichnet. | + | Dieser Funktionsverlauf $\rm B$ ist in obiger Grafik rot dargestellt. Die Rauchleistungsdichte für das System $\rm A$ ist blau gezeichnet. |
| − | Für das System B wurde messtechnisch die ungünstigste Fehlerwahrscheinlichkeit | + | Für das System $\rm B$ wurde messtechnisch die ungünstigste Fehlerwahrscheinlichkeit |
:$$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} | :$$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} | ||
\right) \hspace{0.2cm}{\rm mit} \hspace{0.2cm} \rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}$$ | \right) \hspace{0.2cm}{\rm mit} \hspace{0.2cm} \rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}$$ | ||
| − | bestimmt. Die Messung ergab $ | + | bestimmt. Die Messung ergab $p_{\rm U} = 4 \cdot 10^{\rm -8}$, was dem Störabstand $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$ entspricht. |
| + | |||
| + | |||
| − | '' | + | |
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Ber%C3%BCcksichtigung_von_Kanalverzerrungen_und_Entzerrung|"Berücksichtigung von Kanalverzerrungen und Entzerrung"]]. | ||
| + | |||
| + | * Verwenden Sie zur numerischen Auswertung der Q–Funktion das Interaktionsmodul [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Komplementäre Gaußsche Fehlerfunktionen"]]. | ||
| + | |||
| + | |||
| Zeile 38: | Zeile 52: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welcher Störeffektivwert tritt bei System B auf? | + | {Welcher (normierter) Störeffektivwert tritt bei System $\rm B$ auf? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_d/s_0 \ = \ $ { 0.044 3% } |
| − | {Welcher Störeffektivwert tritt bei System A auf, wenn dieses zur genau gleichen (ungünstigsten) Fehlerwahrscheinlichkeit wie das System | + | {Welcher Störeffektivwert tritt bei System $\rm A$ auf, wenn dieses zur genau gleichen (ungünstigsten) Fehlerwahrscheinlichkeit wie das System $\rm B$ führt? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_d/s_0 \ = \ $ { 0.044 3% } |
| − | {Mit welchem Dämpfungsfaktor \alpha ist das System A dem System B bezüglich der (ungünstigsten) Fehlerwahrscheinlichkeit äquivalent? | + | {Mit welchem Dämpfungsfaktor $\alpha$ ist das System $\rm A$ dem System $\rm B$ bezüglich der (ungünstigsten) Fehlerwahrscheinlichkeit äquivalent? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm | + | $20 \cdot {\rm lg} \ \alpha \ = \ $ { -70.967--66.833 } ${\ \rm dB}$ |
| − | {Wie groß ist die auf $N_0/2$ bezogene Rauschleistungsdichte (bei $f = 0$ | + | {Wie groß ist die auf $N_0/2$ bezogene Rauschleistungsdichte $($bei $f = 0)$ vor dem Entscheider für System $\rm A$ bzw. System $\rm B$? |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System A:}\hspace{0.4cm} {\it \Phi}_{d \rm N} (f = 0)/(N_0/2) \ = \ $ { 7.8 3% } $\ \cdot 10^6$ |
| − | ${ | + | $\text{System B:}\hspace{0.42cm} {\it \Phi}_{d \rm N} (f = 0)/(N_0/2) \ = \ $ { 1 3% } $\ \cdot 10^0$ |
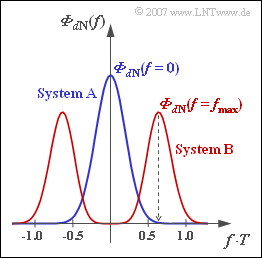
| − | {Für den Rest der Aufgabe betrachten wir ausschließlich das System B. Bei welcher Frequenz $f_{\rm max}$ besitzt $\ | + | {Für den Rest der Aufgabe betrachten wir ausschließlich das System $\rm B$. Bei welcher Frequenz $f_{\rm max}$ besitzt ${\it \Phi}_{d \rm N}(f)$ sein Maximum? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm max} \cdot T\ = \ ${ 0.63 3% } |
| − | {Um welchen Faktor ist die Rauschleistungsdichte bei der Frequenz $f_{\rm max}$ größer als bei $f = 0$? | + | {Um welchen Faktor ist die Rauschleistungsdichte bei der Frequenz $f_{\rm max}$ größer als bei $f = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\it \Phi}_{d \rm N}(f_{\rm max})/{\it \Phi}_{d \rm N}(0)\ = \ $ { 5.4 3% } $\ \cdot 10^6$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Aus $10 \cdot {\rm lg} \, \ | + | '''(1)''' Aus $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$ folgt $\rho_{\rm U} = 10^{\rm 1.48} ≈ 30.2$ und weiter mit der angegebenen Gleichung: |
:$$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow | :$$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} | \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} | ||
| Zeile 72: | Zeile 86: | ||
| − | '''(2)''' Bei gleicher Fehlerwahrscheinlichkeit $\ | + | '''(2)''' Bei gleicher Fehlerwahrscheinlichkeit $p_{\rm U}$ $($und damit gleichem $\rho_{\rm U})$ muss $\sigma_d$ genau den gleichen Wert besitzen wie in der Teilaufgabe '''(1)''' berechnet, da auch die Augenöffnung gleich bleibt ⇒ $\sigma_d/s_0 \underline{= 0.044}.$ |
| − | '''(3)''' Entsprechend dem Angabenblatt gilt: | + | '''(3)''' Entsprechend dem Angabenblatt gilt: |
:$$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} | :$$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} | ||
= \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} | = \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} | ||
\cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot | \cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot | ||
| − | T}{\sqrt{2} \cdot (\sigma_d/s_0)^2} | + | T}{\sqrt{2} \cdot (\sigma_d/s_0)^2}\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} \alpha^2 = 10^{-9} \cdot \frac{ | |
0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} | 0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In ${\rm dB}$ ausgedrückt erhält man somit | + | In ${\rm dB}$ ausgedrückt erhält man somit |
:$$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = | :$$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = | ||
-70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = | -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = | ||
| Zeile 90: | Zeile 104: | ||
| − | '''(4)''' Beim System B ist wegen $ | + | '''(4)''' Beim System $\rm B$ ist wegen $H_{\rm E}(f = 0) = 1$ der normierte Wert gleich $1$, das heißt, es ist ${\it \Phi}_{d \rm N}(f = 0) = N_0/2$. |
| − | |||
| − | |||
| + | *Dagegen ist bei System $\rm A$ dieser Wert aufgrund der Komponenten der frequenzunabhängigen Kabeldämpfung $\alpha$ um $1/\alpha^2$ größer: | ||
| + | :$${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, \hspace{1.05cm}{\rm System\hspace{0.15cm}B}: \frac{{\it \Phi}_{d \rm N}(f = 0)}{N_0/2} \, \underline {= 1}.$$ | ||
| − | '''(5)''' $\ | + | |
| + | '''(5)''' ${\it \Phi}_{d \rm N}(f)$ ist maximal, wenn der Exponent | ||
:$$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$ | :$$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$ | ||
| − | den maximalen Wert besitzt. Mit $x = f \cdot T$ gilt somit für die Optimierungsfunktion: | + | den maximalen Wert besitzt. Mit $x = f \cdot T$ gilt somit für die Optimierungsfunktion: |
:$$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot | :$$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot | ||
| − | \sqrt{x} - 13 \cdot x^2 | + | \sqrt{x} - 13 \cdot x^2 \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} \frac{{\rm d}y}{{\rm d}x} = \frac{26} | |
{2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$ | {2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$ | ||
:$$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x | :$$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot | ||
x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 | x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 | ||
| − | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x \approx 0.63 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Damit ergibt sich $f_{\rm max} \cdot T | + | Damit ergibt sich $f_{\rm max} \cdot T\hspace{0.15cm}\underline {\approx 0.63}$. |
| − | '''(6)''' Mit $x_{\rm max} = 0.63$ erhält man den Funktionswert | + | '''(6)''' Mit $x_{\rm max} = 0.63$ erhält man den Funktionswert |
| + | |||
| + | [[Datei:P_ID1408__Dig_A_3_3f.png|frame|right|Rauschanteil $d_{\rm N}(t)$]] | ||
:$$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 | :$$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 | ||
\hspace{0.15cm}\underline {\approx 15.477}.$$ | \hspace{0.15cm}\underline {\approx 15.477}.$$ | ||
| + | Daraus folgt: | ||
| + | *Die Rauschleistungsdichte ist bei der (normierten) Frequenz $f \cdot T \approx 0.63$ um den Faktor $e^{\rm 15.5} \underline{\approx 5.4 \cdot 10^6}$ größer ist als bei der Frequenz $f = 0$. | ||
| + | |||
| + | *Im Rauschanteil $d_{\rm N}(t)$ überwiegen somit periodische Anteile mit der Periodendauer $T_0 \approx 1.6 \cdot T$. | ||
| + | |||
| + | *Die Grafik zeigt eine Simulation und bestätigt dieses Ergebnis. | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 19. Juni 2022, 11:36 Uhr
Wir betrachten zwei unterschiedliche Systemvarianten, die beide NRZ–Rechteck–Sendeimpulse benutzen und durch AWGN–Rauschen beeinträchtigt werden.
- In beiden Fällen wird zur Rauschleistungsbegrenzung ein Gaußtiefpass
- $$H_{\rm G}(f) = {\rm exp}(- \pi \cdot \frac{f^2}{(2f_{\rm G})^2})$$
- mit der normierten Grenzfrequenz $f_{\rm G} \cdot T = 0.35$ verwendet, so dass beide Systeme mit $\ddot{o}(T_{\rm D} = 0) = 0.478 \cdot s_0$ auch die gleiche Augenöffnung aufweisen.
- Die pro Bit aufgewendete Sendeenergie $E_{\rm B} = s_0^2 \cdot T$ ist um den Faktor $10^9$ größer als die Rauschleistungsdichte $N_0$ ⇒ $10\cdot {\rm lg} \, E_{\rm B}/N_0 = 90 \, {\rm dB}$.
Die beiden Systeme unterscheiden sich wie folgt:
- Der Kanalfrequenzgang von System $\rm A$ ist frequenzunabhängig: $H_{\rm K}(f) = \alpha$. Für das Empfangsfilter ist demnach $H_{\rm E}(f) = H_{\rm G}(f)/\alpha$ anzusetzen, so dass für die Detektionsrauschleistung gilt:
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \alpha^2} \hspace{0.05cm}.$$
- Dagegen ist für System $\rm B$ ein Koaxialkabel mit der charakteristischen Dämpfung (bei der halben Bitrate) $a_* = 80 \, {\rm dB}$ $($bzw. $9.2 \, {\rm Np})$ vorausgesetzt, so dass für den Betragsfrequenzgang gilt:
- $$|H_{\rm K}(f)| = {\rm e}^{- 9.2 \hspace{0.05cm} \cdot \hspace{0.05cm}\sqrt{2 f T}}\hspace{0.05cm}.$$
- Somit lautet die Gleichung für die Rauschleistungsdichte vor dem Entscheider $($mit $f_{\rm G} \cdot T = 0.35)$:
- $${\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot \frac{|H_{\rm G }(f)|^2}{|H_{\rm K}(f)|^2} = {N_0}/{2} \cdot {\rm exp}\left [18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{(2 \cdot 0.35)^2} \right ] \hspace{0.05cm}.$$
Dieser Funktionsverlauf $\rm B$ ist in obiger Grafik rot dargestellt. Die Rauchleistungsdichte für das System $\rm A$ ist blau gezeichnet.
Für das System $\rm B$ wurde messtechnisch die ungünstigste Fehlerwahrscheinlichkeit
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) \hspace{0.2cm}{\rm mit} \hspace{0.2cm} \rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}$$
bestimmt. Die Messung ergab $p_{\rm U} = 4 \cdot 10^{\rm -8}$, was dem Störabstand $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$ entspricht.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Berücksichtigung von Kanalverzerrungen und Entzerrung".
- Verwenden Sie zur numerischen Auswertung der Q–Funktion das Interaktionsmodul "Komplementäre Gaußsche Fehlerfunktionen".
Fragebogen
Musterlösung
- $$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} \hspace{0.15cm}\underline { \approx 0.044 \cdot s_0 }\hspace{0.05cm}.$$
(2) Bei gleicher Fehlerwahrscheinlichkeit $p_{\rm U}$ $($und damit gleichem $\rho_{\rm U})$ muss $\sigma_d$ genau den gleichen Wert besitzen wie in der Teilaufgabe (1) berechnet, da auch die Augenöffnung gleich bleibt ⇒ $\sigma_d/s_0 \underline{= 0.044}.$
(3) Entsprechend dem Angabenblatt gilt:
- $$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot T}{\sqrt{2} \cdot (\sigma_d/s_0)^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha^2 = 10^{-9} \cdot \frac{ 0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} \hspace{0.05cm}.$$
In ${\rm dB}$ ausgedrückt erhält man somit
- $$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = -68.9\,{\rm dB}} \hspace{0.05cm}.$$
(4) Beim System $\rm B$ ist wegen $H_{\rm E}(f = 0) = 1$ der normierte Wert gleich $1$, das heißt, es ist ${\it \Phi}_{d \rm N}(f = 0) = N_0/2$.
- Dagegen ist bei System $\rm A$ dieser Wert aufgrund der Komponenten der frequenzunabhängigen Kabeldämpfung $\alpha$ um $1/\alpha^2$ größer:
- $${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, \hspace{1.05cm}{\rm System\hspace{0.15cm}B}: \frac{{\it \Phi}_{d \rm N}(f = 0)}{N_0/2} \, \underline {= 1}.$$
(5) ${\it \Phi}_{d \rm N}(f)$ ist maximal, wenn der Exponent
- $$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$
den maximalen Wert besitzt. Mit $x = f \cdot T$ gilt somit für die Optimierungsfunktion:
- $$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot \sqrt{x} - 13 \cdot x^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{{\rm d}y}{{\rm d}x} = \frac{26} {2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$
- $$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x \approx 0.63 \hspace{0.05cm}.$$
Damit ergibt sich $f_{\rm max} \cdot T\hspace{0.15cm}\underline {\approx 0.63}$.
(6) Mit $x_{\rm max} = 0.63$ erhält man den Funktionswert
- $$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 \hspace{0.15cm}\underline {\approx 15.477}.$$
Daraus folgt:
- Die Rauschleistungsdichte ist bei der (normierten) Frequenz $f \cdot T \approx 0.63$ um den Faktor $e^{\rm 15.5} \underline{\approx 5.4 \cdot 10^6}$ größer ist als bei der Frequenz $f = 0$.
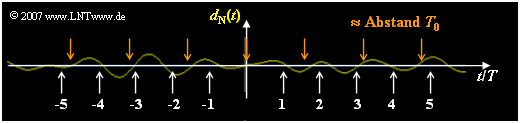
- Im Rauschanteil $d_{\rm N}(t)$ überwiegen somit periodische Anteile mit der Periodendauer $T_0 \approx 1.6 \cdot T$.
- Die Grafik zeigt eine Simulation und bestätigt dieses Ergebnis.