Aufgaben:Aufgabe 3.5: Augenöffnung bei Pseudoternärcodierung: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
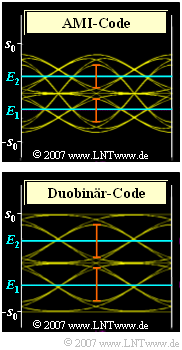
| − | [[Datei:P_ID1421__Dig_A_3_5.png|right|frame| | + | [[Datei:P_ID1421__Dig_A_3_5.png|right|frame|Augendiagramme beim AMI– und Duobinärcode]] |
| − | Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften: | + | Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften: |
| − | * NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$, | + | * NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$, |
| − | * Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$, | + | |
| − | * AWGN–Rauschen mit der Rauschleistungsdichte $N_0$, | + | * Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$, |
| − | * Empfangsfilter, bestehend aus einem idealen Kanalentzerrer und einem Gaußtiefpass mit der normierten Grenzfrequenz $f_{\rm G} \cdot T \approx 0.5$. | + | |
| − | * Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_{\rm D} = 0$. | + | * AWGN–Rauschen mit der Rauschleistungsdichte $N_0$, |
| + | |||
| + | * Empfangsfilter $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f) $, bestehend aus einem idealen Kanalentzerrer $H_{\rm K}(f)^{-1}$ und einem Gaußtiefpass $H_{\rm G}(f)$ mit der normierten Grenzfrequenz $f_{\rm G} \cdot T \approx 0.5$. | ||
| + | |||
| + | * Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_{\rm D} = 0$. | ||
Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes: | Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes: | ||
| − | + | ⇒ Das $\text{System A}$ verwendet ein binäres bipolares redundanzfreies Sendesignal. Bekannt sind folgende Beschreibungsgrößen: | |
| − | * Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, ... \, \approx 0$ | + | * Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$ |
:$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} | :$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} | ||
-g_{1}-g_{-1} = 1.12\,{\rm V} | -g_{1}-g_{-1} = 1.12\,{\rm V} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * Rauscheffektivwert $\sigma_d \approx | + | * Rauscheffektivwert $\sigma_d \approx 0.2 \, {\rm V}$ |
| − | :$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ | + | :$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ |
\sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$ | 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | + | ⇒ Das $\text{System B}$ verwendet AMI–Codierung: | |
| + | *Hier treten die äußeren Symbole $„+1”$ bzw. $„–1”$ nur isoliert auf. | ||
| + | |||
| + | *Bei drei aufeinanderfolgenden Symbolen sind unter anderem die Folgen „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$” und „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...} $” nicht möglich, | ||
| + | : im Gegensatz zur Folge „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...} $”. | ||
| + | |||
| + | |||
| + | ⇒ Das $\text{System C}$ verwendet den Duobinärcode: | ||
| + | *Hier wird die alternierende Folge „$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...} $” durch den Code ausgeschlossen, was sich günstig auf die Augenöffnung auswirkt. | ||
| + | |||
| − | |||
| − | + | ||
| − | * | + | Hinweise: |
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Impulsinterferenzen_bei_mehrstufiger_%C3%9Cbertragung|"Impulsinterferenzen bei mehrstufiger Übertragung"]]. | ||
| + | |||
* Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich. | * Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die halbe Augenöffnung für den AMI–Code. | + | {Berechnen Sie die halbe Augenöffnung für den '''AMI–Code'''. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System B:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ { 0.45 3% } $\ {\rm V}$ |
{Berechnen Sie den ungünstigsten Störabstand dieses Systems. | {Berechnen Sie den ungünstigsten Störabstand dieses Systems. | ||
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System B:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ { 7 3% } $\ {\rm dB}$ |
| − | {Wie müssen die Schwellenwerte $E_1$ und $E_2$ gewählt werden, damit das soeben berechnete Ergebnis stimmt? | + | {Wie müssen die Schwellenwerte $E_1$ und $E_2$ gewählt werden, damit das soeben berechnete Ergebnis stimmt? |
|type="{}"} | |type="{}"} | ||
| − | $E_1$ | + | $E_1 \ \hspace{0.05cm} = \ ${ -0.69--0.65 } $\ {\rm V}$ |
| − | $E_2$ | + | $E_2 \ = \ $ { 0.667 3% } $\ {\rm V}$ |
| − | {Berechnen Sie die halbe Augenöffnung beim Duobinär–Code. | + | {Berechnen Sie die halbe Augenöffnung beim '''Duobinär–Code'''. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System C:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ { 0.67 3% } $\ {\rm V}$ |
| − | {Berechnen Sie den ungünstigsten Störabstand bei Duobinärcodierung. | + | {Berechnen Sie den ungünstigsten Störabstand bei der Duobinärcodierung. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System C:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ { 10.5 3% } $\ {\rm dB}$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Da beim AMI–Code die Symbolrate gegenüber dem redundanzfreien Binärsystem nicht verändert wird, bleiben die Grundimpulswerte $g_0 = 1.56 \, {\rm V}, g_1 = g_{\rm –1} = 0.22 \, {\rm V} | + | '''(1)''' Da beim AMI–Code die Symbolrate gegenüber dem redundanzfreien Binärsystem nicht verändert wird, bleiben die Grundimpulswerte unverändert: |
| + | :$$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$ | ||
| + | |||
| + | Bei Pseudoternärcodierung gibt es stets zwei Augenöffnungen: | ||
| − | + | *Die obere Begrenzungslinie des oberen Auges ergibt sich beim AMI–Code wie beim redundanzfreien Binärsystem: | |
:$$d_{\rm oben}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm | :$$d_{\rm oben}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm | ||
Folge:}-1, +1, -1{\rm )} | Folge:}-1, +1, -1{\rm )} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Dagegen gilt für die untere Begrenzungslinie des oberen Auges: | + | *Dagegen gilt für die untere Begrenzungslinie des oberen Auges: |
:$$d_{\rm unten}= g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm | :$$d_{\rm unten}= g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm | ||
| − | + | Folgen:}\hspace{0.2cm}0, \hspace{0.05cm}0, +1\hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}+1, \hspace{0.05cm}0, \hspace{0.05cm}0{\rm )}\hspace{0.05cm}.$$ | |
Für die halbe Augenöffnung gilt somit: | Für die halbe Augenöffnung gilt somit: | ||
| Zeile 74: | Zeile 92: | ||
0.45\,{\rm V}}\hspace{0.05cm}.$$ | 0.45\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | Die entsprechende Gleichung für das redundanzfreie Binärsystem lautet: | + | Die entsprechende Gleichung für das redundanzfreie Binärsystem lautet: |
:$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$ | :$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$ | ||
| − | '''(2)''' Bezüglich des Rauschens gibt es keinen Unterschied zwischen den Systemen | + | |
| + | '''(2)''' Bezüglich des Rauschens gibt es keinen Unterschied zwischen den drei Systemen, da stets die gleiche Symbolrate vorliegt. Daraus folgt für den AMI–Code: | ||
:$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = | :$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = | ||
5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Zeile 84: | Zeile 103: | ||
lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$ | lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | Die Einbuße gegenüber dem redundanzfreien Binärsystem beträgt somit fast $8 \, {\rm dB}$. Der Grund für diesen gravierenden Störabstandverlust ist, dass beim AMI& | + | *Die Einbuße gegenüber dem redundanzfreien Binärsystem beträgt somit fast $8 \, {\rm dB}$. |
| + | |||
| + | *Der Grund für diesen gravierenden Störabstandverlust ist, dass beim AMI–Code trotz $37\%$ Redundanz die bezüglich der Impulsinterferenzen besonders ungünstige Symbolfolge $\text{ ...} , \, –1, \, +1, \, –1, \text{ ...} $ nicht ausgeschlossen wird. | ||
| + | |||
| − | '''(3)''' Die Schwelle $E_2$ muss in der Mitte zwischen $d_{\rm oben}$ und $d_{\rm unten}$ liegen: | + | '''(3)''' Die Schwelle $E_2$ muss in der Mitte zwischen $d_{\rm oben}$ und $d_{\rm unten}$ liegen: |
:$$E_2= {1}/{2} \cdot (d_{\rm oben} + d_{\rm unten}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= | :$$E_2= {1}/{2} \cdot (d_{\rm oben} + d_{\rm unten}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= | ||
0.67\,{\rm V}}\hspace{0.05cm}.$$ | 0.67\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | *Der Schwellenwert $E_1$ liegt symmetrisch dazu: $E_1 \, \underline {= \, –0.67 {\rm V}}$. | ||
| − | |||
| − | '''(4)''' Wir gehen wieder von den gleichen Grundimpulswerten aus. Die ungünstigste Folge bezüglich der oberen Begrenzungslinie des oberen Auges ist $ | + | '''(4)''' Wir gehen wieder von den gleichen Grundimpulswerten aus. |
| + | *Die ungünstigste Folge bezüglich der oberen Begrenzungslinie des oberen Auges ist "$\text{ ...} , 0, \, +1, \, 0, \text{ ...} $", | ||
| + | *während die untere Begrenzungslinie durch "$\text{ ...} , 0, \, 0, \, +1, \text{ ...} $" bzw. "$\text{ ...} , +1, \, 0, \, 0, \text{ ...} $" bestimmt wird. | ||
| + | |||
| + | *Daraus folgt: | ||
:$$d_{\rm oben}= g_0, \hspace{0.2cm} d_{\rm unten} = g_1 \hspace{0.3cm}\Rightarrow | :$$d_{\rm oben}= g_0, \hspace{0.2cm} d_{\rm unten} = g_1 \hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - | \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - | ||
| − | {g_1}/{2}\hspace{0.15cm}\underline { = 0. | + | {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$ |
| − | '''(5)''' Mit dem Ergebnis aus 4) erhält man analog zur Teilaufgabe 2) | + | '''(5)''' Mit dem Ergebnis aus '''(4)''' erhält man analog zur Teilaufgabe '''(2)''': |
:$$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = | :$$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = | ||
11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Zeile 107: | Zeile 133: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Voraussetzung für dieses Ergebnis sind Schwellenwerte bei | + | *Voraussetzung für dieses Ergebnis sind Schwellenwerte bei |
:$$E_2= {1}/{2} \cdot (g_0 + g_1 ) = | :$$E_2= {1}/{2} \cdot (g_0 + g_1 ) = | ||
0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$ | 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$ | ||
| − | Anzumerken ist, dass hier stets von der gleichen Grenzfrequenz $ | + | *Anzumerken ist, dass hier stets von der gleichen Grenzfrequenz $f_{\rm G} \cdot T = 0.5$ ausgegangen wurde. |
| − | Bei Optimierung der Grenzfrequenz kann es durchaus sein, dass der Duobinärcode dem redundanzfreien Binärcode überlegen | + | |
| + | *Bei Optimierung der Grenzfrequenz kann es durchaus sein, dass der Duobinärcode bei hinreichend großer charakteristischer Kabeldämpfung dem redundanzfreien Binärcode überlegen ist. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Digitalsignalübertragung|^3.4 | + | [[Category:Aufgaben zu Digitalsignalübertragung|^3.4 Auge bei mehrstufigen Systemen^]] |
Aktuelle Version vom 21. Juni 2022, 15:38 Uhr
Betrachtet werden drei Nachrichtenübertragungssysteme, jeweils mit folgenden übereinstimmenden Eigenschaften:
- NRZ–Rechteckimpulse mit der Amplitude $s_0 = 2 \, {\rm V}$,
- Koaxialkabel mit charakteristischer Kabeldämpfung $a_* = 40 \, {\rm dB}$,
- AWGN–Rauschen mit der Rauschleistungsdichte $N_0$,
- Empfangsfilter $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f) $, bestehend aus einem idealen Kanalentzerrer $H_{\rm K}(f)^{-1}$ und einem Gaußtiefpass $H_{\rm G}(f)$ mit der normierten Grenzfrequenz $f_{\rm G} \cdot T \approx 0.5$.
- Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt $T_{\rm D} = 0$.
Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes:
⇒ Das $\text{System A}$ verwendet ein binäres bipolares redundanzfreies Sendesignal. Bekannt sind folgende Beschreibungsgrößen:
- Grundimpulswerte $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$
- $$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$
- Rauscheffektivwert $\sigma_d \approx 0.2 \, {\rm V}$
- $$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$
⇒ Das $\text{System B}$ verwendet AMI–Codierung:
- Hier treten die äußeren Symbole $„+1”$ bzw. $„–1”$ nur isoliert auf.
- Bei drei aufeinanderfolgenden Symbolen sind unter anderem die Folgen „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$” und „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...} $” nicht möglich,
- im Gegensatz zur Folge „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...} $”.
⇒ Das $\text{System C}$ verwendet den Duobinärcode:
- Hier wird die alternierende Folge „$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...} $” durch den Code ausgeschlossen, was sich günstig auf die Augenöffnung auswirkt.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Impulsinterferenzen bei mehrstufiger Übertragung".
- Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich.
Fragebogen
Musterlösung
- $$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$
Bei Pseudoternärcodierung gibt es stets zwei Augenöffnungen:
- Die obere Begrenzungslinie des oberen Auges ergibt sich beim AMI–Code wie beim redundanzfreien Binärsystem:
- $$d_{\rm oben}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folge:}-1, +1, -1{\rm )} \hspace{0.05cm}.$$
- Dagegen gilt für die untere Begrenzungslinie des oberen Auges:
- $$d_{\rm unten}= g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folgen:}\hspace{0.2cm}0, \hspace{0.05cm}0, +1\hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}+1, \hspace{0.05cm}0, \hspace{0.05cm}0{\rm )}\hspace{0.05cm}.$$
Für die halbe Augenöffnung gilt somit:
- $${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm oben} - d_{\rm unten}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= 0.45\,{\rm V}}\hspace{0.05cm}.$$
Die entsprechende Gleichung für das redundanzfreie Binärsystem lautet:
- $${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$
(2) Bezüglich des Rauschens gibt es keinen Unterschied zwischen den drei Systemen, da stets die gleiche Symbolrate vorliegt. Daraus folgt für den AMI–Code:
- $$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$
- Die Einbuße gegenüber dem redundanzfreien Binärsystem beträgt somit fast $8 \, {\rm dB}$.
- Der Grund für diesen gravierenden Störabstandverlust ist, dass beim AMI–Code trotz $37\%$ Redundanz die bezüglich der Impulsinterferenzen besonders ungünstige Symbolfolge $\text{ ...} , \, –1, \, +1, \, –1, \text{ ...} $ nicht ausgeschlossen wird.
(3) Die Schwelle $E_2$ muss in der Mitte zwischen $d_{\rm oben}$ und $d_{\rm unten}$ liegen:
- $$E_2= {1}/{2} \cdot (d_{\rm oben} + d_{\rm unten}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= 0.67\,{\rm V}}\hspace{0.05cm}.$$
- Der Schwellenwert $E_1$ liegt symmetrisch dazu: $E_1 \, \underline {= \, –0.67 {\rm V}}$.
(4) Wir gehen wieder von den gleichen Grundimpulswerten aus.
- Die ungünstigste Folge bezüglich der oberen Begrenzungslinie des oberen Auges ist "$\text{ ...} , 0, \, +1, \, 0, \text{ ...} $",
- während die untere Begrenzungslinie durch "$\text{ ...} , 0, \, 0, \, +1, \text{ ...} $" bzw. "$\text{ ...} , +1, \, 0, \, 0, \text{ ...} $" bestimmt wird.
- Daraus folgt:
- $$d_{\rm oben}= g_0, \hspace{0.2cm} d_{\rm unten} = g_1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$
(5) Mit dem Ergebnis aus (4) erhält man analog zur Teilaufgabe (2):
- $$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 10.5\,{\rm dB}} \hspace{0.05cm}.$$
- Voraussetzung für dieses Ergebnis sind Schwellenwerte bei
- $$E_2= {1}/{2} \cdot (g_0 + g_1 ) = 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$
- Anzumerken ist, dass hier stets von der gleichen Grenzfrequenz $f_{\rm G} \cdot T = 0.5$ ausgegangen wurde.
- Bei Optimierung der Grenzfrequenz kann es durchaus sein, dass der Duobinärcode bei hinreichend großer charakteristischer Kabeldämpfung dem redundanzfreien Binärcode überlegen ist.