Aufgaben:Aufgabe 3.3Z: Optimierung eines Koaxialkabelsystems: Unterschied zwischen den Versionen
Aus LNTwww
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1409__Dig_Z_3_3.png|right|frame| | + | [[Datei:P_ID1409__Dig_Z_3_3.png|right|frame|Normierte Systemgrößen für verschiedene Grenzfrequenzen]] |
Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen: | Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen: | ||
| − | * Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_{\rm B} = s_0^2 \cdot T$ | + | * Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_{\rm B} = s_0^2 \cdot T$. |
| − | |||
| − | |||
| − | |||
| + | * Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$. | ||
| − | Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_{\rm D})$ sowie den Detektionsrauscheffektivwert $\sigma_{\rm d}$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_{\rm G}$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit möglichst klein ist, wobei folgende Definition gilt: | + | * Es liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_{\rm B}$ vor. |
| + | |||
| + | * Der Empfängerfrequenzgang $H_{\rm E}(f)$ beinhaltet einen idealen Kanalentzerrer $H_{\rm K}^{\rm -1}(f)$ und einen Gaußtiefpass $H_{\rm G}(f)$ mit Grenzfrequenz $f_{\rm G}$ zur Rauschleistungsbegrenzung. | ||
| + | |||
| + | |||
| + | Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_{\rm D})$ sowie den Detektionsrauscheffektivwert $\sigma_{\rm d}$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_{\rm G}$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit möglichst klein ist, wobei folgende Definition gilt: | ||
:$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} | :$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} | ||
\right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$ | \right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$ | ||
| − | * | + | *Diese Größe ist eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S} \le p_{\rm U}$. |
| − | *Für $f_{\rm G} \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden: $ | + | |
| − | + | *Für $f_{\rm G} \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden: $p_{\rm S} \ge p_{\rm U}/4$. | |
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Ber%C3%BCcksichtigung_von_Kanalverzerrungen_und_Entzerrung|"Berücksichtigung von Kanalverzerrungen und Entzerrung"]]. | ||
| − | + | * Verwenden Sie zur numerischen Auswertung der Q–Funktion das Interaktionsmodul [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Komplementäre Gaußsche Fehlerfunktionen]]. | |
| − | + | ||
| − | * Verwenden Sie zur numerischen Auswertung der Q–Funktion das Interaktionsmodul [[Komplementäre Gaußsche Fehlerfunktionen]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bestimmen Sie innerhalb des vorgegebenen Rasters die optimale Grenzfrequenz hinsichtlich des Kriteriums | + | {Bestimmen Sie innerhalb des vorgegebenen Rasters die optimale Grenzfrequenz hinsichtlich des Kriteriums „ungünstigste Fehlerwahrscheinlichkeit”. |
|type="{}"} | |type="{}"} | ||
| − | $f_{ | + | $f_\text{G, opt} \cdot T \ = \ $ { 0.4 3% } |
{Welche Werte ergeben sich damit für den ungünstigsten Störabstand und die ungünstigste Fehlerwahrscheinlichkeit? | {Welche Werte ergeben sich damit für den ungünstigsten Störabstand und die ungünstigste Fehlerwahrscheinlichkeit? | ||
|type="{}"} | |type="{}"} | ||
| − | $f_{\ | + | $f_\text{G} = \text{G, opt:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ { 5.41 3% } ${\ \rm dB}$ |
| − | $ | + | $\hspace{4.07cm}p_{\rm U} \ = \ $ { 3.1 3% } $\ \rm \%$ |
| − | { | + | {Auf welchen Wert müsste man die Rauschleistungsdichte $N_0$ $($bezogen auf die Signalenergie$)$ verringern, damit $p_{\rm U}$ nicht größer ist als $10^{\rm -6}$? |
|type="{}"} | |type="{}"} | ||
| − | $N_0/E_{\rm B}$ | + | $N_0/E_{\rm B} \ = \ $ { 1.53 3% } $\ \cdot 10^{\rm -5}$ |
| − | {Geben Sie für den unter | + | {Geben Sie für den unter '''(3)''' getroffenen Annahmen eine untere und eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ an. |
|type="{}"} | |type="{}"} | ||
| − | $p_{ | + | $p_\text{ S, min}\hspace{0.02cm} \ = \ $ { 0.25 3% } $\ \cdot 10^{\rm -6}$ |
| − | $p_{ | + | $p_\text{ S, max} \ = \ $ { 1 3% } $\ \cdot 10^{\rm -6}$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Für die Optimierung genügt es , den Quotienten $\ddot{o}(T_{\rm D})/\sigma_d$ zu maximieren | + | '''(1)''' Für die Optimierung genügt es, den Quotienten $\ddot{o}(T_{\rm D})/\sigma_d$ zu maximieren: |
| + | *Dieser ist von den in der Tabelle gegebenen Werten für die Grenzfrequenz $f_{\rm G, opt} \cdot T \underline {= 0.4}$ mit $0.735/0.197 \approx 3.73$ maximal. | ||
| + | *Zum Vergleich: Für $f_{\rm G} \cdot T = 0.3$ ergibt sich aufgrund der kleineren Augenöffnung $0.192/0.094 \approx 2.04$. | ||
| + | *Für $f_{\rm G} \cdot T = 0.5$ ist der Quotient ebenfalls kleiner als beim Optimum: $1.159/0.379 \approx 3.05$. | ||
| + | *Eine noch größere Grenzfrequenz führt zu einem sehr großen Störeffektivwert, ohne dass gleichzeitig die vertikale Augenöffnung in gleicher Weise vergrößert wird. | ||
| − | |||
| − | '''(2)''' Mit dem Ergebnis aus 1) erhält man weiter: | + | '''(2)''' Mit dem Ergebnis aus '''(1)''' erhält man weiter: |
:$$\rho_{\rm U} = \left ( {3.73}/{2} \right )^2 \approx 3.48 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$\rho_{\rm U} = \left ( {3.73}/{2} \right )^2 \approx 3.48 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
10 \cdot {\rm | 10 \cdot {\rm | ||
| − | lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline { = 5.41\,{\rm dB}} | + | lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline { = 5.41\,{\rm dB}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q}\left ( |
| − | |||
{3.73}/{2} \right) \hspace{0.15cm}\underline {\approx 0.031} \hspace{0.05cm}.$$ | {3.73}/{2} \right) \hspace{0.15cm}\underline {\approx 0.031} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' Mit dem gegebenen $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 40 \ \rm dB$, also $E_{\rm B}/N_0 = 10^4$ hat sich der ungünstigste Störabstand | + | '''(3)''' Mit dem gegebenen $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 40 \ \rm dB$, also $E_{\rm B}/N_0 = 10^4$ hat sich der ungünstigste Störabstand $10 \cdot {\rm lg} \, \rho_{\rm U} \approx 5.41 \, {\rm dB}$ ergeben. |
| + | *Für die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = 10^{\rm -6}$ muss aber $10 \cdot {\rm lg} \, \rho_{\rm U} > 13.55 \, {\rm dB}$ sein. | ||
| + | *Dies erreicht man, indem man den Quotienten $E_{\rm B}/N_0$ entsprechend erhöht: | ||
:$$10 \cdot {\rm | :$$10 \cdot {\rm | ||
lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} = 40\,{\rm dB} | lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} = 40\,{\rm dB} | ||
\hspace{0.1cm}+\hspace{0.1cm}13.55\,{\rm dB} | \hspace{0.1cm}+\hspace{0.1cm}13.55\,{\rm dB} | ||
| − | \hspace{0.1cm}-\hspace{0.1cm}5.41\,{\rm dB}= 48.14\,{\rm dB} | + | \hspace{0.1cm}-\hspace{0.1cm}5.41\,{\rm dB}= 48.14\,{\rm dB}\hspace{0.3cm} |
| − | + | \Rightarrow | |
\hspace{0.3cm} {E_{\rm B}}/{N_0} = 10^{4.814}\approx 65163 | \hspace{0.3cm} {E_{\rm B}}/{N_0} = 10^{4.814}\approx 65163 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {N_0}/{E_{\rm B}}\hspace{0.15cm}\underline { = | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {N_0}/{E_{\rm B}}\hspace{0.15cm}\underline { = | ||
| Zeile 77: | Zeile 83: | ||
| − | '''(4)''' Die obere Schranke für $p_{\rm S}$ ist gleich der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U} = \underline {10^{\rm -6}}$. Die untere Schranke liegt bei $\underline {0.25 \cdot 10^{\rm -6}}$, ist also um den Faktor 4 kleiner. | + | '''(4)''' |
| + | *Die obere Schranke für $p_{\rm S}$ ist gleich der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U} = \underline {10^{\rm -6}}$. | ||
| + | *Die untere Schranke liegt bei $\underline {0.25 \cdot 10^{\rm -6}}$, ist also um den Faktor 4 kleiner. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Digitalsignalübertragung|^3.3 Kanalverzerrungen und Entzerrung^]] | [[Category:Aufgaben zu Digitalsignalübertragung|^3.3 Kanalverzerrungen und Entzerrung^]] | ||
Aktuelle Version vom 19. Juni 2022, 13:54 Uhr
Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen:
- Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_{\rm B} = s_0^2 \cdot T$.
- Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$.
- Es liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_{\rm B}$ vor.
- Der Empfängerfrequenzgang $H_{\rm E}(f)$ beinhaltet einen idealen Kanalentzerrer $H_{\rm K}^{\rm -1}(f)$ und einen Gaußtiefpass $H_{\rm G}(f)$ mit Grenzfrequenz $f_{\rm G}$ zur Rauschleistungsbegrenzung.
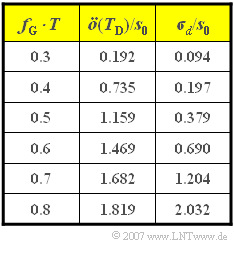
Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_{\rm D})$ sowie den Detektionsrauscheffektivwert $\sigma_{\rm d}$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_{\rm G}$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit möglichst klein ist, wobei folgende Definition gilt:
- $$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$
- Diese Größe ist eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S} \le p_{\rm U}$.
- Für $f_{\rm G} \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden: $p_{\rm S} \ge p_{\rm U}/4$.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Berücksichtigung von Kanalverzerrungen und Entzerrung".
- Verwenden Sie zur numerischen Auswertung der Q–Funktion das Interaktionsmodul Komplementäre Gaußsche Fehlerfunktionen.
Fragebogen
Musterlösung
(1) Für die Optimierung genügt es, den Quotienten $\ddot{o}(T_{\rm D})/\sigma_d$ zu maximieren:
- Dieser ist von den in der Tabelle gegebenen Werten für die Grenzfrequenz $f_{\rm G, opt} \cdot T \underline {= 0.4}$ mit $0.735/0.197 \approx 3.73$ maximal.
- Zum Vergleich: Für $f_{\rm G} \cdot T = 0.3$ ergibt sich aufgrund der kleineren Augenöffnung $0.192/0.094 \approx 2.04$.
- Für $f_{\rm G} \cdot T = 0.5$ ist der Quotient ebenfalls kleiner als beim Optimum: $1.159/0.379 \approx 3.05$.
- Eine noch größere Grenzfrequenz führt zu einem sehr großen Störeffektivwert, ohne dass gleichzeitig die vertikale Augenöffnung in gleicher Weise vergrößert wird.
(2) Mit dem Ergebnis aus (1) erhält man weiter:
- $$\rho_{\rm U} = \left ( {3.73}/{2} \right )^2 \approx 3.48 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline { = 5.41\,{\rm dB}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q}\left ( {3.73}/{2} \right) \hspace{0.15cm}\underline {\approx 0.031} \hspace{0.05cm}.$$
(3) Mit dem gegebenen $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 40 \ \rm dB$, also $E_{\rm B}/N_0 = 10^4$ hat sich der ungünstigste Störabstand $10 \cdot {\rm lg} \, \rho_{\rm U} \approx 5.41 \, {\rm dB}$ ergeben.
- Für die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = 10^{\rm -6}$ muss aber $10 \cdot {\rm lg} \, \rho_{\rm U} > 13.55 \, {\rm dB}$ sein.
- Dies erreicht man, indem man den Quotienten $E_{\rm B}/N_0$ entsprechend erhöht:
- $$10 \cdot {\rm lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} = 40\,{\rm dB} \hspace{0.1cm}+\hspace{0.1cm}13.55\,{\rm dB} \hspace{0.1cm}-\hspace{0.1cm}5.41\,{\rm dB}= 48.14\,{\rm dB}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = 10^{4.814}\approx 65163 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {N_0}/{E_{\rm B}}\hspace{0.15cm}\underline { = 1.53 \cdot 10^{-5}} \hspace{0.05cm}.$$
(4)
- Die obere Schranke für $p_{\rm S}$ ist gleich der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U} = \underline {10^{\rm -6}}$.
- Die untere Schranke liegt bei $\underline {0.25 \cdot 10^{\rm -6}}$, ist also um den Faktor 4 kleiner.