Aufgaben:Aufgabe 3.7Z: Regeneratorfeldlänge: Unterschied zwischen den Versionen
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei:P_ID1438__Dig_Z_3_7.png|right|frame|Ergebnisse einer Systemsimulation]] | [[Datei:P_ID1438__Dig_Z_3_7.png|right|frame|Ergebnisse einer Systemsimulation]] | ||
| − | Per Simulation wurde gezeigt, dass zwischen dem | + | Per Simulation wurde gezeigt, dass zwischen dem so genannten Systemwirkungsgrad $\eta$ und der charakteristischen Kabeldämpfung $a_*$ eines Koaxialkabels – beide in $\rm dB$ aufgetragen – etwa ein linearer Zusammenhang besteht, wenn die charakteristische Kabeldämpfung hinreichend groß ist $(a_* ≥ 40 \ \rm dB)$: |
:$$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} | :$$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In der Tabelle sind für vier beispielhafte Systemvarianten | + | In der Tabelle sind für vier beispielhafte Systemvarianten die empirisch gefundenen Koeffizienten $A$ und $B$ angegeben: |
| − | * | + | * für das impulsinterferenzbehaftete Binärsystem $(M = 2)$ mit Gaußtiefpass $\rm (GTP)$, siehe Kapitel <br>[[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_unter_Berücksichtigung_von_Impulsinterferenzen|Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen]], |
| − | * | + | * für das impulsinterferenzbehaftete Oktalsystem $(M = 8)$ mit Gaußtiefpass $\rm (GTP)$, siehe Kapitel <br>[[Digitalsignalübertragung/Impulsinterferenzen_bei_mehrstufiger_Übertragung|Impulsinterferenzen bei mehrstufiger Übertragung]], |
| + | *für optimale impulsinterferenzfreie Systeme $\rm (ONE)$, siehe Kapitel [[Digitalsignalübertragung/Lineare_Nyquistentzerrung|Lineare Nyquistentzerrung]]; $M = 2$ und $M = 8$. | ||
| − | + | Je größer der Systemwirkungsgrad $\eta$ ist, um so besser ist ein System für einen gegebenen Wert $a_*$ (und damit eine feste Kabellänge). | |
| − | |||
Für die Berecnung der Regeneratorfeldlänge (Abstand zweier Zwischenverstärker) ist zu beachten, dass | Für die Berecnung der Regeneratorfeldlänge (Abstand zweier Zwischenverstärker) ist zu beachten, dass | ||
| − | * die ungünstigste Fehlerwahrscheinlichkeit nicht größer sein soll als $10^{ | + | * die ungünstigste Fehlerwahrscheinlichkeit nicht größer sein soll als $10^{-10}$, woraus sich der minimale Sinkenstörabstand ergibt: |
:$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm | :$$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm | ||
dB} \hspace{0.05cm},$$ | dB} \hspace{0.05cm},$$ | ||
| − | * das logarithmierte Verhältnis von Sendeenergie (pro Bit) und AWGN–Rauschleistungsdichte ca. $100 \ \rm dB$ beträgt, zum Beispiel: | + | * das logarithmierte Verhältnis von Sendeenergie (pro Bit) und AWGN–Rauschleistungsdichte ca. $100 \ \rm dB$ beträgt, zum Beispiel: |
:$$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm | :$$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm | ||
Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$ | Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$ | ||
| Zeile 28: | Zeile 28: | ||
= 100\,{\rm | = 100\,{\rm | ||
dB} \hspace{0.05cm},$$ | dB} \hspace{0.05cm},$$ | ||
| − | * ein Normalkoaxialkabel mit den Abmessungen $2.6 \ \rm mm$ (innen) und $9.5 \ \rm mm$ (außen) eingesetzt werden soll, bei dem der folgende Zusammenhang gültig ist: | + | * ein Normalkoaxialkabel mit den Abmessungen $2.6 \ \rm mm$ (innen) und $9.5 \ \rm mm$ (außen) eingesetzt werden soll, bei dem der folgende Zusammenhang gültig ist: |
:$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | :$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | ||
MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet $a_*$ die charakteristische Dämpfung bei der halben Bitrate – im Beispiel bei $500 \ \rm MHz$ – und $l$ die Kabellänge. | + | :Hierbei bezeichnet $a_*$ die charakteristische Dämpfung bei der halben Bitrate – im Beispiel bei $500 \ \rm MHz$ – und $l$ die Kabellänge. |
| − | ''Hinweis:'' | + | |
| − | * Die Aufgabe | + | ''Hinweis:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Lineare_Nyquistentzerrung|Linare Nyquistentzerrung]]. | ||
| + | |||
| Zeile 44: | Zeile 46: | ||
{Welche der folgenden Aussagen sind zutreffend? | {Welche der folgenden Aussagen sind zutreffend? | ||
|type="[]"} | |type="[]"} | ||
| − | + Das System (ONE, | + | + Das System $({\rm ONE}, \ M = 8)$ ist für jedes beliebiges $a_*$ am besten. |
| − | - Das System (GTP, | + | - Das System $({\rm GTP}, \ M = 2)$ ist für $a_* ≥ 40 \ \rm dB$ am schlechtesten. |
| − | {Ab welcher Kabeldämpfung ist (GTP, | + | {Ab welcher Kabeldämpfung ist $({\rm GTP}, \ M = 8)$ besser als $({\rm ONE}, \ M = 2)$? |
|type="{}"} | |type="{}"} | ||
| − | $a_{\rm *, \ Grenz}$ | + | $a_{\rm *, \ Grenz}\ = \ $ { 116 3% } $\ \rm dB$ |
| − | {Welchen Minimalwert $\eta_{\rm min}$ darf der Systemwirkungsgrad | + | {Welchen Minimalwert $\eta_{\hspace{0.05cm}\rm min}$ darf der Systemwirkungsgrad auf keinen Fall unterschreiten? |
|type="{}"} | |type="{}"} | ||
| − | $10 \cdot {\rm lg} \ \eta_{\rm min}$ | + | $10 \cdot {\rm lg} \ \eta_{\hspace{0.05cm}\rm min} \ = \ $ { -86.417--81.383 } $\ \rm dB$ |
| − | {Welche Länge darf das Koaxialkabel bei (ONE, | + | {Welche Länge darf das Koaxialkabel bei $({\rm ONE}, \ M = 8)$ maximal besitzen? |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $l_{\hspace{0.05cm}\rm max}\ = \ $ { 2.62 3% } $\ \rm km$ |
| − | {Welche Länge darf das Koaxialkabel bei (GTP, | + | {Welche Länge darf das Koaxialkabel bei $({\rm GTP}, \ M = 2)$ maximal besitzen? |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $l_{\hspace{0.05cm}\rm max}\ = \ $ { 1.61 3% } $\ \rm km$ |
</quiz> | </quiz> | ||
| Zeile 67: | Zeile 69: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Berechnet man den Systemwirkungsgrad unter der Vorraussetzung $a_* = 40 \ \rm dB$, so erhält man für die vier Systemvarianten: | '''(1)''' Berechnet man den Systemwirkungsgrad unter der Vorraussetzung $a_* = 40 \ \rm dB$, so erhält man für die vier Systemvarianten: | ||
| − | :$${\rm GTP},\hspace{0.1cm}M=2 \ | + | :$$({\rm GTP},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm} 10 \cdot {\rm |
lg}\hspace{0.1cm}\eta | lg}\hspace{0.1cm}\eta | ||
= +9.4\,{\rm dB} -1.10 \cdot 40\,{\rm dB} = -34.6\,{\rm dB}\hspace{0.05cm},$$ | = +9.4\,{\rm dB} -1.10 \cdot 40\,{\rm dB} = -34.6\,{\rm dB}\hspace{0.05cm},$$ | ||
| − | :$${\rm GTP},\hspace{0.1cm}M=8 \ | + | :$$({\rm GTP},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm}10 \cdot {\rm |
lg}\hspace{0.1cm}\eta | lg}\hspace{0.1cm}\eta | ||
= -1.3\,{\rm dB} -0.91 \cdot 40\,{\rm dB} = -37.7\,{\rm dB}\hspace{0.05cm},$$ | = -1.3\,{\rm dB} -0.91 \cdot 40\,{\rm dB} = -37.7\,{\rm dB}\hspace{0.05cm},$$ | ||
| − | :$${\rm ONE},\hspace{0.1cm}M=2 \ | + | :$$({\rm ONE},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm}10 \cdot {\rm |
lg}\hspace{0.1cm}\eta | lg}\hspace{0.1cm}\eta | ||
= +4.5\,{\rm dB} -0.96 \cdot 40 \,{\rm dB}= -33.9\,{\rm dB}\hspace{0.05cm},$$ | = +4.5\,{\rm dB} -0.96 \cdot 40 \,{\rm dB}= -33.9\,{\rm dB}\hspace{0.05cm},$$ | ||
| − | :$${\rm ONE},\hspace{0.1cm}M=8 \ | + | :$$({\rm ONE},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm} 10 \cdot {\rm |
lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot 40\,{\rm dB} = -30.9\,{\rm | lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot 40\,{\rm dB} = -30.9\,{\rm | ||
dB}\hspace{0.05cm}.$$ | dB}\hspace{0.05cm}.$$ | ||
| − | Die <u>erste Aussage</u> ist zutreffend, da das System (ONE, | + | Daraus ergibt sich: |
| + | *Die <u>erste Aussage</u> ist zutreffend, da das System $({\rm ONE},\hspace{0.1cm} M = 8)$ bereits bei $40 \ \rm dB$ Kabeldämpfung am besten ist und den günstigsten $\rm B$–Koeffizienten aufweist. | ||
| + | *Dagegen trifft die zweite Aussage nicht zu, da zum Beispiel bei $40 \ \rm dB$ Kabeldämpfung das oktale $\rm GTP$–System schlechter ist als das binäre. | ||
| − | '''(2)''' Als Bestimmungsgleichung benutzen wir | + | |
| − | :$$-1.3\,{\rm dB} -0.91 \cdot a_{\star} = +4.5 \,{\rm dB}-0.96 \cdot a_{\star} | + | '''(2)''' Als Bestimmungsgleichung benutzen wir hier: |
| − | + | :$$-1.3\,{\rm dB} -0.91 \cdot a_{\star} = +4.5 \,{\rm dB}-0.96 \cdot a_{\star}\hspace{0.3cm} | |
| + | \Rightarrow \hspace{0.3cm} 0.05 \cdot a_{\star} = 5.8\,{\rm dB} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\star,\hspace{0.05cm}{\rm Grenz}} \hspace{0.15cm}\underline {= 116\,{\rm dB}}\hspace{0.05cm}.$$ | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\star,\hspace{0.05cm}{\rm Grenz}} \hspace{0.15cm}\underline {= 116\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | Das heißt: Bis zur charakteristischen Kabeldämpfung $a_* = 116 \ \rm dB$ (Anmerkung: dies ist ein unrealistisch großer Wert für realisierte Systeme) ist das binäre Nyquistsystem dem System (GTP, | + | Das heißt: |
| + | *Bis zur charakteristischen Kabeldämpfung $a_* = 116 \ \rm dB$ (Anmerkung: dies ist ein unrealistisch großer Wert für derzeit realisierte Systeme) ist das binäre Nyquistsystem dem System $({\rm GTP},\hspace{0.1cm} M = 8)$ überlegen. | ||
| + | *Erst für größere Werte als $a_{\rm *, \ Grenz} = 116 \ \rm dB$ überwiegt bei Letzterem der Vorteil $(M = 8$ und damit deutlich niedrigere Symbolrate$)$ gegenüber dem Nachteil $($oktale Entscheidung und dadurch größeres Gewicht der Impulsinterferenzen$)$. | ||
| + | |||
| Zeile 94: | Zeile 102: | ||
:$$10 \cdot {\rm lg}\hspace{0.1cm}\rho = 10 \cdot {\rm lg} | :$$10 \cdot {\rm lg}\hspace{0.1cm}\rho = 10 \cdot {\rm lg} | ||
\hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} + 10 \cdot {\rm | \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} + 10 \cdot {\rm | ||
| − | lg}\hspace{0.1cm}\eta | + | lg}\hspace{0.1cm}\eta \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta \ > | |
\ 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} - 10 \cdot {\rm | \ 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} - 10 \cdot {\rm | ||
lg} | lg} | ||
| − | \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} = | + | \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} = |
| − | + | \ 16.1- 100\hspace{0.15cm}\underline {= -83.9\,{\rm dB} = 10 \cdot {\rm | |
| − | lg}\hspace{0.1cm}\eta_{\rm min}}\hspace{0.05cm}.$$ | + | lg}\hspace{0.1cm}\eta_{\hspace{0.05cm} \rm min}}\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | Aus & | + | '''(4)''' Beim hier betrachteten System gilt: $10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot a_{\star}.$ |
| + | *Aus der Bedingung für den Systemwirkungsgrad ⇒ $10 \cdot {\rm lg} \, \eta > \hspace{0.1cm}–83.9 \ \rm dB $ ergibt sich somit die Bedingung für die charakteristische Kabeldämpfung: | ||
:$$a_{\star} < \frac{-83.9\,{\rm dB} + 9.3\,{\rm dB}} {-0.54} \approx | :$$a_{\star} < \frac{-83.9\,{\rm dB} + 9.3\,{\rm dB}} {-0.54} \approx | ||
138.1\,{\rm dB} \hspace{0.05cm}.$$ | 138.1\,{\rm dB} \hspace{0.05cm}.$$ | ||
| − | Mit der angegebenen Gleichung | + | *Mit der angegebenen Gleichung |
:$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | :$$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm | ||
MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | ist damit die maximale Kabellänge (Regeneratorfeldlänge) angebbar: | + | :ist damit die maximale Kabellänge (Regeneratorfeldlänge) angebbar: |
| − | :$$l_{\rm max} = \frac{138.1\,{\rm dB} } {2.36\,{\rm dB}/ | + | :$$l_{\rm max} = \frac{138.1\,{\rm dB} } {2.36\,{\rm dB}/{\rm |
| − | \cdot \sqrt | + | km} \cdot \sqrt{\rm MHz})\cdot \sqrt{500\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 2.62\, |
{\rm km}} \hspace{0.05cm}.$$ | {\rm km}} \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 6. März 2019, 10:35 Uhr
Per Simulation wurde gezeigt, dass zwischen dem so genannten Systemwirkungsgrad $\eta$ und der charakteristischen Kabeldämpfung $a_*$ eines Koaxialkabels – beide in $\rm dB$ aufgetragen – etwa ein linearer Zusammenhang besteht, wenn die charakteristische Kabeldämpfung hinreichend groß ist $(a_* ≥ 40 \ \rm dB)$:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} \hspace{0.05cm}.$$
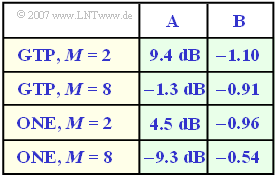
In der Tabelle sind für vier beispielhafte Systemvarianten die empirisch gefundenen Koeffizienten $A$ und $B$ angegeben:
- für das impulsinterferenzbehaftete Binärsystem $(M = 2)$ mit Gaußtiefpass $\rm (GTP)$, siehe Kapitel
Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen, - für das impulsinterferenzbehaftete Oktalsystem $(M = 8)$ mit Gaußtiefpass $\rm (GTP)$, siehe Kapitel
Impulsinterferenzen bei mehrstufiger Übertragung, - für optimale impulsinterferenzfreie Systeme $\rm (ONE)$, siehe Kapitel Lineare Nyquistentzerrung; $M = 2$ und $M = 8$.
Je größer der Systemwirkungsgrad $\eta$ ist, um so besser ist ein System für einen gegebenen Wert $a_*$ (und damit eine feste Kabellänge).
Für die Berecnung der Regeneratorfeldlänge (Abstand zweier Zwischenverstärker) ist zu beachten, dass
- die ungünstigste Fehlerwahrscheinlichkeit nicht größer sein soll als $10^{-10}$, woraus sich der minimale Sinkenstörabstand ergibt:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} \approx 16.1\,{\rm dB} \hspace{0.05cm},$$
- das logarithmierte Verhältnis von Sendeenergie (pro Bit) und AWGN–Rauschleistungsdichte ca. $100 \ \rm dB$ beträgt, zum Beispiel:
- $$s_0 = 3\,{\rm V},\hspace{0.2cm}R_{\rm B} = 1\,{\rm Gbit/s},\hspace{0.2cm}N_{\rm 0} = 9 \cdot 10^{-19}\,{\rm V^2/Hz}$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}}= 10 \cdot {\rm lg} \hspace{0.1cm} \frac{9\,{\rm V^2} } {9 \cdot 10^{-19}\,{\rm V^2/Hz} \cdot 10^{-9}\,{\rm 1/s}} = 100\,{\rm dB} \hspace{0.05cm},$$
- ein Normalkoaxialkabel mit den Abmessungen $2.6 \ \rm mm$ (innen) und $9.5 \ \rm mm$ (außen) eingesetzt werden soll, bei dem der folgende Zusammenhang gültig ist:
- $$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} \hspace{0.05cm}.$$
- Hierbei bezeichnet $a_*$ die charakteristische Dämpfung bei der halben Bitrate – im Beispiel bei $500 \ \rm MHz$ – und $l$ die Kabellänge.
Hinweis:
- Die Aufgabe gehört zum Kapitel Linare Nyquistentzerrung.
Fragebogen
Musterlösung
- $$({\rm GTP},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\eta = +9.4\,{\rm dB} -1.10 \cdot 40\,{\rm dB} = -34.6\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm GTP},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta = -1.3\,{\rm dB} -0.91 \cdot 40\,{\rm dB} = -37.7\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm ONE},\hspace{0.1cm}M=2) \text{:}\hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta = +4.5\,{\rm dB} -0.96 \cdot 40 \,{\rm dB}= -33.9\,{\rm dB}\hspace{0.05cm},$$
- $$({\rm ONE},\hspace{0.1cm}M=8) \text{:}\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot 40\,{\rm dB} = -30.9\,{\rm dB}\hspace{0.05cm}.$$
Daraus ergibt sich:
- Die erste Aussage ist zutreffend, da das System $({\rm ONE},\hspace{0.1cm} M = 8)$ bereits bei $40 \ \rm dB$ Kabeldämpfung am besten ist und den günstigsten $\rm B$–Koeffizienten aufweist.
- Dagegen trifft die zweite Aussage nicht zu, da zum Beispiel bei $40 \ \rm dB$ Kabeldämpfung das oktale $\rm GTP$–System schlechter ist als das binäre.
(2) Als Bestimmungsgleichung benutzen wir hier:
- $$-1.3\,{\rm dB} -0.91 \cdot a_{\star} = +4.5 \,{\rm dB}-0.96 \cdot a_{\star}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 0.05 \cdot a_{\star} = 5.8\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\star,\hspace{0.05cm}{\rm Grenz}} \hspace{0.15cm}\underline {= 116\,{\rm dB}}\hspace{0.05cm}.$$
Das heißt:
- Bis zur charakteristischen Kabeldämpfung $a_* = 116 \ \rm dB$ (Anmerkung: dies ist ein unrealistisch großer Wert für derzeit realisierte Systeme) ist das binäre Nyquistsystem dem System $({\rm GTP},\hspace{0.1cm} M = 8)$ überlegen.
- Erst für größere Werte als $a_{\rm *, \ Grenz} = 116 \ \rm dB$ überwiegt bei Letzterem der Vorteil $(M = 8$ und damit deutlich niedrigere Symbolrate$)$ gegenüber dem Nachteil $($oktale Entscheidung und dadurch größeres Gewicht der Impulsinterferenzen$)$.
(3) Das Sinken–SNR soll mindestens $16.1 \ \rm dB$ betragen, das heißt es muss gelten:
- $$10 \cdot {\rm lg}\hspace{0.1cm}\rho = 10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} + 10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg}\hspace{0.1cm}\eta \ > \ 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm min} - 10 \cdot {\rm lg} \hspace{0.1cm}\frac{s_0^2 }{N_0 \cdot R_{\rm B}} = \ 16.1- 100\hspace{0.15cm}\underline {= -83.9\,{\rm dB} = 10 \cdot {\rm lg}\hspace{0.1cm}\eta_{\hspace{0.05cm} \rm min}}\hspace{0.05cm}.$$
(4) Beim hier betrachteten System gilt: $10 \cdot {\rm lg}\hspace{0.1cm}\eta = -9.3\,{\rm dB} -0.54 \cdot a_{\star}.$
- Aus der Bedingung für den Systemwirkungsgrad ⇒ $10 \cdot {\rm lg} \, \eta > \hspace{0.1cm}–83.9 \ \rm dB $ ergibt sich somit die Bedingung für die charakteristische Kabeldämpfung:
- $$a_{\star} < \frac{-83.9\,{\rm dB} + 9.3\,{\rm dB}} {-0.54} \approx 138.1\,{\rm dB} \hspace{0.05cm}.$$
- Mit der angegebenen Gleichung
- $$a_{\star} = \frac{2.36\,{\rm dB} } {{\rm km} \cdot \sqrt{{\rm MHz}}} \cdot l \cdot \sqrt{{R_{\rm B}}/{2}} \hspace{0.05cm}.$$
- ist damit die maximale Kabellänge (Regeneratorfeldlänge) angebbar:
- $$l_{\rm max} = \frac{138.1\,{\rm dB} } {2.36\,{\rm dB}/{\rm km} \cdot \sqrt{\rm MHz})\cdot \sqrt{500\,{\rm MHz}}} \hspace{0.15cm}\underline {\approx 2.62\, {\rm km}} \hspace{0.05cm}.$$
(5) Nach gleichem Vorgehen, aber in kompakterer Schreibweise, ergibt sich für dieses „schlechtere” System eine kleinere Regeneratorfeldlänge:
- $$l_{\rm max} = \frac{-(83.9\,{\rm dB}+A)/B } {2.36\,{\rm dB}/{\rm km} \cdot \sqrt{500}} = \frac{+(83.9+9.4)/1.10 } {2.36\cdot \sqrt{500}}\hspace{0.1cm}{\rm km}\hspace{0.15cm}\underline {\approx 1.61\, {\rm km}} \hspace{0.05cm}.$$