Aufgaben:Aufgabe 1.7: Systemwirkungsgrade: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| − | [[Datei:P_ID1294__Dig_A_1_7.png|right|frame| | + | [[Datei:P_ID1294__Dig_A_1_7.png|right|frame|Sendegrundimpuls „Trapez” ]] |
| − | Der Empfänger eines binären Nachrichtenübertragungssystems mit Symboldauer $T$ besteht aus einem Integrator, der durch die Impulsantwort | + | Der Empfänger eines binären Nachrichtenübertragungssystems mit Symboldauer $T$ besteht aus einem Integrator, der durch die Impulsantwort |
| − | :$$ | + | :$$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ |
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
\begin{array}{*{1}c} {\rm{f\ddot{u}r}} | \begin{array}{*{1}c} {\rm{f\ddot{u}r}} | ||
| Zeile 13: | Zeile 13: | ||
|t| > T/2 \\ | |t| > T/2 \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | beschreibbar ist. Danach folgt ein Schwellenwertentscheider mit optimalen Parametern. | + | beschreibbar ist. Danach folgt ein Schwellenwertentscheider mit optimalen Parametern. |
| − | Der Sendegrundimpuls $g_{s}(t)$ gemäß der Grafik | + | Der Sendegrundimpuls $g_{s}(t)$ gemäß der Grafik sei im Allgemeinen trapezförmig und wird durch die Zeit $T_{1}$ parametrisiert: |
| + | *Für $T_{1} = 0$ ergibt sich ein Dreieckimpuls, für $T_{1} = T$ das NRZ–Rechteck. | ||
| + | *Die absolute Impulsdauer $T_{\rm S}$ ist stets gleich der Symboldauer $T$, also dem Abstand zweier Sendeimpulse. | ||
| − | Das Signal–zu–Rausch–Leistungsverhältnis (SNR) vor dem Schwellenwertentscheider kann unter der Voraussetzung, dass keine Impulsinterferenzen auftreten, wie folgt berechnet werden: | + | |
| + | Das Signal–zu–Rausch–Leistungsverhältnis $\rm (SNR)$ vor dem Schwellenwertentscheider kann unter der Voraussetzung, dass keine Impulsinterferenzen auftreten, wie folgt berechnet werden: | ||
:$$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$ | :$$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$ | ||
| − | Hierbei ist $g_{0} = g_{d}(t = 0)$ der Maximalwert des Detektionsgrundimpulses und | + | Hierbei ist $g_{0} = g_{d}(t = 0)$ der Maximalwert des Detektionsgrundimpulses und |
:$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$ | :$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$ | ||
die Rauschleistung nach dem Empfangsfilter bei AWGN–Rauschen an seinem Eingang. | die Rauschleistung nach dem Empfangsfilter bei AWGN–Rauschen an seinem Eingang. | ||
Im Laufe dieser Aufgabe werden folgende Größen verwendet: | Im Laufe dieser Aufgabe werden folgende Größen verwendet: | ||
| − | *$\rho_{d,\rm max | L}$ ist das maximale SNR unter der Nebenbedingung der Leistungsbegrenzung. | + | *$\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} L}$ ist das maximale SNR unter der Nebenbedingung der Leistungsbegrenzung. |
| − | *$\rho_{d,\rm max | A}$ ist das maximale SNR bei Spitzenwertbegrenzung (Amplitudenbegrenzung). | + | *$\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} A}$ ist das maximale SNR bei Spitzenwertbegrenzung ("Amplitudenbegrenzung"). |
Mit diesen Definitionen lassen sich die Systemwirkungsgrade angeben: | Mit diesen Definitionen lassen sich die Systemwirkungsgrade angeben: | ||
| − | :$$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0. | + | :$$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} |
L}}}\hspace{0.05cm},$$ | L}}}\hspace{0.05cm},$$ | ||
| − | :$$\eta_{\rm A} = \ \frac{\rho_d}{\rho_{d, \hspace{0. | + | :$$\eta_{\rm A} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max\hspace{0.05cm} | |
\hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$ | \hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$ | ||
| − | Hierbei bezeichnet der | + | Hierbei bezeichnet der "Crestfaktor" $C_{\rm S}$ das Verhältnis zwischen dem Maximalwert und dem Effektivwert (Wurzel aus der Leistung) des Sendesignals $s(t)$. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme|"Optimierung der Basisbandübertragungssysteme"]]. | ||
| + | |||
| + | *Verwenden Sie zur Lösung der Aufgabe folgende Zahlenwerte: | ||
| + | :$$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Berechnen Sie die Impulsenergie $E_{\rm B}$ in Abhängigkeit von $T_{1}$. Welche Werte ergeben sich für $T_{1} = 0$ , $T_{1} = T/2$ und $T_{1} = T$? | ||
| + | |type="{}"} | ||
| + | $T_{1} = 0\text{:} \hspace{0.75cm} E_{\rm B} \ = \ $ { 1 3% } $\ \cdot 10^{-8} \, \rm Ws$ | ||
| + | $T_{1} = T/2\text{:}\hspace{0.2cm} E_{\rm B} \ = \ $ { 2 3% } $\ \cdot 10^{-8} \, \rm Ws$ | ||
| + | $T_{1} = T\text{:}\hspace{0.65cm} E_{\rm B} \ = \ $ { 3 3% } $\ \cdot 10^{-8} \, \rm Ws$ | ||
| + | |||
| + | {Welcher Wert $T_{1}$ führt bei Leistungsbegrenzung zum maximal möglichen SNR? | ||
| + | |type="{}"} | ||
| + | $T_{1}/T \ = \ $ { 1 3% } | ||
| + | |||
| + | {Wie groß ist somit das maximale SNR bei Leistungsbegrenzung? | ||
| + | |type="{}"} | ||
| + | $\rho_{d,\hspace{0.05cm}\rm max \hspace{0.05cm}|\hspace{0.05cm} L} \ = \ $ { 200 3% } | ||
| + | |||
| + | {Wie groß ist der Detektionsgrundimpuls $g_{d}(t)$ in Impulsmitte für $T_{1} = T/2$? | ||
| + | |type="{}"} | ||
| + | $g_{0} \ = \ $ { 0.075 3% } $\ \rm \sqrt{W}$ | ||
| + | |||
| + | {Berechnen Sie den Systemwirkungsgrad $\eta_{\rm L}$ bei Leistungsbegrenzung $(T_{1} = T/2)$. | ||
| + | |type="{}"} | ||
| + | $\eta_{\rm L} \ = \ $ { 0.5625 3% } | ||
| + | |||
| + | {Berechnen Sie den Crestfaktor $(T_{1} = T/2)$. | ||
| + | |type="{}"} | ||
| + | $C_{\rm S} \ = \ $ { 1.225 3% } | ||
| − | { | + | {Berechnen Sie den Systemwirkungsgrad bei Spitzenwertbegrenzung $(T_{1} = T/2)$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\eta_{\rm A} \ = \ $ { 0.375 3% } |
| + | |||
| Zeile 61: | Zeile 91: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Zur Vereinfachung der Berechnungen setzen wir $T_1' = T_1/2$ und $T_2' = (T – T_1)/2$. |
| − | '''(2)''' | + | *Damit ergibt sich für die Sendeimpulsenergie: |
| − | '''(3)''' | + | :$$E_{\rm B} = |
| − | '''(4)''' | + | \int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = |
| − | '''(5)''' | + | 2 \cdot \int_{0}^{T_1\hspace{0.0cm}'}g_s^2(t) \,{\rm d} |
| − | '''(6)''' | + | t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t |
| + | \hspace{0.05cm}.$$ | ||
| + | *Entsprechend dieser Aufteilung kann auch geschrieben werden: | ||
| + | :$${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 | ||
| + | \hspace{0.05cm},\hspace{0.3cm}{\rm mit}\hspace{0.3cm} | ||
| + | E_{\rm 2} = \ | ||
| + | \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t | ||
| + | = s_0^2 \cdot \int_{0}^{T_2\hspace{0.0cm}'}\left ( 1 - \frac {t}{T_2\hspace{0.0cm}'}\right )^2 \,{\rm d} | ||
| + | t $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}E_{\rm 2} = \ s_0^2 \cdot \left [ \int_{0}^{T_2\hspace{0.0cm}'}\,\,{\rm d} t- \frac {2}{T_2\hspace{0.0cm}'} \cdot | ||
| + | \int_{0}^{T_2\hspace{0.0cm}'}t \,\,{\rm d} t + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot | ||
| + | \int_{0}^{T_2\hspace{0.0cm}'}t^2 \,\,{\rm d} t\right ] = \ s_0^2 \cdot \left [ {T_2\hspace{0.0cm}'} - \frac {2}{T_2\hspace{0.0cm}'} \cdot | ||
| + | \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^2}{2} + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot | ||
| + | \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^3}{3}\right ] = s_0^2 | ||
| + | \cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *Eingesetzt in obige Gleichung erhält man: | ||
| + | :$${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot | ||
| + | 3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} | ||
| + | \hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$ | ||
| + | *Mit den angegebenen Werten ${s_{0}}^{2} = 10 \ \rm mW$ und $T = 3\ \rm µ s$ erhält man: | ||
| + | :$$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm | ||
| + | Ws}}\hspace{0.05cm},$$ | ||
| + | :$$T_1 = T/2\text{:} \hspace{0.2cm} {E_{\rm B}} = \ 2/3 \cdot{ s_0^2 \cdot T}= \hspace{2.6cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 2 \cdot 10^{-8}\,{\rm | ||
| + | Ws}} \hspace{0.05cm},$$ | ||
| + | :$$T_1 = T\text{:} \hspace{0.65cm} {E_{\rm B}} = \ { s_0^2 \cdot T}= \hspace{3.65cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 3 \cdot 10^{-8}\,{\rm | ||
| + | Ws}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Der Systemwirkungsgrad bei Leistungsbegrenzung ist maximal $(\eta_{\rm L} = 1)$, wenn der Sendegrundimpuls $g_{s}(t)$ formgleich mit der Impulsantwort $h_{\rm E}(t)$ ist. | ||
| + | *Dies trifft hier für den NRZ–Sendeimpuls zu: $T_1/T \ \underline{= 1}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Unter der in Teilaufgabe '''(2)''' genannten Bedingung erhält man das maximale SNR: | ||
| + | :$$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} | ||
| + | L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm | ||
| + | W/Hz}}\hspace{0.1cm}\underline {= 200} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' Allgemein gilt $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$. Für $t = 0$ ergibt sich mit $T_1 = T/2$ hierfür die Trapezfläche: | ||
| + | :$$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Mit $T_1 = T/2$ (trapezförmige Sendeimpulse) erhält man für das Signal–zu–Rausch–Verhältnis: | ||
| + | :$$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} g_0^2=0.075^2\, {\rm W},\hspace{0.1cm} \sigma_d^2 = \frac{N_0}{2 \cdot T} = 5 \cdot 10^{-5}\,{\rm W}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$ | ||
| + | *Somit ergibt sich für den Systemwirkungsgrad bei Leistungsbegrenzung mit dem Ergebnis aus '''(3)''': | ||
| + | :$$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$ | ||
| + | *Aufgrund der Fehlanpassung ist $\eta_{\rm L} < 1$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Mit dem Maximalwert $s_{0}$ und dem Ergebnis der Teilaufgabe '''(1)''' gilt: | ||
| + | :$$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(7)''' Der Systemwirkungsgrad bei Spitzenwertbegrenzung ist kleiner als der bei Leistungsbegrenzung, <br> da hier neben der Fehlanpassung auch das nicht optimale Sendesignal (zu kleine Energie) eine Rolle spielt: | ||
| + | :$$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 4. Mai 2022, 13:34 Uhr
Der Empfänger eines binären Nachrichtenübertragungssystems mit Symboldauer $T$ besteht aus einem Integrator, der durch die Impulsantwort
- $$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \hspace{0.05cm}|t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \\ \end{array}$$
beschreibbar ist. Danach folgt ein Schwellenwertentscheider mit optimalen Parametern.
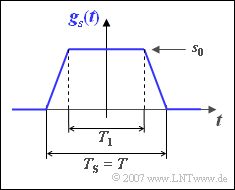
Der Sendegrundimpuls $g_{s}(t)$ gemäß der Grafik sei im Allgemeinen trapezförmig und wird durch die Zeit $T_{1}$ parametrisiert:
- Für $T_{1} = 0$ ergibt sich ein Dreieckimpuls, für $T_{1} = T$ das NRZ–Rechteck.
- Die absolute Impulsdauer $T_{\rm S}$ ist stets gleich der Symboldauer $T$, also dem Abstand zweier Sendeimpulse.
Das Signal–zu–Rausch–Leistungsverhältnis $\rm (SNR)$ vor dem Schwellenwertentscheider kann unter der Voraussetzung, dass keine Impulsinterferenzen auftreten, wie folgt berechnet werden:
- $$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$
Hierbei ist $g_{0} = g_{d}(t = 0)$ der Maximalwert des Detektionsgrundimpulses und
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$
die Rauschleistung nach dem Empfangsfilter bei AWGN–Rauschen an seinem Eingang.
Im Laufe dieser Aufgabe werden folgende Größen verwendet:
- $\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} L}$ ist das maximale SNR unter der Nebenbedingung der Leistungsbegrenzung.
- $\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} A}$ ist das maximale SNR bei Spitzenwertbegrenzung ("Amplitudenbegrenzung").
Mit diesen Definitionen lassen sich die Systemwirkungsgrade angeben:
- $$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} L}}}\hspace{0.05cm},$$
- $$\eta_{\rm A} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max\hspace{0.05cm} | \hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$
Hierbei bezeichnet der "Crestfaktor" $C_{\rm S}$ das Verhältnis zwischen dem Maximalwert und dem Effektivwert (Wurzel aus der Leistung) des Sendesignals $s(t)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Optimierung der Basisbandübertragungssysteme".
- Verwenden Sie zur Lösung der Aufgabe folgende Zahlenwerte:
- $$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- Damit ergibt sich für die Sendeimpulsenergie:
- $$E_{\rm B} = \int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = 2 \cdot \int_{0}^{T_1\hspace{0.0cm}'}g_s^2(t) \,{\rm d} t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t \hspace{0.05cm}.$$
- Entsprechend dieser Aufteilung kann auch geschrieben werden:
- $${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 \hspace{0.05cm},\hspace{0.3cm}{\rm mit}\hspace{0.3cm} E_{\rm 2} = \ \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t = s_0^2 \cdot \int_{0}^{T_2\hspace{0.0cm}'}\left ( 1 - \frac {t}{T_2\hspace{0.0cm}'}\right )^2 \,{\rm d} t $$
- $$\Rightarrow \hspace{0.3cm}E_{\rm 2} = \ s_0^2 \cdot \left [ \int_{0}^{T_2\hspace{0.0cm}'}\,\,{\rm d} t- \frac {2}{T_2\hspace{0.0cm}'} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t \,\,{\rm d} t + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t^2 \,\,{\rm d} t\right ] = \ s_0^2 \cdot \left [ {T_2\hspace{0.0cm}'} - \frac {2}{T_2\hspace{0.0cm}'} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^2}{2} + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^3}{3}\right ] = s_0^2 \cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} \hspace{0.05cm}.$$
- Eingesetzt in obige Gleichung erhält man:
- $${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot 3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} \hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$
- Mit den angegebenen Werten ${s_{0}}^{2} = 10 \ \rm mW$ und $T = 3\ \rm µ s$ erhält man:
- $$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm Ws}}\hspace{0.05cm},$$
- $$T_1 = T/2\text{:} \hspace{0.2cm} {E_{\rm B}} = \ 2/3 \cdot{ s_0^2 \cdot T}= \hspace{2.6cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 2 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm},$$
- $$T_1 = T\text{:} \hspace{0.65cm} {E_{\rm B}} = \ { s_0^2 \cdot T}= \hspace{3.65cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 3 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm}.$$
(2) Der Systemwirkungsgrad bei Leistungsbegrenzung ist maximal $(\eta_{\rm L} = 1)$, wenn der Sendegrundimpuls $g_{s}(t)$ formgleich mit der Impulsantwort $h_{\rm E}(t)$ ist.
- Dies trifft hier für den NRZ–Sendeimpuls zu: $T_1/T \ \underline{= 1}$.
(3) Unter der in Teilaufgabe (2) genannten Bedingung erhält man das maximale SNR:
- $$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm W/Hz}}\hspace{0.1cm}\underline {= 200} \hspace{0.05cm}.$$
(4) Allgemein gilt $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$. Für $t = 0$ ergibt sich mit $T_1 = T/2$ hierfür die Trapezfläche:
- $$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$
(5) Mit $T_1 = T/2$ (trapezförmige Sendeimpulse) erhält man für das Signal–zu–Rausch–Verhältnis:
- $$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} g_0^2=0.075^2\, {\rm W},\hspace{0.1cm} \sigma_d^2 = \frac{N_0}{2 \cdot T} = 5 \cdot 10^{-5}\,{\rm W}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$
- Somit ergibt sich für den Systemwirkungsgrad bei Leistungsbegrenzung mit dem Ergebnis aus (3):
- $$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$
- Aufgrund der Fehlanpassung ist $\eta_{\rm L} < 1$.
(6) Mit dem Maximalwert $s_{0}$ und dem Ergebnis der Teilaufgabe (1) gilt:
- $$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$
(7) Der Systemwirkungsgrad bei Spitzenwertbegrenzung ist kleiner als der bei Leistungsbegrenzung,
da hier neben der Fehlanpassung auch das nicht optimale Sendesignal (zu kleine Energie) eine Rolle spielt:
- $$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$