Aufgaben:Aufgabe 4.07: Nochmals Entscheidungsgrenzen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} Datei:P_ID2016__Dig_Z_4_6.png|right|frame|Drei Signalraumkon…“) |
|||
| (21 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit}} | ||
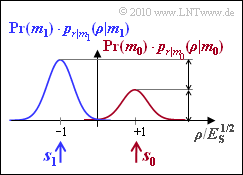
| − | [[Datei: | + | [[Datei:P_ID2017__Dig_A_4_7.png|right|frame|WDF mit ungleichen Symbolwahrscheinlichkeiten]] |
| + | Wir betrachten ein Übertragungssystem mit | ||
| + | # nur einer Basisfunktino $(N = 1)$, | ||
| + | # zwei Signalen $(M = 2)$ mit $s_0 = \sqrt{E_s}$ und $s_1 = -\sqrt{E_s}$ , | ||
| + | # einem AWGN–Kanal mit Varianz $\sigma_n^2 = N_0/2$. | ||
| + | |||
| + | |||
| + | Da in dieser Aufgabe der allgemeine Fall ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$ behandelt wird, genügt es nicht, die bedingten Dichtefunktionen $p_{\it r\hspace{0.05cm}|\hspace{0.05cm}m_i}(\rho\hspace{0.05cm} |\hspace{0.05cm}m_i)$ zu betrachten. Vielmehr müssen diese noch mit den Symbolwahrscheinlichkeiten ${\rm Pr}(m_i)$ multipliziert werden. Für $i$ sind hier die Werte $0$ und $1$ einzusetzen. | ||
| + | |||
| + | Liegt die Entscheidungsgrenze zwischen den beiden Regionen $I_0$ und $I_1$ bei $G = 0$, also in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$, so ist die Fehlerwahrscheinlichkeit unabhängig von den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$: | ||
| + | :$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Hierbei gibt $d$ den Abstand zwischen den Signalpunkten $s_0$ und $s_1$ an und $d/2$ dementsprechend den jeweiligen Abstand von $s_0$ bzw. $s_1$ von der Grenze $G = 0$. | ||
| + | |||
| + | *Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist $\sigma_n$. | ||
| + | |||
| + | |||
| + | Sind dagegen die Auftrittswahrscheinlichkeiten unterschiedlich ⇒ ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, so kann durch eine Verschiebung der Entscheidergrenze $G$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden: | ||
| + | :$$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) | ||
| + | + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$ | ||
| + | |||
| + | wobei die Hilfsgröße $\gamma$ wie folgt definiert ist: | ||
| + | :$$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} | ||
| + | \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot \sqrt {E_{\rm S}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| "Approximation der Fehlerwahrscheinlichkeit"]]. | ||
| + | |||
| + | * Die Werte der Q–Funktion können Sie mit unserem interaktiven Applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Komplementäre Gaußsche Fehlerfunktion"]] ermitteln. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie groß sind die der Grafik zugrundeliegenden Symbolwahrscheinlichkeiten, wenn die blaue Gaußkurve genau doppelt so hoch ist wie die rote? |
| − | |type=" | + | |type="{}"} |
| − | + | ${\rm Pr}(m_0)\ = \ $ { 0.333 3% } | |
| − | + | ${\rm Pr}(m_1)\ = \ $ { 0.667 3% } | |
| + | |||
| + | {Wie groß ist die Fehlerwahrscheinlichkeit mit der Rauschvarianz $\sigma_n^2 = E_{\rm S}/9$ und der '''vorgegebenen Schwelle''' $G = 0$? | ||
| + | |type="{}"} | ||
| + | $G = 0 \text{:} \hspace{0.85cm} p_{\rm S} \ = \ $ { 0.135 3% } $\ \%$ | ||
| + | |||
| + | {Wie lautet die optimale Schwelle für die gegebenen Wahrscheinlichkeiten? | ||
| + | |type="{}"} | ||
| + | $G_{\rm opt}\ = \ $ { 0.04 3% } $\ \cdot \sqrt{E_s}$ | ||
| + | |||
| + | {Wie groß ist die Fehlerwahrscheinlichkeit bei '''optimaler Schwelle''' $G = G_{\rm opt}$? | ||
| + | |type="{}"} | ||
| + | $G = G_{\rm opt} \text{:} \hspace{0.2cm} p_{\rm S}\ = \ $ { 0.126 3% } $\ \%$ | ||
| − | { | + | {Welche Fehlerwahrscheinlichkeiten erhält man mit der Rauschvarianz $\sigma_n^2 = E_{\rm S}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $G = 0 \text{:} \hspace{0.85cm} p_{\rm S}\ = \ $ { 15.9 3% } $\ \%$ |
| + | $G = G_{\rm opt} \text{:} \hspace{0.2cm} p_{\rm S}\ = \ $ { 14.5 3% } $\ \%$ | ||
| + | |||
| + | {Welche Aussagen gelten für die Rauschvarianz $\sigma_n^2 = 4 \cdot E_{\rm S}$? | ||
| + | |type="[]"} | ||
| + | + Mit $G = 0$ ist die Fehlerwahrscheinlichkeit größer als $30\%$. | ||
| + | + Die optimale Entscheiderschwelle liegt rechts von $s_0$. | ||
| + | + Bei optimaler Schwelle ist die Fehlerwahrscheinlichkeit etwa $27\%$. | ||
| + | + Der Schätzwert $m_0$ ist nur mit genügend großem Rauschen möglich. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Die Höhen der beiden gezeichneten Dichtefunktionen sind proportional zu den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$. Aus |
| + | :$${\rm Pr}(m_1) = 2 \cdot {\rm Pr}(m_0) \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$$ | ||
| + | |||
| + | :folgt direkt ${\rm Pr}(m_0) = 1/3 \ \underline {\approx 0.333}$ und ${\rm Pr}(m_1) = 2/3 \ \underline {\approx 0.667}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Mit der Entscheidergrenze $G = 0$ gilt unabhängig von den Auftrittswahrscheinlichkeiten: | ||
| + | :$$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Mit $d = 2 \cdot \sqrt{E_{\rm S}}$ und $\sigma_n = \sqrt{E_{\rm S}}/3$ ergibt sich hierfür: | ||
| + | :$$p_{\rm S} = {\rm Q} (3) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.135 \%} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Entsprechend der Angabe gilt für den „normierten Schwellenwert”: | ||
| + | :$$\gamma = \frac{G_{\rm opt}}{E_{\rm S}^{1/2}} = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} | ||
| + | = \frac{ 2 \cdot E_{\rm S}/9}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.04} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Damit ist $G_{\rm opt} = \gamma \cdot \sqrt{E_{\rm S}} = 0.04 \cdot \sqrt{E_{\rm S}}$. | ||
| + | |||
| + | *Die optimale Entscheidergrenze ist demnach nach rechts $($hin zum unwahrscheinlicheren Symbol $s_0)$ verschoben, wegen ${\rm Pr}(m_0) < {\rm Pr}(m_1)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Mit dieser optimalen Entscheidergrenze ergibt sich eine gegenüber der Teilaufgabe '''(2)''' geringfügig kleinere Fehlerwahrscheinlichkeit: | ||
| + | :$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (3 \cdot 1.04) + {1}/{3} \cdot {\rm Q} (3 \cdot 0.96) = {2}/{3} \cdot 0.090 \cdot 10^{-2} + {1}/{3} \cdot 0.199 \cdot 10^{-2} | ||
| + | \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.126 \%} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Mit der Entscheidergrenze in der Mitte zwischen den Symbolen $(G = 0)$ ergibt sich analog zur Teilaufgabe '''(2)''' mit der nun größeren Rauschvarianz: | ||
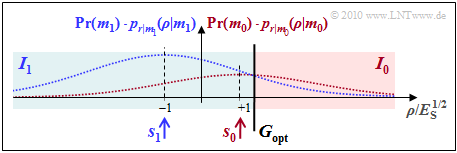
| + | [[Datei:P_ID2035__Dig_A_4_7e.png|right|frame|Wahrscheinlichkeitsdichtefunktionen mit $\sigma_n^2 = E_{\rm S}$]] | ||
| + | |||
| + | :$$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) = {\rm Q} \left ( \frac{\sqrt{E_{\rm S}}}{\sqrt{E_{\rm S}}} \right )= | ||
| + | {\rm Q} (1)\hspace{0.1cm} \hspace{0.15cm}\underline {\approx 15.9 \%} \hspace{0.05cm}.$$ | ||
| + | *Die Kenngröße $\gamma$ (normierte bestmögliche Verschiebung der Entscheidergrenze) ist | ||
| + | :$$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} | ||
| + | = \frac{ 2 \cdot E_{\rm S}}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} = \frac{{\rm ln} \hspace{0.15cm} 2}{2} \approx 0.35 $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G_{\rm opt} = 0.35 \cdot \sqrt{E_{\rm S}} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | + | *Das häufigere Symbol wird nun seltener verfälscht ⇒ die mittlere Fehlerwahrscheinlichkeit wird geringer: | |
| + | :$$p_{\rm S} = {2}/{3} \cdot {\rm Q} (1.35) + {1}/{3} \cdot {\rm Q} (0.65) = {2}/{3} \cdot 0.0885 +{1}/{3} \cdot 0.258 | ||
| + | \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 14.5 \%} \hspace{0.05cm}.$$ | ||
| + | *Die Abbildung macht deutlich, dass die optimale Entscheidergrenze auch grafisch als Schnittpunkt der beiden (gewichteten) Wahrscheinlichkeitsdichtefunktionen ermittelt werden kann: | ||
| − | |||
| + | '''(6)''' <u>Alle Lösungsvorschläge</u> dieser eher akademischen Teilaufgabe <u>sind richtig</u>: | ||
| + | [[Datei:P_ID2036__Dig_A_4_7f_version2.png|right|frame|Wahrscheinlichkeitsdichtefunktionen mit $\sigma_n^2 = 4 \cdot E_{\rm S}$]] | ||
| + | *Mit dem Schwellenwert $G = 0$ ergibt sich $p_{\rm S} = {\rm Q}(0.5) \ \underline {\approx 0.309}$. | ||
| + | *Die Kenngröße $\gamma = 1.4$ hat nun den vierfachen Wert gegenüber der Teilaufgabe '''(5)''', <br>so dass die optimale Entscheidergrenze nun bei $G_{\rm opt} = \underline {1.4 \cdot s_0}$ liegt. | ||
| + | *Somit gehört der (ungestörte) Signalwert $s_0$ nicht zur Entscheidungsregion $I_0$, sondern zu $I_1$, gekennzeichnet durch $\rho < G_{\rm opt}$. | ||
| + | *Nur mit einem (positiven) Rauschanteil ist $I_0\ (\rho > G_{\rm opt})$ überhaupt erst möglich. Für die Fehlerwahrscheinlichkeit gilt mit $G_{\rm opt} = 1.4 \cdot s_0$: | ||
| + | :$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (0.5 \cdot (1 + 1.4)) + {1}/{3} \cdot {\rm Q} (0.5 \cdot (1 - 1.4)) = | ||
| + | \hspace{0.15cm}\underline {\approx 27\%} \hspace{0.05cm}.$$ | ||
| − | + | Die nebenstehende Grafik verdeutlicht die hier gemachten Aussagen. | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 28. Juli 2022, 15:44 Uhr
Wir betrachten ein Übertragungssystem mit
- nur einer Basisfunktino $(N = 1)$,
- zwei Signalen $(M = 2)$ mit $s_0 = \sqrt{E_s}$ und $s_1 = -\sqrt{E_s}$ ,
- einem AWGN–Kanal mit Varianz $\sigma_n^2 = N_0/2$.
Da in dieser Aufgabe der allgemeine Fall ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$ behandelt wird, genügt es nicht, die bedingten Dichtefunktionen $p_{\it r\hspace{0.05cm}|\hspace{0.05cm}m_i}(\rho\hspace{0.05cm} |\hspace{0.05cm}m_i)$ zu betrachten. Vielmehr müssen diese noch mit den Symbolwahrscheinlichkeiten ${\rm Pr}(m_i)$ multipliziert werden. Für $i$ sind hier die Werte $0$ und $1$ einzusetzen.
Liegt die Entscheidungsgrenze zwischen den beiden Regionen $I_0$ und $I_1$ bei $G = 0$, also in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$, so ist die Fehlerwahrscheinlichkeit unabhängig von den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$
- Hierbei gibt $d$ den Abstand zwischen den Signalpunkten $s_0$ und $s_1$ an und $d/2$ dementsprechend den jeweiligen Abstand von $s_0$ bzw. $s_1$ von der Grenze $G = 0$.
- Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist $\sigma_n$.
Sind dagegen die Auftrittswahrscheinlichkeiten unterschiedlich ⇒ ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, so kann durch eine Verschiebung der Entscheidergrenze $G$ eine kleinere Fehlerwahrscheinlichkeit erzielt werden:
- $$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$
wobei die Hilfsgröße $\gamma$ wie folgt definiert ist:
- $$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot \sqrt {E_{\rm S}}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Approximation der Fehlerwahrscheinlichkeit".
- Die Werte der Q–Funktion können Sie mit unserem interaktiven Applet "Komplementäre Gaußsche Fehlerfunktion" ermitteln.
Fragebogen
Musterlösung
- $${\rm Pr}(m_1) = 2 \cdot {\rm Pr}(m_0) \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$$
- folgt direkt ${\rm Pr}(m_0) = 1/3 \ \underline {\approx 0.333}$ und ${\rm Pr}(m_1) = 2/3 \ \underline {\approx 0.667}$.
(2) Mit der Entscheidergrenze $G = 0$ gilt unabhängig von den Auftrittswahrscheinlichkeiten:
- $$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$
- Mit $d = 2 \cdot \sqrt{E_{\rm S}}$ und $\sigma_n = \sqrt{E_{\rm S}}/3$ ergibt sich hierfür:
- $$p_{\rm S} = {\rm Q} (3) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.135 \%} \hspace{0.05cm}.$$
(3) Entsprechend der Angabe gilt für den „normierten Schwellenwert”:
- $$\gamma = \frac{G_{\rm opt}}{E_{\rm S}^{1/2}} = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}/9}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.04} \hspace{0.05cm}.$$
- Damit ist $G_{\rm opt} = \gamma \cdot \sqrt{E_{\rm S}} = 0.04 \cdot \sqrt{E_{\rm S}}$.
- Die optimale Entscheidergrenze ist demnach nach rechts $($hin zum unwahrscheinlicheren Symbol $s_0)$ verschoben, wegen ${\rm Pr}(m_0) < {\rm Pr}(m_1)$.
(4) Mit dieser optimalen Entscheidergrenze ergibt sich eine gegenüber der Teilaufgabe (2) geringfügig kleinere Fehlerwahrscheinlichkeit:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (3 \cdot 1.04) + {1}/{3} \cdot {\rm Q} (3 \cdot 0.96) = {2}/{3} \cdot 0.090 \cdot 10^{-2} + {1}/{3} \cdot 0.199 \cdot 10^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.126 \%} \hspace{0.05cm}.$$
(5) Mit der Entscheidergrenze in der Mitte zwischen den Symbolen $(G = 0)$ ergibt sich analog zur Teilaufgabe (2) mit der nun größeren Rauschvarianz:
- $$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) = {\rm Q} \left ( \frac{\sqrt{E_{\rm S}}}{\sqrt{E_{\rm S}}} \right )= {\rm Q} (1)\hspace{0.1cm} \hspace{0.15cm}\underline {\approx 15.9 \%} \hspace{0.05cm}.$$
- Die Kenngröße $\gamma$ (normierte bestmögliche Verschiebung der Entscheidergrenze) ist
- $$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} = \frac{{\rm ln} \hspace{0.15cm} 2}{2} \approx 0.35 $$
- $$\Rightarrow \hspace{0.3cm} G_{\rm opt} = 0.35 \cdot \sqrt{E_{\rm S}} \hspace{0.05cm}.$$
- Das häufigere Symbol wird nun seltener verfälscht ⇒ die mittlere Fehlerwahrscheinlichkeit wird geringer:
- $$p_{\rm S} = {2}/{3} \cdot {\rm Q} (1.35) + {1}/{3} \cdot {\rm Q} (0.65) = {2}/{3} \cdot 0.0885 +{1}/{3} \cdot 0.258 \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 14.5 \%} \hspace{0.05cm}.$$
- Die Abbildung macht deutlich, dass die optimale Entscheidergrenze auch grafisch als Schnittpunkt der beiden (gewichteten) Wahrscheinlichkeitsdichtefunktionen ermittelt werden kann:
(6) Alle Lösungsvorschläge dieser eher akademischen Teilaufgabe sind richtig:
- Mit dem Schwellenwert $G = 0$ ergibt sich $p_{\rm S} = {\rm Q}(0.5) \ \underline {\approx 0.309}$.
- Die Kenngröße $\gamma = 1.4$ hat nun den vierfachen Wert gegenüber der Teilaufgabe (5),
so dass die optimale Entscheidergrenze nun bei $G_{\rm opt} = \underline {1.4 \cdot s_0}$ liegt. - Somit gehört der (ungestörte) Signalwert $s_0$ nicht zur Entscheidungsregion $I_0$, sondern zu $I_1$, gekennzeichnet durch $\rho < G_{\rm opt}$.
- Nur mit einem (positiven) Rauschanteil ist $I_0\ (\rho > G_{\rm opt})$ überhaupt erst möglich. Für die Fehlerwahrscheinlichkeit gilt mit $G_{\rm opt} = 1.4 \cdot s_0$:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (0.5 \cdot (1 + 1.4)) + {1}/{3} \cdot {\rm Q} (0.5 \cdot (1 - 1.4)) = \hspace{0.15cm}\underline {\approx 27\%} \hspace{0.05cm}.$$
Die nebenstehende Grafik verdeutlicht die hier gemachten Aussagen.