Aufgaben:Aufgabe 3.7: Vergleich zweier Faltungscodierer: Unterschied zwischen den Versionen
Aus LNTwww
Wael (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple…“) |
|||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm | + | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} |
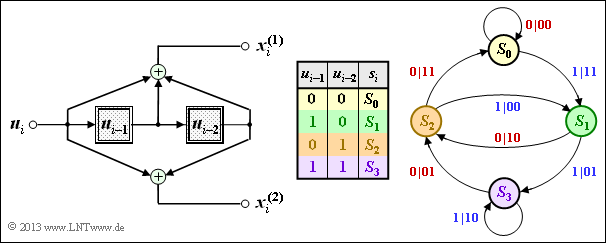
| + | [[Datei:P_ID2672__KC_A_3_7.png|right|frame|Zwei Faltungscodierer mit den Parametern $n = 2, \ k = 1, \ m = 2$]] | ||
| + | Die Grafik zeigt zwei Rate–$1/2$–Faltungscodierer, jeweils mit dem Gedächtnis $m = 2$: | ||
| + | * Der Coder $\rm A$ weist die Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$ auf. | ||
| + | * Beim Coder $\rm B$ sind die beiden Filter (oben und unten) vertauscht, und es gilt : $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$. | ||
| + | Der untere Coder $\rm B$ wurde im Theorieteil schon ausführlich behandelt. | ||
| + | In der vorliegenden Aufgabe sollen Sie zunächst das Zustandsübergangsdiagramm für Coder $\rm A$ ermitteln und anschließend die Unterschiede und die Gemeinsamkeiten zwischen den beiden Zustandsdiagrammen herausarbeiten. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Hinweise:'' | |
| − | | | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]]. |
| − | + | *Bezug genommen wird insbesondere auf die Abschnitte | |
| + | ** [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister|Zustandsdefinition für ein Speicherregister]] sowie | ||
| + | ** [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Darstellung im_Zustands.C3.BCbergangsdiagramm|Darstellung im Zustandsübergangsdiagramm]]. | ||
| + | ===Fragebogen=== | ||
| + | <quiz display=simple> | ||
| + | {Es gelte $\underline{u} = (0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. Welche Sequenzen erzeugt Coder $\rm A$? | ||
| + | |type="[]"} | ||
| + | + $\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$, | ||
| + | - $\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$, | ||
| + | - $\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$, | ||
| + | + $\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$. | ||
| + | {Welche der genannten Zustandsübergänge gibt es bei Coder $\rm A$? | ||
| + | |type="[]"} | ||
| + | + $s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$. | ||
| + | + $s_i = S_1, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_1, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$. | ||
| + | + $s_i = S_2, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_2, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$. | ||
| + | + $s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$. | ||
| + | |||
| + | {Wie unterscheiden sich die beiden Zustandsübergangsdiagramme? | ||
| + | |type="[]"} | ||
| + | - Es sind andere Zustandsübergänge möglich. | ||
| + | - Bei allen acht Übergängen stehen andere Codesequenzen. | ||
| + | + Unterschiede gibt es nur für die Codesequenzen $(01)$ und $(10)$. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | [[Datei:P_ID2673__KC_A_3_7a_neu.png|right|frame|Berechnung der Codesequenz]] |
| − | + | '''(1)''' Die Berechnung basiert auf den Gleichungen | |
| − | + | :$$x_i^{(1)} = u_i + u_{i–2},$$ | |
| − | + | :$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$ | |
| − | + | *Zu Beginn sind die beiden Speicher ($u_{i–1}$ und $u_{i–2}$) mit Nullen vorbelegt ⇒ $s_1 = S_0$. | |
| − | + | *Mit $u_1 = 0$ ergibt sich $\underline{x}_1 = (00)$ und $s_2 = S_0$. | |
| − | + | *Mit $u_2 = 1$ erhält man die Ausgabe $\underline{x}_2 = (11)$ und den neuen Zustand $s_3 = S_3$. | |
| − | + | ||
| + | |||
| + | Aus nebenstehendem Berechnungsschema erkennt man die Richtigkeit der <u>Lösungsvorschläge 1 und 4</u>. | ||
| − | [[ | + | [[Datei:P_ID2674__KC_A_3_7b.png|right|frame|Zustandsübergangsdiagramm von Coder $\rm A$]] |
| + | '''(2)''' <u>Alle Lösungsvorschläge</u> sind richtig: | ||
| + | *Dies erkennt man durch Auswertung der Tabelle bei '''(1)'''. | ||
| + | *Die Ergebnisse sind in nebenstehender Grafik dargestellt. | ||
| + | <br clear=all> | ||
| + | [[Datei:P_ID2675__KC_A_3_7c.png|right|frame|Zustandsübergangsdiagramm von Coder $\rm B$]] | ||
| + | '''(3)''' Richtig ist nur die <u>Aussage 3</u>: | ||
| + | *Rechts ist das Zustandsübergangsdiagramm von Coder $\rm B$ skizziert. Herleitung und Tnterpretation siehe Abschnitt [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Darstellung im_Zustands.C3.BCbergangsdiagramm|Darstellung im Zustandsübergangsdiagramm]]. | ||
| + | *Vertauscht man die beiden Ausgabebits $x_i^{(1)}$ und $x_i^{(2)}$, so kommt man vom Faltungscodierer $\rm A$ zum Faltungscodierer $\rm B$ (und umgekehrt). | ||
| + | {{ML-Fuß}} | ||
| − | ^]] | + | [[Category:Aufgaben zu Kanalcodierung|^3.3 Zustands– und Trellisdiagramm^]] |
Aktuelle Version vom 7. Juni 2019, 15:10 Uhr
Die Grafik zeigt zwei Rate–$1/2$–Faltungscodierer, jeweils mit dem Gedächtnis $m = 2$:
- Der Coder $\rm A$ weist die Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$ auf.
- Beim Coder $\rm B$ sind die beiden Filter (oben und unten) vertauscht, und es gilt : $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$.
Der untere Coder $\rm B$ wurde im Theorieteil schon ausführlich behandelt.
In der vorliegenden Aufgabe sollen Sie zunächst das Zustandsübergangsdiagramm für Coder $\rm A$ ermitteln und anschließend die Unterschiede und die Gemeinsamkeiten zwischen den beiden Zustandsdiagrammen herausarbeiten.
Hinweise:
- Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.
- Bezug genommen wird insbesondere auf die Abschnitte
Fragebogen
Musterlösung
(1) Die Berechnung basiert auf den Gleichungen
- $$x_i^{(1)} = u_i + u_{i–2},$$
- $$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$
- Zu Beginn sind die beiden Speicher ($u_{i–1}$ und $u_{i–2}$) mit Nullen vorbelegt ⇒ $s_1 = S_0$.
- Mit $u_1 = 0$ ergibt sich $\underline{x}_1 = (00)$ und $s_2 = S_0$.
- Mit $u_2 = 1$ erhält man die Ausgabe $\underline{x}_2 = (11)$ und den neuen Zustand $s_3 = S_3$.
Aus nebenstehendem Berechnungsschema erkennt man die Richtigkeit der Lösungsvorschläge 1 und 4.
(2) Alle Lösungsvorschläge sind richtig:
- Dies erkennt man durch Auswertung der Tabelle bei (1).
- Die Ergebnisse sind in nebenstehender Grafik dargestellt.
(3) Richtig ist nur die Aussage 3:
- Rechts ist das Zustandsübergangsdiagramm von Coder $\rm B$ skizziert. Herleitung und Tnterpretation siehe Abschnitt Darstellung im Zustandsübergangsdiagramm.
- Vertauscht man die beiden Ausgabebits $x_i^{(1)}$ und $x_i^{(2)}$, so kommt man vom Faltungscodierer $\rm A$ zum Faltungscodierer $\rm B$ (und umgekehrt).