Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm: Unterschied zwischen den Versionen
| (32 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| − | == Zustandsdefinition für ein Speicherregister | + | == Zustandsdefinition für ein Speicherregister == |
<br> | <br> | ||
| − | Ein Faltungscodierer kann auch als Automat mit endlicher Anzahl von Zuständen aufgefasst werden. Die Zustandsanzahl ergibt sich | + | Ein Faltungscodierer kann auch als Automat mit endlicher Anzahl von Zuständen aufgefasst werden. Die Zustandsanzahl ergibt sich aus der Zahl der Speicherelemente ⇒ Gedächtnis $m$ dabei zu $2^m$.<br> |
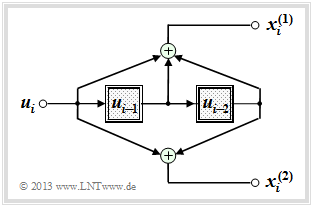
| − | [[Datei:P ID2630 KC T 3 3 S1 v2.png|Faltungscodierer mit | + | [[Datei:P ID2630 KC T 3 3 S1 v2.png|right|frame|Faltungscodierer mit $k = 1, \ n = 2, \ m = 2$|class=fit]] |
| − | + | In diesem Kapitel gehen wir meist vom gezeichneten Faltungscodierer aus, der durch folgende Kenngrößen charakterisiert wird: | |
| − | *$k = 1, \ n = 2$ ⇒ Coderate $R = 1/2$,<br> | + | *$k = 1, \ n = 2$ ⇒ Coderate $R = 1/2$,<br> |
| − | *Gedächtnis $m = 2$ ⇒ Einflusslänge $\nu = 3$,<br> | + | *Gedächtnis $m = 2$ ⇒ Einflusslänge $\nu = 3$,<br> |
| − | *Übertragungsfunktionsmatrix in Oktalform $(7, 5)$ | + | *Übertragungsfunktionsmatrix in Oktalform $(7, 5)$: |
| + | :$$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$ | ||
| − | Die Codesequenz zum Zeitpunkt $i$ ⇒ $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ hängt außer vom Informationsbit $u_i$ auch vom Inhalt $(u_{i | + | Die Codesequenz zum Zeitpunkt $i$ ⇒ $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ hängt außer vom Informationsbit $u_i$ auch vom Inhalt $(u_{i-1}, \ u_{i-2})$ des Speichers ab. |
| + | *Hierfür gibt es $2^m = 4$ Möglichkeiten, nämlich die Zustände $S_0, \ S_1, \ S_2$ und $S_3$. | ||
| + | *Der Registerzustand $S_{\mu}$ sei dabei über den Index definiert: | ||
| − | :<math>\mu = u_{i-1} + 2 \cdot u_{i-2}\hspace{0.05cm}, \hspace{0.5cm}{\rm allgemein\hspace{-0.1cm}:}\hspace{0.15cm} | + | ::<math>\mu = u_{i-1} + 2 \cdot u_{i-2}\hspace{0.05cm}, \hspace{0.5cm}{\rm allgemein\hspace{-0.1cm}:}\hspace{0.15cm} |
\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} | \mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Im Englischen verwendet man für „Zustand” den Begriff | + | Im Englischen verwendet man für „Zustand” den Begriff „State”. Deshalb ist auch im deutschen Text manchmal vom <i>Registerstatus</i> die Rede.<br> |
Um Verwechslungen zu vermeiden, unterscheiden wir im Weiteren durch Groß– bzw. Kleinbuchstaben: | Um Verwechslungen zu vermeiden, unterscheiden wir im Weiteren durch Groß– bzw. Kleinbuchstaben: | ||
| − | *die möglichen Zustände $S_{\mu}$ mit den Indizes $0 ≤ \mu ≤ 2^m \, | + | *die möglichen Zustände $S_{\mu}$ mit den Indizes $0 ≤ \mu ≤ 2^m \,-1$,<br> |
| − | *die aktuellen Zustände $s_i$ zu den Zeitpunkten $i = 1, \ 2, \ 3, \ ...$ | + | *die aktuellen Zustände $s_i$ zu den Zeitpunkten $i = 1, \ 2, \ 3, \ \text{...}$<br> |
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 1:}$ Die Grafik zeigt für den oben skizzierten Faltungscodierer | |
| − | + | *die Informationssequenz $\underline{u} = (u_1,u_2, \text{...} \ ) $ ⇒ Informationsbits $u_i$, | |
| − | * | + | |
| + | *die aktuellen Zustände zu den Zeitpunkten $i$ ⇒ $s_i ∈ \{S_0, \ S_1, \ S_2, \ S_3\}$,<br> | ||
| + | |||
| + | *die 2 Bit–Sequenzen $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ ⇒ Codierung des Informationsbits $u_i$.<br> | ||
| − | |||
| − | + | [[Datei:P ID2631 KC T 3 3 S1b v1.png|center|frame|Zur Verdeutlichung der Registerzustände $S_{\mu}$|class=fit]] | |
| − | + | Beispielsweise erkennt man aus dieser Darstellung (die Farben sollen den Übergang zu späteren Grafiken erleichtern): | |
| − | + | *Zum Zeitpunkt $i = 5$ gilt $u_{i-1} = u_4 = 0$, $u_{i-2} = u_3 = 1$. Das heißt, der Automat befindet sich im Zustand $s_5 = S_2$. Mit dem Informationsbit $u_i = u_5 = 0$ erhält man die Codesequenz $\underline{x}_5 = (11)$.<br> | |
| − | *Zum Zeitpunkt $i = 5$ gilt $u_{i | ||
| − | *Der Zustand für den Zeitpunkt $i = 6$ ergibt sich aus $u_{i | + | *Der Zustand für den Zeitpunkt $i = 6$ ergibt sich aus $u_{i-1} = u_5 = 0$ und $u_{i-2} = u_4 = 0$ zu $s_6 = S_0$. Wegen $u_6 = 0$ wird nun $\underline{x}_6 = (00)$ ausgegeben und der neue Zustand $s_7$ ist wiederum $S_0$.<br> |
| − | * | + | *Zum Zeitpunkt $i = 12$ wird wegen $u_{12} = 0$ wie zum Zeitpunkt $i = 5$ die Codesequenz $\underline{x}_{12} = (11)$ ausgegeben und man geht vom Zustand $s_{12} = S_2$ in den Zustand $s_{13} = S_0$ über.<br> |
| − | *Dagegen wird zum Zeitpunkt $i = 9$ die Codesequenz $(00)$ ausgegeben und auf $s_9 = S_2$ folgt $s_{10} = S_1$. Gleiches gilt auch für $i = 15$. In beiden Fällen lautet das aktuelle Informationsbit $u_i = 1$. | + | *Dagegen wird zum Zeitpunkt $i = 9$ die Codesequenz $\underline{x}_{9} = (00)$ ausgegeben und auf $s_9 = S_2$ folgt $s_{10} = S_1$. Gleiches gilt auch für $i = 15$. In beiden Fällen lautet das aktuelle Informationsbit $u_i = 1$.}}<br> |
| − | Aus diesem Beispiel ist zu erkennen, dass die Codesequenz $\underline{x}_i$ zum Zeitpunkt $i$ allein | + | {{BlaueBox|TEXT= |
| − | *vom aktuellen Zustand $s_i = S_{\mu} (0 ≤ \mu ≤ 2^m | + | $\text{Fazit:}$ Aus diesem Beispiel ist zu erkennen, dass die Codesequenz $\underline{x}_i$ zum Zeitpunkt $i$ allein abhängt |
| + | *vom aktuellen Zustand $s_i = S_{\mu} \ \ (0 ≤ \mu ≤ 2^m -1)$, sowie<br> | ||
| + | *vom aktuellen Informationsbit $u_i$.<br><br> | ||
| − | + | Ebenso wird der Nachfolgezustand $s_{i+1}$ allein durch $s_i$ und $u_i$ bestimmt. | |
| − | + | Diese Eigenschaften werden im so genannten <i>Zustandsübergangsdiagramm</i> auf der nächsten Seite berücksichtigt.}}<br> | |
| − | == Darstellung im Zustandsübergangsdiagramm | + | == Darstellung im Zustandsübergangsdiagramm == |
<br> | <br> | ||
| − | Die Grafik zeigt das <b>Zustandsübergangsdiagramm</b> (englisch: <i>State Transition Diagram</i>) für unseren | + | Die Grafik zeigt das <b>Zustandsübergangsdiagramm</b> (englisch: <i>State Transition Diagram</i> ) für unseren '''„Standard–Codierer”'''. |
| + | *Dieses liefert alle Informationen über den $(n = 2, \ k = 1, \ m = 2)$–Faltungscodierer in kompakter Form. | ||
| + | *Die Farbgebung ist mit der [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister| sequenziellen Darstellung]] auf der vorherigen Seite abgestimmt. | ||
| + | *Der Vollständigkeit halber ist auch die Herleitungstabelle nochmals angegeben.<br> | ||
| − | |||
| − | + | [[Datei:P ID3022 KC T 3 3 S2 v2.png|center|frame|Zustandsübertragungsdiagramm $\rm A$ für $n = 2, \ k = 1, \ m = 2$|class=fit]] | |
| − | |||
| − | * | + | Die $2^{m+k}$ Übergänge sind mit „$u_i \ | \ \underline{x}_i$” beschriftet. Beispielsweise ist abzulesen: |
| + | *Durch das Informationsbit $u_i = 0$ (gekennzeichnet durch eine rote Beschriftung) gelangt man vom Zustand $s_i = S_1$ zum Zustand $s_{i+1} = S_2$ und die beiden Codebits lauten $x_i^{(1)} = 1, \ x_i^{(2)} = 0$.<br> | ||
| − | + | *Mit dem Informationsbit $u_i = 1$ (blaue Beschriftung) im Zustand $s_i = S_1$ ergeben sich dagegen die Codebits zu $x_i^{(1)} = 0, \ x_i^{(2)} = 1$, und man kommt zum neuen Zustand $s_{i+1} = S_3$.<br><br> | |
| − | |||
| − | + | Betrachten wir nun einen weiteren systematischen Code, ebenfalls mit den Kenngrößen $n = 2, \ k = 1, \ m = 2$. Es handelt sich hierbei um die [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#.C3.84quivalenter_systematischer_Faltungscode|äquivalente systematische Repräsentation]] des oberen Codierers. Man bezeichnet diesen auch als '''RSC–Codierer''' (englisch: <i>Recursive Systematic Convolutional Encoder</i>).<br> | |
| − | + | [[Datei:P ID2680 KC T 3 3 S2b v3.png|center|frame|Zustandsübertragungsdiagramm $\rm B$ für $n = 2, \ k = 1, \ m = 2$|class=fit]] | |
| − | + | Gegenüber dem oberen Zustandsübergangsdiagramm erkennt man folgende Unterschiede: | |
| − | + | *Da die früheren Informationsbits $u_{i-1}$ und $u_{i-2}$ nicht abgespeichert werden, beziehen sich hier die Zustände $s_i = S_{\mu}$ auf die verarbeiteten Größen $w_{i-1}$ und $w_{i-2}$, wobei $w_i = u_i + w_{i-1} + w_{i-2}$ gilt.<br> | |
| − | |||
| − | [[ | + | *Da dieser Code ebenfalls systematisch ist, gilt wieder $x_i^{(1)} = u_i$. Die Herleitung der zweiten Codebits $x_i^{(2)}$ finden Sie in der [[Aufgaben:3.5_Rekursive_Filter_f%C3%BCr_GF(2)|Aufgabe 3.5]]. Es handelt sich um ein rekursives Filter, wie im Abschnitt [[Kanalcodierung/Algebraische_und_polynomische_Beschreibung#Filterstruktur_bei_gebrochen.E2.80.93rationaler_.C3.9Cbertragungsfunktion| Filterstruktur bei gebrochen–rationaler Übertragungsfunktion]] beschrieben.<br><br> |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Fazit:}$ Der Bildervergleich zeigt, dass sich für beide Codierer ein ähnliches Zustandsübergangsdiagramm ergibt: | ||
| − | + | *Die Struktur des Zustandsübergangsdiagramms ist allein durch die Parameter $m$ und $k$ festgelegt. | |
| − | + | *Die Anzahl der Zustände ist $2^{m \hspace{0.05cm}\cdot \hspace{0.05cm}k}$.<br> | |
| − | * | ||
| − | * | + | *Von jedem Zustand gehen $2^k$ Pfeile ab.<br> |
| − | + | *Man gelangt auch von jedem Zustand $s_i ∈ \{S_0, \ S_1, \ S_2, \ S_3\}$ zu den gleichen Nachfolgezuständen $s_{i+1}$.<br> | |
| − | *Man gelangt von jedem Zustand $s_i ∈ \{S_0, \ S_1, \ S_2, \ S_3\}$ zu den gleichen Nachfolgezuständen $s_{i+1}$.<br> | ||
| − | *Ein Unterschied besteht hinsichtlich der ausgegebenen Codesequenzen $\underline{x}_i ∈ \{00, 01, 10, 11\}$.<br><br> | + | *Ein Unterschied besteht allein hinsichtlich der ausgegebenen Codesequenzen, wobei in beiden Fällen $\underline{x}_i ∈ \{00, \ 01, \ 10, \ 11\}$ gilt.}}<br><br> |
| − | == Darstellung im Trellisdiagramm | + | == Darstellung im Trellisdiagramm == |
<br> | <br> | ||
| − | Man kommt vom Zustandsübergangsdiagramm zum so genannten <i>Trellisdiagramm</i> (oder kurz: Trellis), indem man zusätzlich eine Zeitkomponente ⇒ Laufvariable $i$ berücksichtigt. Die folgende Grafik stellt | + | Man kommt vom Zustandsübergangsdiagramm zum so genannten <i>Trellisdiagramm</i> (oder kurz: '''Trellis'''), indem man zusätzlich eine Zeitkomponente ⇒ Laufvariable $i$ berücksichtigt. Die folgende Grafik stellt beide Diagramme für unseren „Standard–Codierer” $(n = 2, \ k = 1, \ m = 2)$ gegenüber.<br> |
| − | [[Datei:P ID2635 KC T 3 3 S3 v2.png|Zustandsübergangsdiagramm vs. Trellisdiagramm ( | + | [[Datei:P ID2635 KC T 3 3 S3 v2.png|center|frame|Zustandsübergangsdiagramm vs. Trellisdiagramm $(n = 2, \ k = 1, \ m = 2)$|class=fit]] |
Die untere Darstellung hat Ähnlichkeit mit einem Gartenspalier – etwas Phantasie vorausgesetzt. Die englische Übersetzung hierfür ist „Trellis”. Weiter ist anhand dieser Grafik zu erkennen: | Die untere Darstellung hat Ähnlichkeit mit einem Gartenspalier – etwas Phantasie vorausgesetzt. Die englische Übersetzung hierfür ist „Trellis”. Weiter ist anhand dieser Grafik zu erkennen: | ||
| − | *Da alle Speicherregister mit Nullen vorbelegt sind, startet das Trellis stets vom Zustand $s_1 = S_0$. Zum nächsten Zeitpunkt $(i = 2)$ sind dann nur die beiden Zustände $S_0$ und $S_1$ möglich.<br> | + | *Da alle Speicherregister mit Nullen vorbelegt sind, startet das Trellis stets vom Zustand $s_1 = S_0$. Zum nächsten Zeitpunkt $(i = 2)$ sind dann nur die beiden (Start–)Zustände $S_0$ und $S_1$ möglich.<br> |
| + | |||
| + | *Ab dem Zeitpunkt $i = m + 1 = 3$ hat das Trellis für jeden Übergang von $s_i$ nach $s_{i+1}$ genau das gleiche Aussehen. Jeder Zustand $S_{\mu}$ ist durch einen roten Pfeil $(u_i = 0)$ und einen blauen Pfeil $(u_i = 1)$ mit einem Nachfolgezustand verbunden.<br> | ||
| − | * | + | *Gegenüber einem <i>Codebaum</i>, der mit jedem Zeitschritt $i$ exponentiell anwächst – siehe zum Beispiel Abschnitt [[Digitalsignalübertragung/Viterbi–Empfänger#Fehlergr.C3.B6.C3.9Fen_und_Gesamtfehlergr.C3.B6.C3.9Fen| Fehlergrößen und Gesamtfehlergrößen]] im Buch „Digitalsignalübertragung” – ist hier die Zahl der Knoten (also der möglichen Zustände) auf $2^m$ begrenzt.<br> |
| − | * | + | *Diese erfreuliche Eigenschaft eines jeden Trellisdiagramms nutzt auch der [[Kanalcodierung/Decodierung_von_Faltungscodes| Viterbi–Algorithmus]] zur effizienten Maximum–Likelihood–Decodierung von Faltungscodes.<br><br> |
| − | + | Das folgende Beispiel soll zeigen, dass zwischen der Aneinanderreihung der Codesequenzen $\underline{x}_i$ und den Pfaden durch das Trellisdiagramm eine $1\text{:}1$–Zuordnung besteht. | |
| + | *Auch die Informationssequenz $\underline{u}$ ist aus dem ausgewählten Trellispfad anhand der Farben der einzelnen Zweige ablesbar. | ||
| + | *Ein roter Zweig steht für das Informationsbit $u_i = 0$, ein blauer für $u_i = 1$.<br> | ||
| − | |||
| − | |||
| − | |||
| − | {{Beispiel}} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 2:}$ Im [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister|$\text{Beispiel 1}$]] wurde für unseren Rate–$1/2$–Standardcodierer mit Gedächtnis $m = 2$ sowie die Informationssequenz $\underline{u} = (1, 1, 1, 0, 0, 0, 1, 0, 1, \ \text{...})$ die Codesequenz $\underline{x}$ hergeleitet, die hier für $i ≤ 9$ nochmals angegeben wird.<br> | ||
| − | [[Datei:P ID2636 KC T 3 3 S3b v1.png|Trellisdiagramm einer Beispielssequenz|class=fit]] | + | [[Datei:P ID2636 KC T 3 3 S3b v1.png|center|frame|Trellisdiagramm einer Beispielssequenz|class=fit]] |
Darunter gezeichnet ist das Trellisdiagramm. Man erkennt: | Darunter gezeichnet ist das Trellisdiagramm. Man erkennt: | ||
| − | *Der ausgewählte Pfad durch das Trellis ergibt sich durch die Aneinanderreihung roter und blauer Pfeile, die für die möglichen Informationsbits $u_i | + | *Der ausgewählte Pfad durch das Trellis ergibt sich durch die Aneinanderreihung roter und blauer Pfeile, die für die möglichen Informationsbits $u_i \in \{ 0, \ 1\}$ stehen. Diese Aussage gilt für jeden Rate–$1/n$–Faltungscode. Bei einem Code mit $k > 1$ gäbe es $2^k$ verschiedenfarbige Pfeile.<br> |
| − | *Bei einem Rate–$1/n$–Faltungscode sind die Pfeile mit den Codeworten $\underline{x}_i = (x_i^{(1)}, \ ... \ , \ x_i^{(n)})$ beschriftet, die sich aus dem Informationsbit $u_i$ und den aktuellen Registerzuständen $s_i$ ergeben. Für $n = 2$ gibt es nur vier mögliche Codeworte, nämlich $00, 01, 10$ und $11$.<br> | + | *Bei einem Rate–$1/n$–Faltungscode sind die Pfeile mit den Codeworten $\underline{x}_i = (x_i^{(1)}, \ \text{...} \ , \ x_i^{(n)})$ beschriftet, die sich aus dem Informationsbit $u_i$ und den aktuellen Registerzuständen $s_i$ ergeben. Für $n = 2$ gibt es nur vier mögliche Codeworte, nämlich $00, \ 01, \ 10$ und $11$.<br> |
| − | *In vertikaler Richtung erkennt man aus dem Trellis die | + | *In vertikaler Richtung erkennt man aus dem Trellis die Registerzustände $S_{\mu}$. Bei einem Rate–$k/n$–Faltungscode mit der Gedächtnisordnung $m$ gibt es $2^{k \hspace{0.05cm}\cdot \hspace{0.05cm}m}$ verschiedene Zustände. Im vorliegenden Beispiel $(k = 1, \ m = 2)$ sind dies die Zustände $S_0, \ S_1, \ S_2$ und $S_3$.}}<br> |
| − | == Definition der freien Distanz | + | == Definition der freien Distanz == |
<br> | <br> | ||
| − | + | Eine wichtige Kenngröße der linearen Blockcodes ist die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| minimale Hamming–Distanz]] '''zwischen zwei beliebigen Codeworten''' $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$: | |
| + | |||
| + | ::<math>d_{\rm min}(\mathcal{C}) = | ||
| + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.03cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.03cm}')\hspace{0.05cm}.</math> | ||
| + | |||
| + | *Aufgrund der Linearität gehört zu jedem Blockcode auch das Nullwort $\underline{0}$. Damit ist $d_{\rm min}$ identisch mit dem minimalen [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Gewicht]] $w_{\rm H}(\underline{x})$ eines Codewortes $\underline{x} ≠ \underline{0}$.<br> | ||
| − | + | *Bei Faltungscodes erweist sich allerdings die Beschreibung der Distanzverhältnisse als wesentlich aufwändiger, da ein Faltungscode aus unendlich langen und unendlich vielen Codesequenzen besteht. Deshalb definieren wir hier anstelle der minimalen Hamming–Distanz: | |
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ | ||
| + | *Die <b>freie Distanz</b> $d_{\rm F}$ eines Faltungscodes ist gleich der Anzahl der Bits, in dem sich zwei beliebige Codesequenzen $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$ (mindestens) unterscheiden. | ||
| + | *Anders ausgedrückt: Die freie Distanz ist gleich der ''minimalen'' Hamming–Distanz '''zwischen zwei beliebigen Pfaden''' durch das Trellis.}} | ||
| − | |||
| − | Da Faltungscodes ebenfalls linear sind, kann man auch hier als Bezugssequenz die unendlich lange Nullsequenz heranziehen: $\underline{x} = \underline{0}$. Damit ist die freie Distanz $d_{\rm F}$ gleich dem minimalen Hamming–Gewicht (Anzahl der Einsen) einer Codesequenz $\underline{x} ≠ \underline{0}$.<br> | + | Da Faltungscodes ebenfalls linear sind, kann man auch hier als Bezugssequenz die unendlich lange Nullsequenz heranziehen: $\underline{x}\hspace{0.03cm}' = \underline{0}$. Damit ist die freie Distanz $d_{\rm F}$ gleich dem minimalen Hamming–Gewicht (Anzahl der Einsen) einer Codesequenz $\underline{x} ≠ \underline{0}$.<br> |
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 3:}$ Wir betrachten die Nullsequenz $\underline{0}$ (mit weiß gefüllten Kreisen markiert) sowie zwei andere Codesequenzen $\underline{x}$ sowie $\underline{x}\hspace{0.03cm}'$ (mit gelber bzw. dunkler Hinterlegung) in unserem Standard–Trellis und charakterisieren diese Sequenzen anhand der Zustandsfolgen: | ||
| − | :<math>\underline{0} | + | :<math>\underline{0} =\left ( S_0 \rightarrow S_0 \rightarrow S_0\rightarrow S_0\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 00, 00, 00, 00, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm},</math> |
| − | :<math>\underline{x} | + | :<math>\underline{x} =\left ( S_0 \rightarrow S_1 \rightarrow S_2\rightarrow S_0\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 11, 10, 11, 00, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm},</math> |
| − | :<math>\underline{x} | + | :<math>\underline{x}\hspace{0.03cm}' = \left ( S_0 \rightarrow S_1 \rightarrow S_3\rightarrow S_2\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 11, 01, 01, 11, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm}.</math> |
| − | [[Datei:P ID2638 KC T 3 3 S4b v2.png|Zur Definition der freien Distanz|class=fit]] | + | [[Datei:P ID2638 KC T 3 3 S4b v2.png|center|frame|Zur Definition der freien Distanz|class=fit]] |
Man erkennt aus diesen Darstellungen: | Man erkennt aus diesen Darstellungen: | ||
| − | *Die freie Distanz $d_{\rm F} = 5$ ist gleich dem Hamming–Gewicht $w_{\rm H}(\underline{x})$. Keine andere Sequenz als die gelb hinterlegte unterscheidet sich von $\underline{0}$ um weniger als | + | *Die freie Distanz $d_{\rm F} = 5$ ist gleich dem Hamming–Gewicht $w_{\rm H}(\underline{x})$. Keine andere Sequenz als die gelb hinterlegte unterscheidet sich von $\underline{0}$ um weniger als fünf Bit. Beispielsweise ist $w_{\rm H}(\underline{x}') = 6$.<br> |
| − | *In diesem Beispiel ergibt sich die freie Distanz $d_{\rm F} = 5$ auch als die Hamming–Distanz zwischen den Sequenzen $\underline{x}$ und $\underline{x}'$, die sich genau in fünf Bitpositionen unterscheiden. | + | *In diesem Beispiel ergibt sich die freie Distanz $d_{\rm F} = 5$ auch als die Hamming–Distanz zwischen den Sequenzen $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$, die sich genau in fünf Bitpositionen unterscheiden.}} |
| − | |||
| − | |||
| − | |||
| − | Die freie Distanz $d_{\rm F}$ nimmt mit wachsendem Gedächtnis $m$ zu, vorausgesetzt, man | + | Je größer die freie Distanz $d_{\rm F}$ ist, desto besser ist das „asymptotische Verhalten” des Faltungscoders. |
| + | *Zur genauen Fehlerwahrscheinlichkeitsberechnung benötigt man allerdings ebenso wie bei den linearen Blockcodes die genaue Kenntnis der [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Distanzspektrum_eines_linearen_Codes| Gewichtsfunktion]] (englisch: <i>Weight Enumerator Function</i> ). | ||
| + | *Diese wird für die Faltungscodes im Detail erst im Kapitel [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken|Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken]] angegeben. | ||
| + | <br clear=all> | ||
| + | [[Datei:P ID2639 KC T 3 3 S4c.png|right|frame|Optimale Faltungscodes der Rate $1/2$|class=fit]] | ||
| + | Vorneweg nur einige wenige Bemerkungen: | ||
| + | *Die freie Distanz $d_{\rm F}$ nimmt mit wachsendem Gedächtnis $m$ zu, vorausgesetzt, dass man für die Übertragungsfunktionsmatrix $\mathbf{G}(D)$ geeignete Polynome verwendet. | ||
| + | *In der Tabelle sind für Rate–$1/2$–Faltungscodes die $n = 2$ Polynome zusammen mit dem $d_{\rm F}$–Wert angegeben. | ||
| + | * Von größerer praktischer Bedeutung ist der <i>Industrie–Standardcode</i> mit $m = 6$ ⇒ $64$ Zustände und der freien Distanz $d_{\rm F} = 10$ (in der Tabelle ist dieser rot hinterlegt). | ||
| − | |||
| − | Das folgende Beispiel zeigt, welche Auswirkungen es hat, wenn man ungünstige Polynome zugrundelegt.<br> | + | Das folgende Beispiel zeigt, welche Auswirkungen es hat, wenn man ungünstige Polynome zugrundelegt. |
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 4:}$ Im $\text{Beispiel 3}$ wurde gezeigt, dass unser Standard–Faltungscoder $(n = 2, \ k = 1, \ m = 2)$ die freie Distanz $d_{\rm F} = 5$ aufweist. Dieser basiert auf der Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$, wie aus dem gezeigten Modell (ohne rote Streichung) hervorgeht. | ||
| − | + | [[Datei:P ID2640 KC T 3 3 S4d v3.png|center|frame|Zustandsübergangsdiagramm $\rm C$ für $n = 2, \ k = 1, \ m = 2$|class=fit]] | |
| − | [[ | + | Verwendet man $\mathbf{G}(D) = (1 + D, \ 1 + D^2)$ ⇒ rote Änderung, so ändert sich das Zustandsübergangsdiagramm gegenüber dem [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Darstellung_im_Zustands.C3.BCbergangsdiagramm| Zustandsübergangsdiagramm $\rm A$]] auf den ersten Blick nur wenig. Die Auswirkungen sind aber gravierend: |
| + | *Die freie Distanz ist nun nicht mehr $d_{\rm F} = 5$, sondern nur noch $d_{\rm F} = 3$, wobei die Codesequenz $\underline{x} = (11, \ 01, \ 00, \ 00, \ \text{...})$ mit nur drei Einsen zur Informationssequenz $\underline{u} = \underline{1} = (1, \ 1, \ 1, \ 1, \ \text{...})$ gehört.<br> | ||
| − | + | *Das heißt: Durch nur drei Übertragungsfehler an den Positionen 1, 2, und 4 verfälscht man die Einssequenz $(\underline{1})$ in die Nullsequenz $(\underline{0})$ und produziert so unendlich viele Decodierfehler im Zustand $S_3$.<br> | |
| − | |||
| − | + | *Einen Faltungscodierer mit diesen Eigenschaften bezeichnet man als „katastrophal”. Der Grund für dieses extrem ungünstige Verhalten ist, dass hier die beiden Polynome $1 + D$ und $1 + D^2$ nicht teilerfemd sind.}}<br> | |
| − | |||
| − | *Einen Faltungscodierer mit diesen Eigenschaften bezeichnet man als | ||
== Terminierte Faltungscodes == | == Terminierte Faltungscodes == | ||
<br> | <br> | ||
| − | Bei der theoretischen Beschreibung der Faltungscodes geht man stets von Informationssequenzen $\underline{u}$ und Codesequenzen $\underline{x}$ aus, die per Definition unendlich lang sind. In praktischen Anwendungen | + | Bei der theoretischen Beschreibung der Faltungscodes geht man stets von Informationssequenzen $\underline{u}$ und Codesequenzen $\underline{x}$ aus, die per Definition unendlich lang sind. |
| + | *In praktischen Anwendungen – zum Beispiel [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_GSM|GSM]] und [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_UMTS|UMTS]] – verwendet man dagegen stets eine Informationssequenz endlicher Länge $L$. | ||
| + | *Bei einem Rate–$1/n$–Faltungscode hat dann die Codesequenz mindestens die Länge $n \cdot L$.<br> | ||
| − | |||
| − | Die Grafik | + | [[Datei:P ID2641 KC T 3 3 S5 v2.png|center|frame|Terminierter Faltungscode der Rate $R = 128/260$|class=fit]] |
| + | |||
| + | Die Grafik ohne die graue Hinterlegung rechts zeigt das Trellis unseres Standard–Rate–$1/2$–Faltungscodes bei binärer Eingangsfolge $\underline{u}$ der endlichen Länge $L = 128$. Damit hat die Codefolge $\underline{x}$ die Länge $2 \cdot L = 256$. | ||
| + | |||
| + | Aufgrund des undefinierten Endzustands ist eine vollständige Maximum–Likelihood–Decodierung der gesendeten Folge allerdings nicht möglich. Da man nicht weiß, welcher der Zustände $S_0, \ \text{...} \ , \ S_3$ sich für $i > L$ einstellen würden, wird die Fehlerwahrscheinlichkeit (etwas) größer sein als im Grenzfall $L → ∞$.<br> | ||
Um dies zu verhindern, terminiert man den Faltungscode entsprechend der Hinterlegung in obiger Grafik: | Um dies zu verhindern, terminiert man den Faltungscode entsprechend der Hinterlegung in obiger Grafik: | ||
| − | *Man fügt an die $L = 128$ Informationsbits noch $m = 2$ Nullen an ⇒ $L' = 130$. | + | *Man fügt an die $L = 128$ Informationsbits noch $m = 2$ Nullen an ⇒ $L' = 130$. |
*Damit ergibt sich beispielsweise für den farblich hervorgehobenen Pfad durch das Trellis: | *Damit ergibt sich beispielsweise für den farblich hervorgehobenen Pfad durch das Trellis: | ||
| − | ::<math>\underline{x}' = (11\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 00 \hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm},\hspace{0.05cm} 10\hspace{0.05cm},\hspace{0.05cm}00\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 11 \hspace{0.05cm} ) </math> | + | ::<math>\underline{x}' = (11\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 00 \hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm},\hspace{0.05cm} 10\hspace{0.05cm},\hspace{0.05cm}00\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 11 \hspace{0.05cm} ) \hspace{0.3cm} |
| + | \Rightarrow \hspace{0.3cm}\underline{u}' = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm} ) \hspace{0.05cm}.</math> | ||
| − | + | *Das Trellis endet nun stets (also unabhängig von den Daten) im definierten Endzustand $S_0$ und man erreicht so die bestmögliche Fehlerwahrscheinlichkeit entsprechend Maximum–Likelihood.<br> | |
| − | + | *Die Verbesserung hinsichtlich der Fehlerwahrscheinlichkeit erkauft man sich allerdings auf Kosten einer kleineren Coderate. | |
| − | + | *Bei $L \gg m$ ist dieser Verlust nur gering. Im betrachteten Beispiel ergibt sich anstelle von $R = 0.5$ mit Terminierung die Coderate | |
| − | *Die Verbesserung hinsichtlich der Fehlerwahrscheinlichkeit erkauft man sich allerdings auf Kosten einer kleineren Coderate. | + | :$$R\hspace{0.05cm}' = 0.5 \cdot L/(L + m) \approx 0.492.$$<br> |
== Punktierte Faltungscodes == | == Punktierte Faltungscodes == | ||
<br> | <br> | ||
| − | Wir gehen von einem Faltungscode der Rate $R_0 = 1/n_0$ aus, den wir <i>Muttercode</i> nennen. Streicht man von dessen Codesequenz einige Bits | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ | ||
| + | *Wir gehen von einem Faltungscode der Rate $R_0 = 1/n_0$ aus, den wir <i>Muttercode</i> nennen. | ||
| + | *Streicht man von dessen Codesequenz einige Bits nach einem vorgegebenen Muster, so spricht man von einem <b>punktierten Faltungscode</b> (englisch: <i>Punctured Convolutional Code</i> ) mit der Coderate $R > R_0$.}}<br> | ||
| + | |||
| + | Die Punktierung geschieht mittels der Punktierungsmatrix $\mathbf{P}$ mit folgenden Eigenschaften: | ||
| + | *Die Zeilenzahl ist $n_0$, die Spaltenzahl gleich der Punktierungsperiode $p$, die durch die gewünschte Coderate bestimmt wird.<br> | ||
| + | |||
| + | *Die $n_0 \cdot p$ Matrixelemente $P_{ij}$ sind binär $(0$ oder $1)$. Bei $P_{ij} = 1$ wird das entsprechende Codebit übernommen, bei $P_{ij} = 0$ punktiert.<br> | ||
| − | Die | + | *Die Rate des punktierten Codes ist gleich dem Quotienten aus der Punktierungsperiode $p$ und der Anzahl $N_1$ der Einsen in der $\mathbf{P}$–Matrix.<br> |
| − | |||
| − | |||
| − | + | Man findet günstig punktierte Faltungscodes üblicherweise nur mittels computergestützter Suche. | |
| − | + | Dabei bezeichnet man einen punktierten Faltungscode dann als günstig, wenn er | |
| − | *die gleiche Gedächtnisordnung $m$ aufweist wie der Muttercode (auch die Gesamteinflusslänge ist in beiden Fällen gleich: $\nu = m + 1$ | + | *die gleiche Gedächtnisordnung $m$ aufweist wie der Muttercode $($auch die Gesamteinflusslänge ist in beiden Fällen gleich: $\nu = m + 1)$,<br> |
| − | *eine möglichst große freie Distanz $d_{\rm F}$ besitzt, die natürlich kleiner ist als die des Muttercodes.<br><br> | + | *eine möglichst große freie Distanz $d_{\rm F}$ besitzt, die natürlich kleiner ist als die des Muttercodes.<br><br> |
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 5:}$ Ausgehend von unserem [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister| Rate–1/2–Standardcode]] mit den Parametern $n_0 = 2$ und $m = 2$ erhält man mit der Punktierungsmatrix | ||
| − | :<math>{\boldsymbol{\rm P}} = | + | ::<math>{\boldsymbol{\rm P} } = |
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 1 & 0 \\ | 1 & 1 & 0 \\ | ||
| Zeile 223: | Zeile 253: | ||
\end{pmatrix}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p = 3\hspace{0.05cm}, \hspace{0.2cm}N_1 = 4</math> | \end{pmatrix}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p = 3\hspace{0.05cm}, \hspace{0.2cm}N_1 = 4</math> | ||
| − | einen punktierten Faltungscode der Rate $R = p/N_1 = 3/4$. Wir betrachten hierzu folgende Konstellation: | + | einen punktierten Faltungscode der Rate $R = p/N_1 = 3/4$. Wir betrachten hierzu folgende Konstellation: |
| − | *Informationssequenz: $\hspace{ | + | *Informationssequenz: $\hspace{2.5cm} \underline{u} = (1, 0, 0, 1, 1, 0, \ \text{...}\hspace{0.03cm})$,<br> |
| + | |||
| + | *Codesequenz ohne Punktierung: $\hspace{0.7cm} \underline{x} = (11, 1 \color{grey}{0}, \color{gray}{1}1, 11, 0\color{gray}{1}, \color{gray}{0}1, \ \text{...}\hspace{0.03cm})$,<br> | ||
| − | *Codesequenz | + | *Codesequenz mit Punktierung: $\hspace{0.90cm} \underline{x}\hspace{0.05cm}' = (11, 1\_, \_1, 11, 0\_, \_1, \ \text{...}\hspace{0.03cm})$,<br> |
| − | * | + | *Empfangssequenz ohne Fehler: $\hspace{0.88cm} \underline{y} = (11, 1\_, \_1, 11, 0\_, \_1, \ \text{...}\hspace{0.03cm})$,<br> |
| − | *Empfangssequenz | + | *Modifizierte Empfangssequenz: $\hspace{0.8cm} \underline{y}\hspace{0.05cm}' = (11, 1\rm E, E1, 11, 0E, E1, \ \text{...}\hspace{0.03cm})$.<br> |
| − | |||
| − | Jedes punktierte Bit in der Empfangssequenz $\underline{y}$ (markiert durch einen Unterstrich) wird also durch ein <i>Erasure</i> $\rm E$ ersetzt – siehe [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Erasure_Channel_.E2.80.93_BEC| Binary Erasure Channel]]. Ein solches durch die Punktierung entstandene <i>Erasure</i> wird vom Decoder genauso behandelt wie eine Auslöschung durch den Kanal. | + | Jedes punktierte Bit in der Empfangssequenz $\underline{y}$ (markiert durch einen Unterstrich) wird also durch ein <i>Erasure</i> $\rm E$ ersetzt – siehe [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Erasure_Channel_.E2.80.93_BEC| Binary Erasure Channel]]. Ein solches durch die Punktierung entstandene <i>Erasure</i> wird vom Decoder genauso behandelt wie eine Auslöschung durch den Kanal. |
| − | Natürlich erhöht sich durch die Punktierung die Fehlerwahrscheinlichkeit. Dies kann man bereits daran erkennen, dass die freie Distanz nach der Punktierung auf $d_{\rm F} = 3$ sinkt. Demgegenüber besitzt der Muttercode die freie Distanz $d_{\rm F} = 5$. | + | Natürlich erhöht sich durch die Punktierung die Fehlerwahrscheinlichkeit. Dies kann man bereits daran erkennen, dass die freie Distanz nach der Punktierung auf $d_{\rm F} = 3$ sinkt. Demgegenüber besitzt der Muttercode die freie Distanz $d_{\rm F} = 5$.}}<br> |
| − | Eine Anwendung findet die Punktierung zum Beispiel bei den so genannten RCPC–Codes (<i>Rate Compatible Punctered Convolutional Codes</i>). Näheres hierzu in | + | Eine Anwendung findet die Punktierung zum Beispiel bei den so genannten RCPC–Codes (<i>Rate Compatible Punctered Convolutional Codes</i>). Näheres hierzu in [[Aufgaben:Aufgabe_3.8:_Rate_Compatible_Punctured_Convolutional_Codes| Aufgabe 3.8]].<br> |
| − | == Aufgaben == | + | == Aufgaben zum Kapitel== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.6:_Zustandsübergangsdiagramm|Aufgabe 3.6: Zustandsübergangsdiagramm]] |
| − | [[ | + | [[Aufgaben:Aufgabe_3.6Z:_Übergangsdiagramm_bei_3_Zuständen|Aufgabe 3.6Z: Übergangsdiagramm bei 3 Zuständen]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.7:_Vergleich_zweier_Faltungscodierer|Aufgabe 3.7: Vergleich zweier Faltungscodierer]] |
| − | [[ | + | [[Aufgaben:Aufgabe_3.7Z:_Welcher_Code_ist_katastrophal%3F|Aufgabe 3.7Z: Welcher Code ist katastrophal?]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.8:_Rate_Compatible_Punctured_Convolutional_Codes|Aufgabe 3.8: Rate Compatible Punctured Convolutional Codes]] |
{{Display}} | {{Display}} | ||
Aktuelle Version vom 7. Juni 2019, 14:16 Uhr
Inhaltsverzeichnis
Zustandsdefinition für ein Speicherregister
Ein Faltungscodierer kann auch als Automat mit endlicher Anzahl von Zuständen aufgefasst werden. Die Zustandsanzahl ergibt sich aus der Zahl der Speicherelemente ⇒ Gedächtnis $m$ dabei zu $2^m$.
In diesem Kapitel gehen wir meist vom gezeichneten Faltungscodierer aus, der durch folgende Kenngrößen charakterisiert wird:
- $k = 1, \ n = 2$ ⇒ Coderate $R = 1/2$,
- Gedächtnis $m = 2$ ⇒ Einflusslänge $\nu = 3$,
- Übertragungsfunktionsmatrix in Oktalform $(7, 5)$:
- $$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$
Die Codesequenz zum Zeitpunkt $i$ ⇒ $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ hängt außer vom Informationsbit $u_i$ auch vom Inhalt $(u_{i-1}, \ u_{i-2})$ des Speichers ab.
- Hierfür gibt es $2^m = 4$ Möglichkeiten, nämlich die Zustände $S_0, \ S_1, \ S_2$ und $S_3$.
- Der Registerzustand $S_{\mu}$ sei dabei über den Index definiert:
- \[\mu = u_{i-1} + 2 \cdot u_{i-2}\hspace{0.05cm}, \hspace{0.5cm}{\rm allgemein\hspace{-0.1cm}:}\hspace{0.15cm} \mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} \hspace{0.05cm}.\]
Im Englischen verwendet man für „Zustand” den Begriff „State”. Deshalb ist auch im deutschen Text manchmal vom Registerstatus die Rede.
Um Verwechslungen zu vermeiden, unterscheiden wir im Weiteren durch Groß– bzw. Kleinbuchstaben:
- die möglichen Zustände $S_{\mu}$ mit den Indizes $0 ≤ \mu ≤ 2^m \,-1$,
- die aktuellen Zustände $s_i$ zu den Zeitpunkten $i = 1, \ 2, \ 3, \ \text{...}$
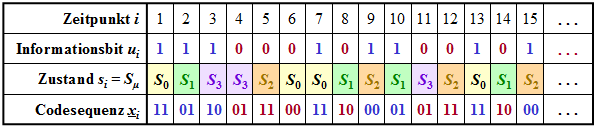
$\text{Beispiel 1:}$ Die Grafik zeigt für den oben skizzierten Faltungscodierer
- die Informationssequenz $\underline{u} = (u_1,u_2, \text{...} \ ) $ ⇒ Informationsbits $u_i$,
- die aktuellen Zustände zu den Zeitpunkten $i$ ⇒ $s_i ∈ \{S_0, \ S_1, \ S_2, \ S_3\}$,
- die 2 Bit–Sequenzen $\underline{x}_i = (x_i^{(1)}, \ x_i^{(2)})$ ⇒ Codierung des Informationsbits $u_i$.
Beispielsweise erkennt man aus dieser Darstellung (die Farben sollen den Übergang zu späteren Grafiken erleichtern):
- Zum Zeitpunkt $i = 5$ gilt $u_{i-1} = u_4 = 0$, $u_{i-2} = u_3 = 1$. Das heißt, der Automat befindet sich im Zustand $s_5 = S_2$. Mit dem Informationsbit $u_i = u_5 = 0$ erhält man die Codesequenz $\underline{x}_5 = (11)$.
- Der Zustand für den Zeitpunkt $i = 6$ ergibt sich aus $u_{i-1} = u_5 = 0$ und $u_{i-2} = u_4 = 0$ zu $s_6 = S_0$. Wegen $u_6 = 0$ wird nun $\underline{x}_6 = (00)$ ausgegeben und der neue Zustand $s_7$ ist wiederum $S_0$.
- Zum Zeitpunkt $i = 12$ wird wegen $u_{12} = 0$ wie zum Zeitpunkt $i = 5$ die Codesequenz $\underline{x}_{12} = (11)$ ausgegeben und man geht vom Zustand $s_{12} = S_2$ in den Zustand $s_{13} = S_0$ über.
- Dagegen wird zum Zeitpunkt $i = 9$ die Codesequenz $\underline{x}_{9} = (00)$ ausgegeben und auf $s_9 = S_2$ folgt $s_{10} = S_1$. Gleiches gilt auch für $i = 15$. In beiden Fällen lautet das aktuelle Informationsbit $u_i = 1$.
$\text{Fazit:}$ Aus diesem Beispiel ist zu erkennen, dass die Codesequenz $\underline{x}_i$ zum Zeitpunkt $i$ allein abhängt
- vom aktuellen Zustand $s_i = S_{\mu} \ \ (0 ≤ \mu ≤ 2^m -1)$, sowie
- vom aktuellen Informationsbit $u_i$.
Ebenso wird der Nachfolgezustand $s_{i+1}$ allein durch $s_i$ und $u_i$ bestimmt.
Diese Eigenschaften werden im so genannten Zustandsübergangsdiagramm auf der nächsten Seite berücksichtigt.
Darstellung im Zustandsübergangsdiagramm
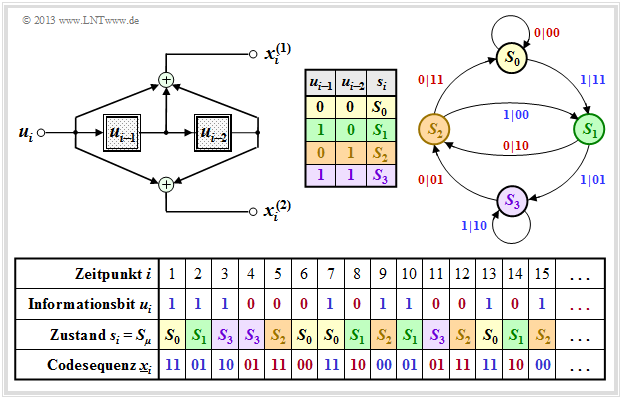
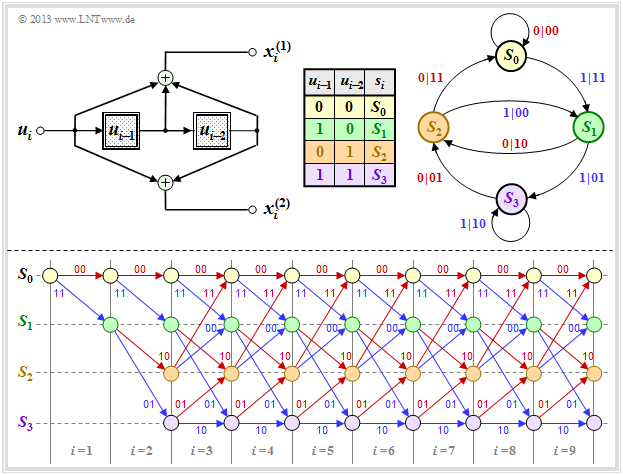
Die Grafik zeigt das Zustandsübergangsdiagramm (englisch: State Transition Diagram ) für unseren „Standard–Codierer”.
- Dieses liefert alle Informationen über den $(n = 2, \ k = 1, \ m = 2)$–Faltungscodierer in kompakter Form.
- Die Farbgebung ist mit der sequenziellen Darstellung auf der vorherigen Seite abgestimmt.
- Der Vollständigkeit halber ist auch die Herleitungstabelle nochmals angegeben.
Die $2^{m+k}$ Übergänge sind mit „$u_i \ | \ \underline{x}_i$” beschriftet. Beispielsweise ist abzulesen:
- Durch das Informationsbit $u_i = 0$ (gekennzeichnet durch eine rote Beschriftung) gelangt man vom Zustand $s_i = S_1$ zum Zustand $s_{i+1} = S_2$ und die beiden Codebits lauten $x_i^{(1)} = 1, \ x_i^{(2)} = 0$.
- Mit dem Informationsbit $u_i = 1$ (blaue Beschriftung) im Zustand $s_i = S_1$ ergeben sich dagegen die Codebits zu $x_i^{(1)} = 0, \ x_i^{(2)} = 1$, und man kommt zum neuen Zustand $s_{i+1} = S_3$.
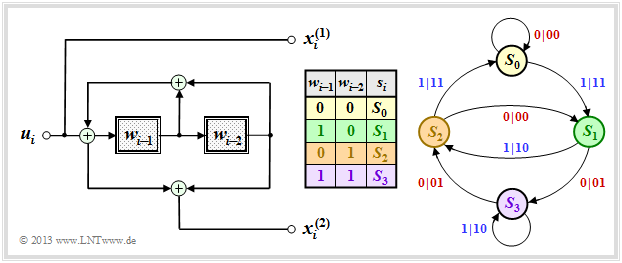
Betrachten wir nun einen weiteren systematischen Code, ebenfalls mit den Kenngrößen $n = 2, \ k = 1, \ m = 2$. Es handelt sich hierbei um die äquivalente systematische Repräsentation des oberen Codierers. Man bezeichnet diesen auch als RSC–Codierer (englisch: Recursive Systematic Convolutional Encoder).
Gegenüber dem oberen Zustandsübergangsdiagramm erkennt man folgende Unterschiede:
- Da die früheren Informationsbits $u_{i-1}$ und $u_{i-2}$ nicht abgespeichert werden, beziehen sich hier die Zustände $s_i = S_{\mu}$ auf die verarbeiteten Größen $w_{i-1}$ und $w_{i-2}$, wobei $w_i = u_i + w_{i-1} + w_{i-2}$ gilt.
- Da dieser Code ebenfalls systematisch ist, gilt wieder $x_i^{(1)} = u_i$. Die Herleitung der zweiten Codebits $x_i^{(2)}$ finden Sie in der Aufgabe 3.5. Es handelt sich um ein rekursives Filter, wie im Abschnitt Filterstruktur bei gebrochen–rationaler Übertragungsfunktion beschrieben.
$\text{Fazit:}$ Der Bildervergleich zeigt, dass sich für beide Codierer ein ähnliches Zustandsübergangsdiagramm ergibt:
- Die Struktur des Zustandsübergangsdiagramms ist allein durch die Parameter $m$ und $k$ festgelegt.
- Die Anzahl der Zustände ist $2^{m \hspace{0.05cm}\cdot \hspace{0.05cm}k}$.
- Von jedem Zustand gehen $2^k$ Pfeile ab.
- Man gelangt auch von jedem Zustand $s_i ∈ \{S_0, \ S_1, \ S_2, \ S_3\}$ zu den gleichen Nachfolgezuständen $s_{i+1}$.
- Ein Unterschied besteht allein hinsichtlich der ausgegebenen Codesequenzen, wobei in beiden Fällen $\underline{x}_i ∈ \{00, \ 01, \ 10, \ 11\}$ gilt.
Darstellung im Trellisdiagramm
Man kommt vom Zustandsübergangsdiagramm zum so genannten Trellisdiagramm (oder kurz: Trellis), indem man zusätzlich eine Zeitkomponente ⇒ Laufvariable $i$ berücksichtigt. Die folgende Grafik stellt beide Diagramme für unseren „Standard–Codierer” $(n = 2, \ k = 1, \ m = 2)$ gegenüber.
Die untere Darstellung hat Ähnlichkeit mit einem Gartenspalier – etwas Phantasie vorausgesetzt. Die englische Übersetzung hierfür ist „Trellis”. Weiter ist anhand dieser Grafik zu erkennen:
- Da alle Speicherregister mit Nullen vorbelegt sind, startet das Trellis stets vom Zustand $s_1 = S_0$. Zum nächsten Zeitpunkt $(i = 2)$ sind dann nur die beiden (Start–)Zustände $S_0$ und $S_1$ möglich.
- Ab dem Zeitpunkt $i = m + 1 = 3$ hat das Trellis für jeden Übergang von $s_i$ nach $s_{i+1}$ genau das gleiche Aussehen. Jeder Zustand $S_{\mu}$ ist durch einen roten Pfeil $(u_i = 0)$ und einen blauen Pfeil $(u_i = 1)$ mit einem Nachfolgezustand verbunden.
- Gegenüber einem Codebaum, der mit jedem Zeitschritt $i$ exponentiell anwächst – siehe zum Beispiel Abschnitt Fehlergrößen und Gesamtfehlergrößen im Buch „Digitalsignalübertragung” – ist hier die Zahl der Knoten (also der möglichen Zustände) auf $2^m$ begrenzt.
- Diese erfreuliche Eigenschaft eines jeden Trellisdiagramms nutzt auch der Viterbi–Algorithmus zur effizienten Maximum–Likelihood–Decodierung von Faltungscodes.
Das folgende Beispiel soll zeigen, dass zwischen der Aneinanderreihung der Codesequenzen $\underline{x}_i$ und den Pfaden durch das Trellisdiagramm eine $1\text{:}1$–Zuordnung besteht.
- Auch die Informationssequenz $\underline{u}$ ist aus dem ausgewählten Trellispfad anhand der Farben der einzelnen Zweige ablesbar.
- Ein roter Zweig steht für das Informationsbit $u_i = 0$, ein blauer für $u_i = 1$.
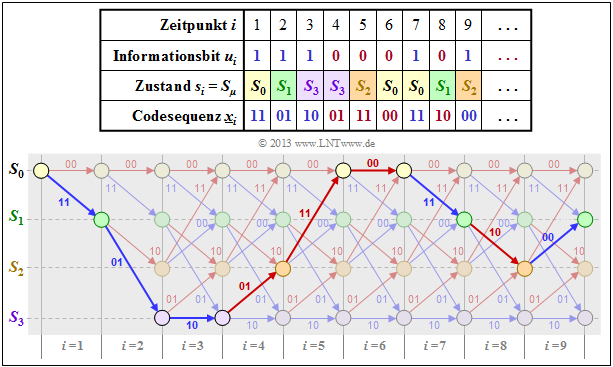
$\text{Beispiel 2:}$ Im $\text{Beispiel 1}$ wurde für unseren Rate–$1/2$–Standardcodierer mit Gedächtnis $m = 2$ sowie die Informationssequenz $\underline{u} = (1, 1, 1, 0, 0, 0, 1, 0, 1, \ \text{...})$ die Codesequenz $\underline{x}$ hergeleitet, die hier für $i ≤ 9$ nochmals angegeben wird.
Darunter gezeichnet ist das Trellisdiagramm. Man erkennt:
- Der ausgewählte Pfad durch das Trellis ergibt sich durch die Aneinanderreihung roter und blauer Pfeile, die für die möglichen Informationsbits $u_i \in \{ 0, \ 1\}$ stehen. Diese Aussage gilt für jeden Rate–$1/n$–Faltungscode. Bei einem Code mit $k > 1$ gäbe es $2^k$ verschiedenfarbige Pfeile.
- Bei einem Rate–$1/n$–Faltungscode sind die Pfeile mit den Codeworten $\underline{x}_i = (x_i^{(1)}, \ \text{...} \ , \ x_i^{(n)})$ beschriftet, die sich aus dem Informationsbit $u_i$ und den aktuellen Registerzuständen $s_i$ ergeben. Für $n = 2$ gibt es nur vier mögliche Codeworte, nämlich $00, \ 01, \ 10$ und $11$.
- In vertikaler Richtung erkennt man aus dem Trellis die Registerzustände $S_{\mu}$. Bei einem Rate–$k/n$–Faltungscode mit der Gedächtnisordnung $m$ gibt es $2^{k \hspace{0.05cm}\cdot \hspace{0.05cm}m}$ verschiedene Zustände. Im vorliegenden Beispiel $(k = 1, \ m = 2)$ sind dies die Zustände $S_0, \ S_1, \ S_2$ und $S_3$.
Definition der freien Distanz
Eine wichtige Kenngröße der linearen Blockcodes ist die minimale Hamming–Distanz zwischen zwei beliebigen Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.03cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.03cm}')\hspace{0.05cm}.\]
- Aufgrund der Linearität gehört zu jedem Blockcode auch das Nullwort $\underline{0}$. Damit ist $d_{\rm min}$ identisch mit dem minimalen Hamming–Gewicht $w_{\rm H}(\underline{x})$ eines Codewortes $\underline{x} ≠ \underline{0}$.
- Bei Faltungscodes erweist sich allerdings die Beschreibung der Distanzverhältnisse als wesentlich aufwändiger, da ein Faltungscode aus unendlich langen und unendlich vielen Codesequenzen besteht. Deshalb definieren wir hier anstelle der minimalen Hamming–Distanz:
$\text{Definition:}$
- Die freie Distanz $d_{\rm F}$ eines Faltungscodes ist gleich der Anzahl der Bits, in dem sich zwei beliebige Codesequenzen $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$ (mindestens) unterscheiden.
- Anders ausgedrückt: Die freie Distanz ist gleich der minimalen Hamming–Distanz zwischen zwei beliebigen Pfaden durch das Trellis.
Da Faltungscodes ebenfalls linear sind, kann man auch hier als Bezugssequenz die unendlich lange Nullsequenz heranziehen: $\underline{x}\hspace{0.03cm}' = \underline{0}$. Damit ist die freie Distanz $d_{\rm F}$ gleich dem minimalen Hamming–Gewicht (Anzahl der Einsen) einer Codesequenz $\underline{x} ≠ \underline{0}$.
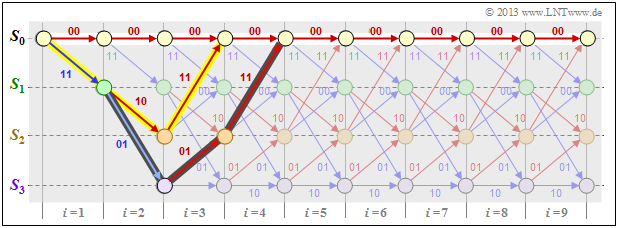
$\text{Beispiel 3:}$ Wir betrachten die Nullsequenz $\underline{0}$ (mit weiß gefüllten Kreisen markiert) sowie zwei andere Codesequenzen $\underline{x}$ sowie $\underline{x}\hspace{0.03cm}'$ (mit gelber bzw. dunkler Hinterlegung) in unserem Standard–Trellis und charakterisieren diese Sequenzen anhand der Zustandsfolgen:
\[\underline{0} =\left ( S_0 \rightarrow S_0 \rightarrow S_0\rightarrow S_0\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 00, 00, 00, 00, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm},\] \[\underline{x} =\left ( S_0 \rightarrow S_1 \rightarrow S_2\rightarrow S_0\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 11, 10, 11, 00, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm},\] \[\underline{x}\hspace{0.03cm}' = \left ( S_0 \rightarrow S_1 \rightarrow S_3\rightarrow S_2\rightarrow S_0\rightarrow \hspace{0.05cm}\text{...} \hspace{0.05cm}\right)= \left ( 11, 01, 01, 11, 00,\hspace{0.05cm} \text{...} \hspace{0.05cm}\right) \hspace{0.05cm}.\]
Man erkennt aus diesen Darstellungen:
- Die freie Distanz $d_{\rm F} = 5$ ist gleich dem Hamming–Gewicht $w_{\rm H}(\underline{x})$. Keine andere Sequenz als die gelb hinterlegte unterscheidet sich von $\underline{0}$ um weniger als fünf Bit. Beispielsweise ist $w_{\rm H}(\underline{x}') = 6$.
- In diesem Beispiel ergibt sich die freie Distanz $d_{\rm F} = 5$ auch als die Hamming–Distanz zwischen den Sequenzen $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$, die sich genau in fünf Bitpositionen unterscheiden.
Je größer die freie Distanz $d_{\rm F}$ ist, desto besser ist das „asymptotische Verhalten” des Faltungscoders.
- Zur genauen Fehlerwahrscheinlichkeitsberechnung benötigt man allerdings ebenso wie bei den linearen Blockcodes die genaue Kenntnis der Gewichtsfunktion (englisch: Weight Enumerator Function ).
- Diese wird für die Faltungscodes im Detail erst im Kapitel Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken angegeben.
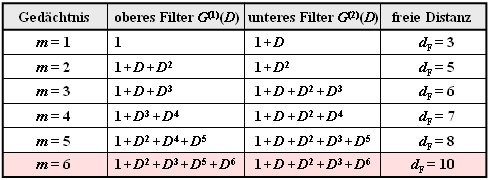
Vorneweg nur einige wenige Bemerkungen:
- Die freie Distanz $d_{\rm F}$ nimmt mit wachsendem Gedächtnis $m$ zu, vorausgesetzt, dass man für die Übertragungsfunktionsmatrix $\mathbf{G}(D)$ geeignete Polynome verwendet.
- In der Tabelle sind für Rate–$1/2$–Faltungscodes die $n = 2$ Polynome zusammen mit dem $d_{\rm F}$–Wert angegeben.
- Von größerer praktischer Bedeutung ist der Industrie–Standardcode mit $m = 6$ ⇒ $64$ Zustände und der freien Distanz $d_{\rm F} = 10$ (in der Tabelle ist dieser rot hinterlegt).
Das folgende Beispiel zeigt, welche Auswirkungen es hat, wenn man ungünstige Polynome zugrundelegt.
$\text{Beispiel 4:}$ Im $\text{Beispiel 3}$ wurde gezeigt, dass unser Standard–Faltungscoder $(n = 2, \ k = 1, \ m = 2)$ die freie Distanz $d_{\rm F} = 5$ aufweist. Dieser basiert auf der Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$, wie aus dem gezeigten Modell (ohne rote Streichung) hervorgeht.
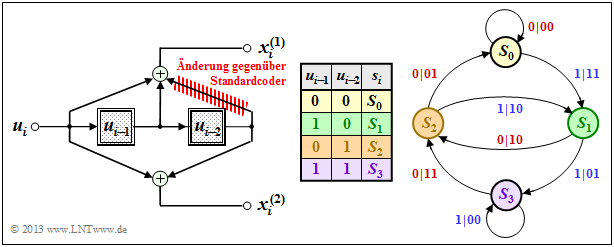
Verwendet man $\mathbf{G}(D) = (1 + D, \ 1 + D^2)$ ⇒ rote Änderung, so ändert sich das Zustandsübergangsdiagramm gegenüber dem Zustandsübergangsdiagramm $\rm A$ auf den ersten Blick nur wenig. Die Auswirkungen sind aber gravierend:
- Die freie Distanz ist nun nicht mehr $d_{\rm F} = 5$, sondern nur noch $d_{\rm F} = 3$, wobei die Codesequenz $\underline{x} = (11, \ 01, \ 00, \ 00, \ \text{...})$ mit nur drei Einsen zur Informationssequenz $\underline{u} = \underline{1} = (1, \ 1, \ 1, \ 1, \ \text{...})$ gehört.
- Das heißt: Durch nur drei Übertragungsfehler an den Positionen 1, 2, und 4 verfälscht man die Einssequenz $(\underline{1})$ in die Nullsequenz $(\underline{0})$ und produziert so unendlich viele Decodierfehler im Zustand $S_3$.
- Einen Faltungscodierer mit diesen Eigenschaften bezeichnet man als „katastrophal”. Der Grund für dieses extrem ungünstige Verhalten ist, dass hier die beiden Polynome $1 + D$ und $1 + D^2$ nicht teilerfemd sind.
Terminierte Faltungscodes
Bei der theoretischen Beschreibung der Faltungscodes geht man stets von Informationssequenzen $\underline{u}$ und Codesequenzen $\underline{x}$ aus, die per Definition unendlich lang sind.
- In praktischen Anwendungen – zum Beispiel GSM und UMTS – verwendet man dagegen stets eine Informationssequenz endlicher Länge $L$.
- Bei einem Rate–$1/n$–Faltungscode hat dann die Codesequenz mindestens die Länge $n \cdot L$.
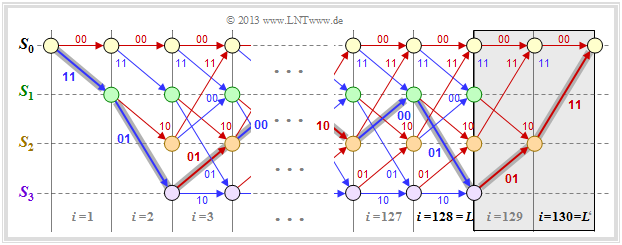
Die Grafik ohne die graue Hinterlegung rechts zeigt das Trellis unseres Standard–Rate–$1/2$–Faltungscodes bei binärer Eingangsfolge $\underline{u}$ der endlichen Länge $L = 128$. Damit hat die Codefolge $\underline{x}$ die Länge $2 \cdot L = 256$.
Aufgrund des undefinierten Endzustands ist eine vollständige Maximum–Likelihood–Decodierung der gesendeten Folge allerdings nicht möglich. Da man nicht weiß, welcher der Zustände $S_0, \ \text{...} \ , \ S_3$ sich für $i > L$ einstellen würden, wird die Fehlerwahrscheinlichkeit (etwas) größer sein als im Grenzfall $L → ∞$.
Um dies zu verhindern, terminiert man den Faltungscode entsprechend der Hinterlegung in obiger Grafik:
- Man fügt an die $L = 128$ Informationsbits noch $m = 2$ Nullen an ⇒ $L' = 130$.
- Damit ergibt sich beispielsweise für den farblich hervorgehobenen Pfad durch das Trellis:
- \[\underline{x}' = (11\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 00 \hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm},\hspace{0.05cm} 10\hspace{0.05cm},\hspace{0.05cm}00\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 01\hspace{0.05cm},\hspace{0.05cm} 11 \hspace{0.05cm} ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{u}' = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.1cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm} ) \hspace{0.05cm}.\]
- Das Trellis endet nun stets (also unabhängig von den Daten) im definierten Endzustand $S_0$ und man erreicht so die bestmögliche Fehlerwahrscheinlichkeit entsprechend Maximum–Likelihood.
- Die Verbesserung hinsichtlich der Fehlerwahrscheinlichkeit erkauft man sich allerdings auf Kosten einer kleineren Coderate.
- Bei $L \gg m$ ist dieser Verlust nur gering. Im betrachteten Beispiel ergibt sich anstelle von $R = 0.5$ mit Terminierung die Coderate
- $$R\hspace{0.05cm}' = 0.5 \cdot L/(L + m) \approx 0.492.$$
Punktierte Faltungscodes
$\text{Definition:}$
- Wir gehen von einem Faltungscode der Rate $R_0 = 1/n_0$ aus, den wir Muttercode nennen.
- Streicht man von dessen Codesequenz einige Bits nach einem vorgegebenen Muster, so spricht man von einem punktierten Faltungscode (englisch: Punctured Convolutional Code ) mit der Coderate $R > R_0$.
Die Punktierung geschieht mittels der Punktierungsmatrix $\mathbf{P}$ mit folgenden Eigenschaften:
- Die Zeilenzahl ist $n_0$, die Spaltenzahl gleich der Punktierungsperiode $p$, die durch die gewünschte Coderate bestimmt wird.
- Die $n_0 \cdot p$ Matrixelemente $P_{ij}$ sind binär $(0$ oder $1)$. Bei $P_{ij} = 1$ wird das entsprechende Codebit übernommen, bei $P_{ij} = 0$ punktiert.
- Die Rate des punktierten Codes ist gleich dem Quotienten aus der Punktierungsperiode $p$ und der Anzahl $N_1$ der Einsen in der $\mathbf{P}$–Matrix.
Man findet günstig punktierte Faltungscodes üblicherweise nur mittels computergestützter Suche.
Dabei bezeichnet man einen punktierten Faltungscode dann als günstig, wenn er
- die gleiche Gedächtnisordnung $m$ aufweist wie der Muttercode $($auch die Gesamteinflusslänge ist in beiden Fällen gleich: $\nu = m + 1)$,
- eine möglichst große freie Distanz $d_{\rm F}$ besitzt, die natürlich kleiner ist als die des Muttercodes.
$\text{Beispiel 5:}$ Ausgehend von unserem Rate–1/2–Standardcode mit den Parametern $n_0 = 2$ und $m = 2$ erhält man mit der Punktierungsmatrix
- \[{\boldsymbol{\rm P} } = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p = 3\hspace{0.05cm}, \hspace{0.2cm}N_1 = 4\]
einen punktierten Faltungscode der Rate $R = p/N_1 = 3/4$. Wir betrachten hierzu folgende Konstellation:
- Informationssequenz: $\hspace{2.5cm} \underline{u} = (1, 0, 0, 1, 1, 0, \ \text{...}\hspace{0.03cm})$,
- Codesequenz ohne Punktierung: $\hspace{0.7cm} \underline{x} = (11, 1 \color{grey}{0}, \color{gray}{1}1, 11, 0\color{gray}{1}, \color{gray}{0}1, \ \text{...}\hspace{0.03cm})$,
- Codesequenz mit Punktierung: $\hspace{0.90cm} \underline{x}\hspace{0.05cm}' = (11, 1\_, \_1, 11, 0\_, \_1, \ \text{...}\hspace{0.03cm})$,
- Empfangssequenz ohne Fehler: $\hspace{0.88cm} \underline{y} = (11, 1\_, \_1, 11, 0\_, \_1, \ \text{...}\hspace{0.03cm})$,
- Modifizierte Empfangssequenz: $\hspace{0.8cm} \underline{y}\hspace{0.05cm}' = (11, 1\rm E, E1, 11, 0E, E1, \ \text{...}\hspace{0.03cm})$.
Jedes punktierte Bit in der Empfangssequenz $\underline{y}$ (markiert durch einen Unterstrich) wird also durch ein Erasure $\rm E$ ersetzt – siehe Binary Erasure Channel. Ein solches durch die Punktierung entstandene Erasure wird vom Decoder genauso behandelt wie eine Auslöschung durch den Kanal.
Natürlich erhöht sich durch die Punktierung die Fehlerwahrscheinlichkeit. Dies kann man bereits daran erkennen, dass die freie Distanz nach der Punktierung auf $d_{\rm F} = 3$ sinkt. Demgegenüber besitzt der Muttercode die freie Distanz $d_{\rm F} = 5$.
Eine Anwendung findet die Punktierung zum Beispiel bei den so genannten RCPC–Codes (Rate Compatible Punctered Convolutional Codes). Näheres hierzu in Aufgabe 3.8.
Aufgaben zum Kapitel
Aufgabe 3.6: Zustandsübergangsdiagramm
Aufgabe 3.6Z: Übergangsdiagramm bei 3 Zuständen
Aufgabe 3.7: Vergleich zweier Faltungscodierer
Aufgabe 3.7Z: Welcher Code ist katastrophal?
Aufgabe 3.8: Rate Compatible Punctured Convolutional Codes