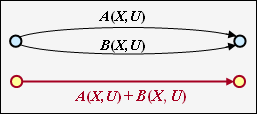Kanalcodierung/Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken: Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== Freie Distanz vs. Minimale Distanz == | == Freie Distanz vs. Minimale Distanz == | ||
<br> | <br> | ||
| − | Eine wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit linearer Blockcodes ist die <i>minimale Distanz</i> zwischen zwei Codeworten: | + | Eine wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit linearer Blockcodes ist die <i>minimale Distanz</i> zwischen zwei Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$: |
::<math>d_{\rm min}(\mathcal{C}) = | ::<math>d_{\rm min}(\mathcal{C}) = | ||
| − | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') |
= | = | ||
\min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}' = \underline{0}$, so dass die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Distanz]] $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.<br> | + | Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}\hspace{0.05cm}' = \underline{0}$, so dass die [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Distanz]] $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.<br> |
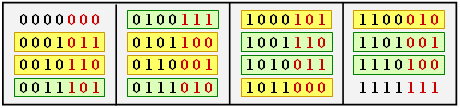
| − | [[Datei:P ID2684 KC T 3 5 S1 neu.png|right|frame| Codewort des $(7, 4, 3)$–Hamming–Codes|class=fit]] | + | [[Datei:P ID2684 KC T 3 5 S1 neu.png|right|frame| Codewort des $(7, 4, 3)$–Hamming–Codes|class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Die Tabelle zeigt die 16 Codeworte des [[Kanalcodierung/Beispiele_binärer_Blockcodes#Hamming.E2.80.93Codes| (7, 4, 3)–Hamming–Codes]].<br> | + | $\text{Beispiel 1:}$ Die Tabelle zeigt die 16 Codeworte des [[Kanalcodierung/Beispiele_binärer_Blockcodes#Hamming.E2.80.93Codes| $(7, 4, 3)$–Hamming–Codes]] <br>$($siehe $\text{Beispiel 7})$.<br> |
| − | *Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$. | + | *Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$. |
| − | *Es gibt sieben Codeworte mit drei Einsen, sieben mit vier Einsen und je eines ohne Einsen bzw. mit sieben Einsen.}} | + | *Es gibt sieben Codeworte mit drei Einsen (gelb hinterlegt), sieben mit vier Einsen (grün hinterlegt) und je eines ohne Einsen bzw. mit sieben Einsen.}} |
<br clear=all> | <br clear=all> | ||
| − | Die <b>freie Distanz</b> $d_{\rm F}$ eines Faltungscodes (<i>Convolution Code</i> ⇒ ${ | + | Die <b>freie Distanz</b> $d_{\rm F}$ eines Faltungscodes (<i>Convolution Code</i> ⇒ $\mathcal{CC}$) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes: |
::<math>d_{\rm F}(\mathcal{CC}) = | ::<math>d_{\rm F}(\mathcal{CC}) = | ||
| − | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') | + | \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') |
= | = | ||
\min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | In der Literatur wird anstelle von $d_{\rm F}$ teilweise auch $d_{∞}$ verwendet. | + | In der Literatur wird anstelle von $d_{\rm F}$ teilweise auch $d_{∞}$ verwendet. |
| − | *Wesentlicher Unterschied zur minimalen Distanz ist, dass bei Faltungscodes nicht Informations– und Codeworte zu betrachten sind, sondern Sequenzen mit der Eigenschaft [[Kanalcodierung/Grundlagen_der_Faltungscodierung#Voraussetzungen_und_Definitionen semi–infinite]].<br> | + | *Wesentlicher Unterschied zur minimalen Distanz ist, dass bei Faltungscodes nicht Informations– und Codeworte zu betrachten sind, sondern Sequenzen mit der Eigenschaft [[Kanalcodierung/Grundlagen_der_Faltungscodierung#Voraussetzungen_und_Definitionen| „semi–infinite”]].<br> |
| − | *Jede Codesequenz $\underline{x}$ beschreibt einen Pfad durch das Trellis. Die freie Distanz ist dabei das kleinstmögliche Hamming–Gewicht eines solchen Pfades (mit Ausnahme des Nullpfades) | + | *Jede Codesequenz $\underline{x}$ beschreibt einen Pfad durch das Trellis. |
| − | + | *Die freie Distanz ist dabei das kleinstmögliche Hamming–Gewicht eines solchen Pfades (mit Ausnahme des Nullpfades).<br> | |
| − | [[Datei:P ID2685 KC T 3 5 S1c v1.png|center|frame| Einige Pfade mit $w(\underline{x}) = d_{\rm F}$|class=fit]] | + | |
| + | Die Grafik zeigt drei der unendlich vielen Pfade mit dem minimalen Hamming–Gewicht $w_{\rm H, \ min}(\underline{x}) = d_{\rm F} = 5$.<br> | ||
| + | |||
| + | [[Datei:P ID2685 KC T 3 5 S1c v1.png|center|frame| Einige Pfade mit $w(\underline{x}) = d_{\rm F} = 5$|class=fit]] | ||
== Pfadgewichtsfunktion== | == Pfadgewichtsfunktion== | ||
<br> | <br> | ||
| − | Für jeden linearen Blockcode lässt sich wegen der endlichen Anzahl an Codeworten $\underline{x}$ in einfacher Weise eine Gewichtsfunktion angeben. Für das | + | Für jeden linearen Blockcode lässt sich wegen der endlichen Anzahl an Codeworten $\underline{x}$ in einfacher Weise eine Gewichtsfunktion angeben. Für das [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Freie_Distanz_vs._Minimale_Distanz|$\text{Beispiel 1}$]] auf der letzten Seite lautet diese: |
::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.</math> | ::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.</math> | ||
| − | Bei einem (nicht terminierten) Faltungscode kann keine solche Gewichtsfunktion angegegeben werden, da es unendlich viele, unendlich lange Codesequenzen $\underline{x}$ gibt, und damit auch unendlich viele Trellispfade. Um dieses Problem in den Griff zu bekommen, gehen wir nun von folgenden Voraussetzungen aus: | + | Bei einem (nicht terminierten) Faltungscode kann keine solche Gewichtsfunktion angegegeben werden, da es unendlich viele, unendlich lange Codesequenzen $\underline{x}$ gibt, und damit auch unendlich viele Trellispfade. Um dieses Problem in den Griff zu bekommen, gehen wir nun von folgenden Voraussetzungen aus: |
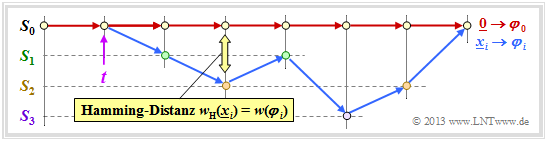
| − | *Als Bezugsgröße für das Trellisdiagramm wählen wir stets den Pfad der Codesequenz $\underline{x} = \underline{0}$ und nennen diesen den <i>Nullpfad</i> $\varphi_0$.<br> | + | *Als Bezugsgröße für das Trellisdiagramm wählen wir stets den Pfad der Codesequenz $\underline{x} = \underline{0}$ und nennen diesen den <i>Nullpfad</i> $\varphi_0$.<br> |
| − | * | + | *Wir betrachten nur noch solche Pfade $\varphi_j ∈ {\it \Phi}$, die alle zu einer vorgegebenen Zeit $t$ vom Nullpfad abweichen und irgendwann wieder zu diesem zurückkehren.<br><br> |
| − | Obwohl nur ein Bruchteil aller | + | Obwohl nur ein Bruchteil aller Pfade zur Menge ${\it \Phi}$ gehören, beinhaltet ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} \}$ noch immer eine unbegrenzte Menge an Pfaden. $\varphi_0$ gehört nicht dazu.<br> |
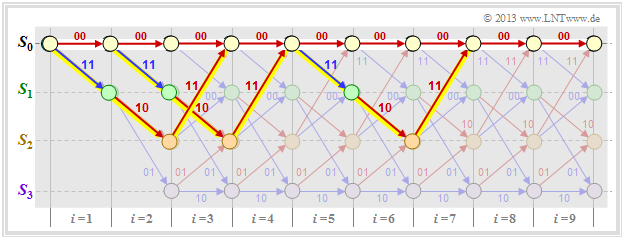
[[Datei:P ID2686 KC T 3 5 S2a v1.png|center|frame|Einige Pfade und ihre Pfadgewichte|class=fit]] | [[Datei:P ID2686 KC T 3 5 S2a v1.png|center|frame|Einige Pfade und ihre Pfadgewichte|class=fit]] | ||
| − | Im obigen Trellis sind einige Pfade $\varphi_j ∈ {\it \Phi}$ eingezeichnet: | + | Im obigen Trellis sind einige Pfade $\varphi_j ∈ {\it \Phi}$ eingezeichnet: |
| − | *Der gelbe Pfad $\varphi_1$ gehört zur Sequenz $\underline{x}_1 = (11, 10, 11)$ mit dem Hamming–Gewicht $w_{\rm H}(\underline{x}_1) = 5$. Damit ist auch das Pfadgewicht $w(\varphi_1) = 5$. Aufgrund der Festlegung des Abzweigzeitpunktes $t$ hat nur noch dieser einzige Pfad $\varphi_1$ die freie Distanz $d_{\rm F} = 5$ zum Nullpfad ⇒ $A_5 = 1$.<br> | + | *Der gelbe Pfad $\varphi_1$ gehört zur Sequenz $\underline{x}_1 = (11, 10, 11)$ mit dem Hamming–Gewicht $w_{\rm H}(\underline{x}_1) = 5$. Damit ist auch das Pfadgewicht $w(\varphi_1) = 5$. Aufgrund der Festlegung des Abzweigzeitpunktes $t$ hat nur noch dieser einzige Pfad $\varphi_1$ die freie Distanz $d_{\rm F} = 5$ zum Nullpfad ⇒ $A_5 = 1$.<br> |
| − | *Für die beiden grünen Pfade mit den korrespondierenden Sequenzen $\underline{x}_2 = (11, 01, 01, 11)$ bzw. $\underline{x}_3 = (11, 10, 00, 10, 11)$ gilt $w(\varphi_2) = w(\varphi_3) = 6$. Kein anderer Pfad weist das Pfadgewicht $6$ auf. Wir berücksichtigen diese Tatsache durch den Koeffizienten $A_6 = 2$.<br> | + | *Für die beiden grünen Pfade mit den korrespondierenden Sequenzen $\underline{x}_2 = (11, 01, 01, 11)$ bzw. $\underline{x}_3 = (11, 10, 00, 10, 11)$ gilt $w(\varphi_2) = w(\varphi_3) = 6$. Kein anderer Pfad weist das Pfadgewicht $6$ auf. Wir berücksichtigen diese Tatsache durch den Koeffizienten $A_6 = 2$.<br> |
| − | *Eingezeichnet ist auch der graue Pfad $\varphi_4$, assoziiert mit der Sequenz $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Auch die Sequenzen $\underline{x}_5 = (11, 01, 01, 00, 10, 11), | + | *Eingezeichnet ist auch der graue Pfad $\varphi_4$, assoziiert mit der Sequenz $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Auch die Sequenzen $\underline{x}_5 = (11, 01, 01, 00, 10, 11)$, $\underline{x}_6 = (11, 10, 00, 01, 01, 11)$ und $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$ haben das Pfadgewicht $7$ ⇒ $A_7 = 4$.<br><br> |
Damit lautet die Pfadgewichtsfunktion: | Damit lautet die Pfadgewichtsfunktion: | ||
| − | :<math>T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} | + | ::<math>T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Die Definition dieser Funktion $T(X)$ lautet:<br> | + | Die Definition dieser Funktion $T(X)$ lautet:<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Für die <b>Pfadgewichtsfunktion</b> (englisch: <i>Path Weight Enumerator Function</i>, PWEF) eines Faltungscodes gilt: | + | $\text{Definition:}$ Für die <b>Pfadgewichtsfunktion</b> (englisch: <i>Path Weight Enumerator Function</i>, PWEF) eines Faltungscodes gilt: |
::<math>T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w | ::<math>T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *${\it \Phi}$ bezeichnet die Menge aller Pfade | + | *${\it \Phi}$ bezeichnet die Menge aller Pfade, die den Nullpfad $\varphi_0$ genau zum festgelegten Zeitpunkt $t$ verlassen und (irgendwann) später zu diesem zurückkehren.<br> |
| − | *Gemäß dem zweiten Gleichungsteil sind die Summanden nach ihren Pfadgewichten $w$ geordnet, wobei $A_w$ die Anzahl der Pfade mit Pfadgewicht $w$ bezeichnet. Die Summe beginnt mit $w = d_{\rm F}$.<br> | + | *Gemäß dem zweiten Gleichungsteil sind die Summanden nach ihren Pfadgewichten $w$ geordnet, wobei $A_w$ die Anzahl der Pfade mit Pfadgewicht $w$ bezeichnet. |
| + | *Die Summe beginnt mit $w = d_{\rm F}$.<br> | ||
| − | *Das Pfadgewicht $w(\varphi_j)$ ist gleich dem Hamming–Gewicht (Anzahl der Einsen) der zum Pfad $\varphi_j$ assoziierten Codesequenz $\underline{x}_j$: | + | *Das Pfadgewicht $w(\varphi_j)$ ist gleich dem Hamming–Gewicht (Anzahl der Einsen) der zum Pfad $\varphi_j$ assoziierten Codesequenz $\underline{x}_j$: |
::<math>w({\varphi_j) = w_{\rm H}(\underline {x} }_j) | ::<math>w({\varphi_j) = w_{\rm H}(\underline {x} }_j) | ||
\hspace{0.05cm}.</math>}}<br> | \hspace{0.05cm}.</math>}}<br> | ||
| − | <i>Hinweis:</i> Die für | + | <i>Hinweis:</i> Die für lineare Blockcodes definierte Gewichtsfunktion $W(X)$ und die Pfadgewichtsfunktion $T(X)$ der Faltungscodes weisen viele Gemeinsamkeiten auf; sie sind jedoch nicht identisch.<br> |
| − | |||
| − | + | Wir betrachten nochmals die Gewichtsfunktion des $(7, 4, 3)$–Hamming–Codes, | |
| − | Wir betrachten nochmals die Gewichtsfunktion des $(7, 4, 3)$–Hamming–Codes | ||
::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},</math> | ::<math>W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},</math> | ||
| − | und die Pfadgewichtsfunktion unseres Standard–Faltungscodierers | + | und die Pfadgewichtsfunktion unseres Standard–Faltungscodierers, |
::<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} </math> | ::<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} </math> | ||
| − | Auffallend ist die „$1$” in der ersten Gleichung, die in der zweiten Gleichung fehlt. Das heißt: Bei den linearen Blockcodes wird das Bezugs–Codewort $\underline{x}_i = \underline{0}$ mitgezählt, wohingegen die Nullcodesequenz $\underline{x}_i = \underline{0}$ bzw. der Nullpfad $\varphi_0$ bei den Faltungscodes ausgeschlossen wird. | + | Auffallend ist die „$1$” in der ersten Gleichung, die in der zweiten Gleichung fehlt. Das heißt: Bei den linearen Blockcodes wird das Bezugs–Codewort $\underline{x}_i = \underline{0}$ mitgezählt, wohingegen die Nullcodesequenz $\underline{x}_i = \underline{0}$ bzw. der Nullpfad $\varphi_0$ bei den Faltungscodes per Definition ausgeschlossen wird. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Persönliche Meinung des Autors:}$ | + | $\text{Persönliche Meinung des Autors:}$ |
| − | Man hätte | + | |
| + | Man hätte $W(X)$ ebenfalls ohne die „$1$” definieren können. Damit wäre unter anderem vermieden worden, dass sich die Bhattacharyya–Schranke für lineare Blockcodes und diejenge für Faltungscodes durch „$-1$” unterscheiden, wie aus den folgenden Gleichungen hervorgeht:<br> | ||
| − | *[[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit# | + | *[[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya| Bhattacharyya–Schranke für lineare Blockcodes]]: ${\rm Pr(Blockfehler)} \le W(X = \beta) -1 |
\hspace{0.05cm},$ | \hspace{0.05cm},$ | ||
| − | + | *[[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Burstfehlerwahrscheinlichkeit_und_Bhattacharyya.E2.80.93Schranke| Bhattacharyya–Schranke für Faltungscodes]]: ${\rm Pr(Burstfehler)} \le T(X = \beta) | |
| − | *[[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Burstfehlerwahrscheinlichkeit_und_Bhattacharyya.E2.80. | ||
\hspace{0.05cm}.$}} | \hspace{0.05cm}.$}} | ||
| − | |||
| − | |||
== Erweiterte Pfadgewichtsfunktion == | == Erweiterte Pfadgewichtsfunktion == | ||
<br> | <br> | ||
| + | Die Pfadgewichtsfunktion $T(X)$ liefert nur Informationen hinsichtlich der Gewichte der Codesequenz $\underline{x}$. | ||
| + | *Mehr Informationen erhält man, wenn zusätzlich auch die Gewichte der Informationssequenz $\underline{u}$ erfasst werden. | ||
| + | *Man benötigt dann zwei Formalparameter $X$ und $U$, wie aus der folgenden Definition hervorgeht.<br> | ||
| + | |||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die <b>erweiterte Pfadgewichtsfunktion</b> (englisch: <i>Enhanced Path Weight Enumerator Function</i>, EPWEF) lautet: | + | $\text{Definition:}$ Die <b>erweiterte Pfadgewichtsfunktion</b> (englisch: <i>Enhanced Path Weight Enumerator Function</i>, EPWEF) lautet: |
::<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} | ::<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Es gelten alle Angaben zur $T(X)$–Definition auf der letzten Seite. Zusätzlich ist zu beachten: | + | Es gelten alle Angaben zur $T(X)$–Definition auf der letzten Seite. Zusätzlich ist zu beachten: |
| − | *Das Pfadeingangsgewicht $u(\varphi_j)$ ist gleich dem Hamming–Gewicht der zum Pfad $\varphi_j$ assoziierten Informationssequenz $\underline{u}_j$. Es wird als Potenz des Formalparameters $U$ ausgedrückt.<br> | + | *Das Pfadeingangsgewicht $u(\varphi_j)$ ist gleich dem Hamming–Gewicht der zum Pfad $\varphi_j$ assoziierten Informationssequenz $\underline{u}_j$. Es wird als Potenz des Formalparameters $U$ ausgedrückt.<br> |
| + | |||
| + | *Der Koeffizient $A_{w, \ u}$ bezeichnet die Anzahl der Pfade $\varphi_j$ mit dem Pfadausgangsgewicht $w(\varphi_j)$ und dem Pfadeingangsgewicht $u(\varphi_j)$. Als Laufvariable für den zweiten Anteil wird $u$ verwendet.<br> | ||
| − | * | + | *Setzt man in der erweiterten Pfadgewichtsfunktion den Formalparameter $U = 1$, so ergibt sich die ursprüngliche Gewichtsfunktion $T(X)$ gemäß der Definition auf der letzten Seite.<br> |
| − | |||
Bei vielen (und allen relevanten) Faltungscodes lässt sich obere Gleichung noch vereinfachen: | Bei vielen (und allen relevanten) Faltungscodes lässt sich obere Gleichung noch vereinfachen: | ||
| − | ::<math>T_{\rm enh}(X, U) =\hspace{0.1cm} \sum_{w = d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} | + | ::<math>T_{\rm enh}(X, U) =\hspace{0.1cm} \sum_{w \ = \ d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} |
\hspace{0.05cm}.</math>}}<br> | \hspace{0.05cm}.</math>}}<br> | ||
| Zeile 140: | Zeile 146: | ||
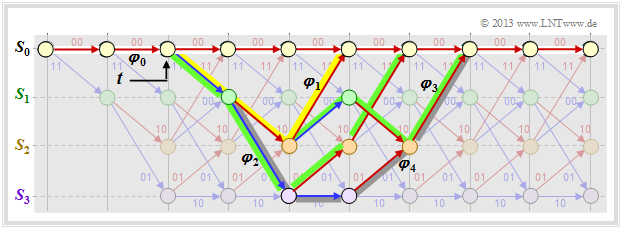
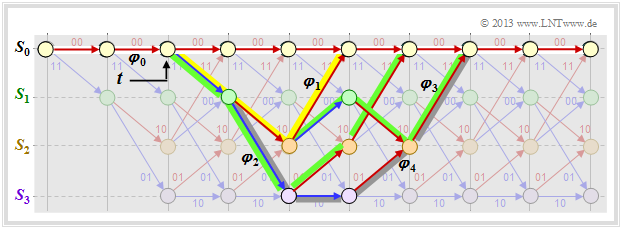
Vergleicht man dieses Ergebnis mit dem unten dargestellten Trellis, so erkennt man: | Vergleicht man dieses Ergebnis mit dem unten dargestellten Trellis, so erkennt man: | ||
| − | *Der gelb hinterlegte Pfad – gekennzeichnet durch $X^5$ – setzt sich aus einem blauen Pfeil $(u_i = 1)$ und zwei roten Pfeilen $(u_i = 0)$ zusammen. Somit wird aus $X^5$ der erweiterte Term $UX^5$.<br> | + | *Der gelb hinterlegte Pfad – gekennzeichnet durch $X^5$ – setzt sich aus einem blauen Pfeil $(u_i = 1)$ und zwei roten Pfeilen $(u_i = 0)$ zusammen. Somit wird aus $X^5$ der erweiterte Term $UX^5$.<br> |
| − | *Die Sequenzen der beiden grünen Pfade sind $\underline{u}_2 = (1, 1, 0, 0)$ ⇒ $\underline{x}_2 = (11, 01, 01, 11)$ sowie $\underline{u}_3 = (1, 0, 1, 0, 0)$ ⇒ $\underline{x}_3 = (11, 10, 00, 10, 11)$. Daraus ergibt sich der zweite Term $2 \cdot U^2X^6$.<br> | + | *Die Sequenzen der beiden grünen Pfade sind $\underline{u}_2 = (1, 1, 0, 0)$ ⇒ $\underline{x}_2 = (11, 01, 01, 11)$ sowie $\underline{u}_3 = (1, 0, 1, 0, 0)$ ⇒ $\underline{x}_3 = (11, 10, 00, 10, 11)$. Daraus ergibt sich der zweite Term $2 \cdot U^2X^6$.<br> |
| + | |||
| + | *Der graue Pfad (und die drei nicht gezeichneten Pfade) ergeben zusammen den Beitrag $4 \cdot U^3X^7$. Jeder dieser Pfade beinhaltet drei blaue Pfeile ⇒ drei Einsen in der zugehörigen Informationssequenz.<br> | ||
| − | |||
[[Datei:P ID2702 KC T 3 5 S2a v1.png|center|frame|Einige Pfade und ihre Pfadgewichte|class=fit]]}} | [[Datei:P ID2702 KC T 3 5 S2a v1.png|center|frame|Einige Pfade und ihre Pfadgewichte|class=fit]]}} | ||
| Zeile 152: | Zeile 159: | ||
== Pfadgewichtsfunktion aus Zustandsübergangsdiagramm == | == Pfadgewichtsfunktion aus Zustandsübergangsdiagramm == | ||
<br> | <br> | ||
| − | Es gibt eine elegante Methode, um die Pfadgewichtsfunktion $T(X)$ und deren Erweiterung direkt aus dem Zustandsübergangsdiagramm zu bestimmen. Dies soll hier und auf den folgenden Seiten am Beispiel unseres [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Zustandsdefinition_f.C3. | + | Es gibt eine elegante Methode, um die Pfadgewichtsfunktion $T(X)$ und deren Erweiterung direkt aus dem Zustandsübergangsdiagramm zu bestimmen. Dies soll hier und auf den folgenden Seiten am Beispiel unseres [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister| Standardcodierers]] demonstriert werden.<br> |
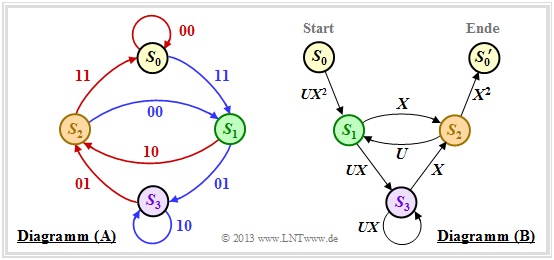
| − | Zunächst muss dazu das Zustandsübergangsdiagramm umgezeichnet werden. Die Grafik zeigt dieses links in der bisherigen Form als Diagramm | + | Zunächst muss dazu das Zustandsübergangsdiagramm umgezeichnet werden. Die Grafik zeigt dieses links in der bisherigen Form als Diagramm $\rm (A)$, während rechts das neue Diagramm $\rm (B)$ angegeben ist.<br> |
[[Datei:P ID2688 KC T 3 5 S3b1 v2.png|center|frame|Zustandsübergangsdiagramm in zwei verschiedenen Varianten|class=fit]] | [[Datei:P ID2688 KC T 3 5 S3b1 v2.png|center|frame|Zustandsübergangsdiagramm in zwei verschiedenen Varianten|class=fit]] | ||
Man erkennt: | Man erkennt: | ||
| − | *Der Zustand $S_0$ wird aufgespalten in den Startzustand $S_0$ und den Endzustand $S_0'$. Damit lassen sich alle Pfade des Trellisdiagramms, die im Zustand $S_0$ beginnen und irgendwann zu diesem zurückkehren, auch im rechten Graphen | + | *Der Zustand $S_0$ wird aufgespalten in den Startzustand $S_0$ und den Endzustand $S_0\hspace{0.01cm}'$. Damit lassen sich alle Pfade des Trellisdiagramms, die im Zustand $S_0$ beginnen und irgendwann zu diesem zurückkehren, auch im rechten Graphen $\rm (B)$ nachvollziehen. Ausgeschlossen sind dagegen direkte Übergänge von $S_0$ nach $S_0\hspace{0.01cm}'$ und damit auch der Nullpfad $($Dauer–$S_0)$.<br> |
| − | *Im Diagramm | + | *Im Diagramm $\rm (A)$ sind die Übergänge anhand der Farben Rot $($für $u_i = 0)$ und Blau $($für $u_i = 1)$ unterscheidbar, und die Codeworte $\underline{x}_i ∈ \{00, 01, 10, 11\}$ sind an den Übergängen vermerkt. Im neuen Diagramm $\rm (B)$ werden $(00)$ durch $X^0 = 1$ und $(11)$ durch $X^2$ ausgedrückt. Die Codeworte $(01)$ und $(10)$ sind nun nicht mehr unterscheidbar, sondern werden einheitlich mit $X$ bezeichnet.<br> |
| − | *Anders formuliert: Das Codewort $\underline{x}_i$ wird nun als $X^w$ dargestellt, wobei $X$ eine dem Ausgang (der Codesequenz) zugeordnete Dummy–Variable ist und $w = w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht des Codewortes $\underline{x}_i$ angibt. Bei einem Rate–$1/2$–Code ist der Exponent $w$ entweder $0, 1$ oder $2$.<br> | + | *Anders formuliert: Das Codewort $\underline{x}_i$ wird nun als $X^w$ dargestellt, wobei $X$ eine dem Ausgang (der Codesequenz) zugeordnete Dummy–Variable ist und $w = w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht des Codewortes $\underline{x}_i$ angibt. Bei einem Rate–$1/2$–Code ist der Exponent $w$ entweder $0, \ 1$ oder $2$.<br> |
| − | *Ebenfalls verzichtet wird im Diagramm | + | *Ebenfalls verzichtet wird im Diagramm $\rm (B)$ auf die Farbcodierung. Das Informationsbit $u_i = 1$ wird nun durch $U^1 = U$ und das Informationsbit $u_i = 0$ durch $U^0 = 1$ gekennzeichnet. Die Dummy–Variable $U$ ist also der Eingangssequenz $\underline{u}$ zugeordnet.<br><br> |
== Regeln zur Manipulation des Zustandsübergangsdiagramms == | == Regeln zur Manipulation des Zustandsübergangsdiagramms == | ||
<br> | <br> | ||
| − | Ziel unserer Berechnungen wird es sein, den (beliebig komplizierten) Weg von $S_0$ nach $S_0'$ durch die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \ U)$ zu charakterisieren. Dazu benötigen wir Regeln, um den Graphen schrittweise vereinfachen zu können.<br><br> | + | Ziel unserer Berechnungen wird es sein, den (beliebig komplizierten) Weg von $S_0$ nach $S_0\hspace{0.01cm}'$ durch die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \ U)$ zu charakterisieren. Dazu benötigen wir Regeln, um den Graphen schrittweise vereinfachen zu können.<br><br> |
[[Datei:P ID2689 KC T 3 5 S3b1.png|right|frame|Erfassung serieller Übergänge]] | [[Datei:P ID2689 KC T 3 5 S3b1.png|right|frame|Erfassung serieller Übergänge]] | ||
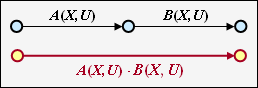
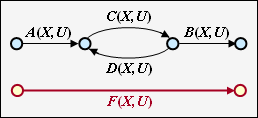
| − | + | '''Serielle Übergänge''' | |
| − | Zwei serielle Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – können durch eine einzige Verbindung mit dem Produkt dieser Bewertungen ersetzt werden.<br> | + | Zwei serielle Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – können durch eine einzige Verbindung mit dem Produkt dieser Bewertungen ersetzt werden.<br> |
<br clear=all> | <br clear=all> | ||
[[Datei:P ID2690 KC T 3 5 S3b2.png|right|frame|Erfassung paralleler Übergänge]] | [[Datei:P ID2690 KC T 3 5 S3b2.png|right|frame|Erfassung paralleler Übergänge]] | ||
| − | + | '''Parallele Übergänge''' | |
| − | Zwei parallele Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – werden durch die Summe ihrer Bewertungsfunktionen zusammengefasst.<br> | + | |
| + | Zwei parallele Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – werden durch die Summe ihrer Bewertungsfunktionen zusammengefasst.<br> | ||
<br clear=all> | <br clear=all> | ||
[[Datei:P ID2691 KC T 3 5 S3b3.png|right|frame|Reduzierung eines Rings]] | [[Datei:P ID2691 KC T 3 5 S3b3.png|right|frame|Reduzierung eines Rings]] | ||
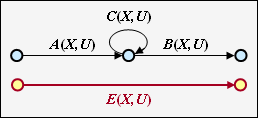
| − | + | '''Ring''' | |
| + | |||
Die nebenstehende Konstellation kann durch eine einzige Verbindung ersetzt werden, wobei für die Ersetzung gilt: | Die nebenstehende Konstellation kann durch eine einzige Verbindung ersetzt werden, wobei für die Ersetzung gilt: | ||
::<math>E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} | ::<math>E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} | ||
| Zeile 187: | Zeile 196: | ||
<br clear=all> | <br clear=all> | ||
[[Datei:P ID2692 KC T 3 5 S3b4.png|right|frame|Reduzierung einer Rückkopplung ]] | [[Datei:P ID2692 KC T 3 5 S3b4.png|right|frame|Reduzierung einer Rückkopplung ]] | ||
| − | + | '''Rückkopplung''' | |
| + | |||
Durch die Rückkopplung können sich hier zwei Zustände beliebig oft abwechseln. Für diese Konstellation gilt: | Durch die Rückkopplung können sich hier zwei Zustände beliebig oft abwechseln. Für diese Konstellation gilt: | ||
::<math>F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} | ::<math>F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Die hier angegebenen Gleichungen für Ring und Rückkopplung sind in [[Aufgabe 3.12Z]] zu beweisen. | + | Die hier angegebenen Gleichungen für Ring und Rückkopplung sind in der [[Aufgaben:Aufgabe_3.12Z:_Ring_und_Rückkopplung|Aufgabe 3.12Z]] zu beweisen. |
<br clear=all> | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 3:}$ | $\text{Beispiel 3:}$ | ||
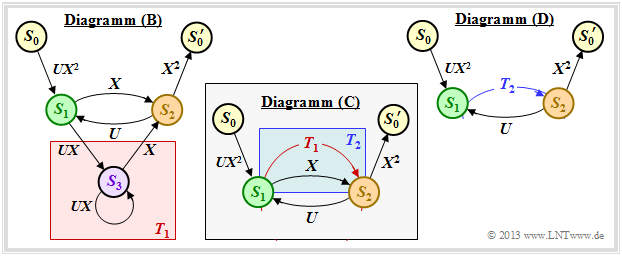
| − | Die oben genannten Regeln sollen nun auf unser Standardbeispiel angewendet werden. In der Grafik sehen Sie links das modifizierte | + | Die oben genannten Regeln sollen nun auf unser Standardbeispiel angewendet werden. In der Grafik sehen Sie links das modifizierte Diagramm $\rm (B)$. |
[[Datei:P ID2695 KC T 3 5 S3a v2.png|center|frame|Zur Reduktion der Zustandsübergänge|class=fit]] | [[Datei:P ID2695 KC T 3 5 S3a v2.png|center|frame|Zur Reduktion der Zustandsübergänge|class=fit]] | ||
| − | *Zunächst ersetzen wir den rot hinterlegten Umweg von $S_1$ nach $S_2$ über $S_3$ im Diagramm | + | *Zunächst ersetzen wir den rot hinterlegten Umweg von $S_1$ nach $S_2$ über $S_3$ im Diagramm $\rm (B)$ durch die im Diagramm $\rm (C)$ eingezeichnete rote Verbindung $T_1(X, \hspace{0.05cm} U)$. Es handelt sich nach der oberen Klassifizierung um einen „Ring” mit den Beschriftungen $A = C = U \cdot X$ und $B = X$, und wir erhalten für die <i>erste Reduktionsfunktion</i>: |
::<math>T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} | ::<math>T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Nun fassen wir die parallelen Verbindungen entsprechend der blauen Hinterlegung im Diagramm | + | *Nun fassen wir die parallelen Verbindungen entsprechend der blauen Hinterlegung im Diagramm $\rm (C)$ zusammen und ersetzen diese durch die blaue Verbindung im Diagramm $\rm (D)$. Die <i>zweite Reduktionsfunktion</i> lautet somit: |
::<math>T_2(X, \hspace{0.05cm}U) = T_1(X, \hspace{0.05cm}U) + X = \frac{U X^2 + X \cdot (1-UX)}{1- U X} = \frac{X}{1- U X} | ::<math>T_2(X, \hspace{0.05cm}U) = T_1(X, \hspace{0.05cm}U) + X = \frac{U X^2 + X \cdot (1-UX)}{1- U X} = \frac{X}{1- U X} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Der gesamte Graph | + | *Der gesamte Graph $\rm (D)$ kann dann durch eine einzige Verbindung von $S_0$ nach $S_0\hspace{0.01cm}'$ ersetzt werden. Nach der Rückkopplungsregel erhält man für die <i>erweiterte Pfadgewichtsfunktion</i>: |
::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} | ::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $ lässt sich hierfür auch schreiben: | + | *Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $ lässt sich hierfür auch schreiben: |
| − | ::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \ | + | ::<math>T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \big [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + \text{...} \hspace{0.05cm} \big ] |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *Setzt man die formale Input–Variable $U = 1$, so erhält man die „einfache” Pfadgewichtsfunktion, die allein Aussagen über die Gewichtsverteilung der Ausgangssequenz $\underline{x}$ erlaubt: | + | *Setzt man die formale Input–Variable $U = 1$, so erhält man die „einfache” Pfadgewichtsfunktion, die allein Aussagen über die Gewichtsverteilung der Ausgangssequenz $\underline{x}$ erlaubt: |
| − | ::<math>T(X) = X^5 \cdot \ | + | ::<math>T(X) = X^5 \cdot \big [ 1 + 2 X + 4 X^2 + 8 X^3 +\text{...}\hspace{0.05cm} \big ] |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | :Das gleiche Ergebnis haben wir bereits aus dem Trellisdiagramm auf [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken# | + | :Das gleiche Ergebnis haben wir bereits aus dem Trellisdiagramm auf der Seite [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Pfadgewichtsfunktion| Pfadgewichtsfunktion]] abgelesen. Dort gab es einen grauen Pfad mit Gewicht $5$, zwei gelbe Pfade mit Gewicht $6$ und vier grüne Pfade mit Gewicht $7$.}}<br> |
| − | == Burstfehlerwahrscheinlichkeit | + | == Blockfehlerwahrscheinlichkeit vs. Burstfehlerwahrscheinlichkeit == |
<br> | <br> | ||
| − | Das | + | [[Datei:P ID2705 KC T 3 5 S5 v1.png|right|frame|Einfaches Übertragungsmodell inklusive Codierung/Decodierung|class=fit]] |
| + | Das einfache Modell gemäß der Skizze gilt sowohl für lineare Blockcodes als auch für Faltungscodes.<br> | ||
| + | |||
| + | |||
| + | '''Blockcodes''' | ||
| + | |||
| + | Bei den Blockcodes bezeichnen $\underline{u} = (u_1, \ \text{...} \hspace{0.05cm}, \ u_i, \ \text{...} \hspace{0.05cm}, \ u_k)$ und $\underline{v} = (v_1, \ \text{...} \hspace{0.05cm}, v_i, \ \text{...} \hspace{0.05cm} \ , \ v_k)$ die Informationsblöcke am Eingang und Ausgang des Systems. | ||
| + | |||
| + | Damit sind folgende Beschreibungsgrößen angebbar: | ||
| + | *die <i>Blockfehlerwahrscheinlichkeit</i> ${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} ≠ \underline{u}),$ | ||
| − | + | *die <i>Bitfehlerwahrscheinlichkeit</i> ${\rm Pr(Bitfehler)} = {\rm Pr}(v_i ≠ u_i).$<br><br> | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Bitte beachten Sie:}$ Bei realen Übertragungssystemen gilt aufgrund des thermischen Rauschens stets: | |
| + | :$${\rm Pr(Bitfehler)} > 0\hspace{0.05cm},\hspace{1.0cm}{\rm Pr(Blockfehler)} > {\rm Pr(Bitfehler)} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | *die | + | Hierfür ein einfacher Erklärungsversuch: Entscheidet der Decoder in jedem Block der Länge $k$ genau ein Bit falsch, |
| + | *so beträgt auch die mittlere Bitfehlerwahrscheinlichkeit ${\rm Pr(Bitfehler)}= 1/k$, | ||
| + | *während für die Blockfehlerwahrscheinlichkeit ${\rm Pr(Blockfehler)}\equiv 1$ gilt.}}<br> | ||
| − | |||
| − | + | '''Faltungscodes''' | |
| − | |||
| − | + | Bei Faltungscodes ist die Blockfehlerwahrscheinlichkeit nicht angebbar, da hier $\underline{u} = (u_1, \ u_2, \ \text{...} \hspace{0.05cm})$ und $\underline{\upsilon} = (v_1, \ v_2, \ \text{...} \hspace{0.05cm})$ Sequenzen darstellen. | |
| − | + | Selbst der kleinstmögliche Codeparameter $k = 1$ führt hier zur Sequenzlänge $k \hspace{0.05cm}' → ∞$, und die Blockfehlerwahrscheinlichkeit ergäbe sich stets zu ${\rm Pr(Blockfehler)}\equiv 1$, selbst wenn die Bitfehlerwahrscheinlichkeit extrem klein (aber ungleich Null) ist.<br> | |
| − | [[Datei:P ID2706 KC T 3 5 S5b v1.png|center|frame|Nullpfad ${\it \ | + | [[Datei:P ID2706 KC T 3 5 S5b v1.png|center|frame|Nullpfad ${\it \varphi}_0$ und Abweichungspfade ${\it \varphi}_i$|class=fit]] |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Für die <b>Burstfehlerwahrscheinlichkeit</b> eines Faltungscodes gilt: | ||
| − | :<math>{\rm Pr(Burstfehler)} = {\rm Pr}\big \{{\rm Decoder\hspace{0.15cm} verl\ddot{a}sst\hspace{0.15cm} zur\hspace{0.15cm} Zeit}\hspace{0.15cm}t \hspace{0.15cm}{\rm den \hspace{0.15cm}korrekten \hspace{0.15cm}Pfad}\big \} | + | ::<math>{\rm Pr(Burstfehler)} = {\rm Pr}\big \{ {\rm Decoder\hspace{0.15cm} verl\ddot{a}sst\hspace{0.15cm} zur\hspace{0.15cm} Zeit}\hspace{0.15cm}t \hspace{0.15cm}{\rm den \hspace{0.15cm}korrekten \hspace{0.15cm}Pfad}\big \} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Um für die folgende Herleitung die Schreibweise zu vereinfachen, gehen wir stets von der Nullsequenz $(\underline{0})$ aus, die im gezeichneten Trellis als Nullpfad $\varphi_0$ rot dargestellt ist. Alle anderen | + | *Um für die folgende Herleitung die Schreibweise zu vereinfachen, gehen wir stets von der Nullsequenz $(\underline{0})$ aus, die im gezeichneten Trellis als Nullpfad $\varphi_0$ rot dargestellt ist. |
| + | *Alle anderen Pfade $\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} $ (und noch viele mehr) verlassen $\varphi_0$ zur Zeit $t$. Sie alle gehören zur Pfadmenge ${\it \Phi}$ ⇒ „Viterbi–Decoder verlässt den korrekten Pfad zur Zeit $t$”. Diese Wahrscheinlichkeit wird auf der nächsten Seite berechnet.}}<br> | ||
| − | == Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke | + | == Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke == |
<br> | <br> | ||
| − | Wir gehen wie | + | Wir gehen wie im früheren Kapitel [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit|Schranken für die Blockfehlerwahrscheinlichkeit]] von der paarweisen Fehlerwahrscheinlichkeit ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ aus, dass der Decoder anstelle des Pfades $\varphi_0$ den Pfad $\varphi_i$ auswählen <b>könnte</b>. Alle betrachteten Pfade $\varphi_i$ verlassen den Nullpfad $\varphi_0$ zum Zeitpunkt $t$; sie gehören somit alle zur Pfadmenge ${\it \Phi}$.<br> |
| − | [[Datei:P ID2707 KC T 3 5 S5c v1.png|center|frame|Zur Berechnung der Burstfehlerwahrscheinlichkeit|class=fit]] | + | [[Datei:P ID2707 KC T 3 5 S5c v1.png|center|frame|Zur Berechnung der Burstfehlerwahrscheinlichkeit|class=fit]] |
| − | Die gesuchte <b>Burstfehlerwahrscheinlichkeit</b> ist gleich der folgenden Vereinigungsmenge: | + | Die gesuchte <b>Burstfehlerwahrscheinlichkeit</b> ist gleich der folgenden Vereinigungsmenge: |
| − | :<math>{\rm Pr(Burstfehler)}= {\rm Pr}\left ([\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}]\hspace{0.05cm}\cup\hspace{0.05cm} ...\hspace{0.05cm} \right )= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}] \right )\hspace{0.05cm}.</math> | + | ::<math>{\rm Pr(Burstfehler)}= {\rm Pr}\left (\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}\big] \hspace{0.05cm}\cup\hspace{0.05cm}\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}\big]\hspace{0.05cm}\cup\hspace{0.05cm} \text{... }\hspace{0.05cm} \right )= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} \big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big] \right )\hspace{0.05cm}.</math> |
| − | Eine obere Schranke hierfür bietet die so genannte [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit| Union–Bound]] | + | Eine obere Schranke hierfür bietet die so genannte [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit| Union–Bound]]: |
| − | :<math>{\rm Pr(Burstfehler)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} | + | ::<math>{\rm Pr(Burstfehler)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} |
| − | {\rm Pr}\ | + | {\rm Pr}\big [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big ] = {\rm Pr(Union \hspace{0.15cm}Bound)} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Die paarweise Fehlerwahrscheinlichkeit kann mit der [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya_.281.29| Bhattacharyya–Schranke]] abgeschätzt werden: | + | Die paarweise Fehlerwahrscheinlichkeit kann mit der [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya_.281.29| Bhattacharyya–Schranke]] abgeschätzt werden: |
| − | :<math>{\rm Pr}\ | + | ::<math>{\rm Pr}\big [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\big ] |
\le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] | {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] | ||
| Zeile 280: | Zeile 303: | ||
\hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.</math> | \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.</math> | ||
| − | $w_{\rm H}(\underline{x}_i)$ | + | Hierbei bezeichnet |
| + | |||
| + | *$w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht der möglichen Codesequenz $\underline{x}_i,$ | ||
| + | *$\ w(\varphi_i)$ das Pfadgewicht des entsprechenden Pfades $\varphi_i ∈ {\it \Phi}$, und | ||
| + | *$\beta$ den so genannten [[Kanalcodierung/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya| Bhattacharyya–Kanalparameter]].<br> | ||
| + | |||
| − | Durch Summation über alle Pfade und einen Vergleich mit der (einfachen) [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken# | + | Durch Summation über alle Pfade und einen Vergleich mit der (einfachen) [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Pfadgewichtsfunktion| Pfadgewichtsfunktion]] $T(X)$ erhalten wir das Ergebnis: |
| − | :<math>{\rm Pr(Burstfehler)} \le T(X = \beta),\hspace{0.5cm}{\rm mit}\hspace{0.5cm} | + | ::<math>{\rm Pr(Burstfehler)} \le T(X = \beta),\hspace{0.5cm}{\rm mit}\hspace{0.5cm} |
T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} | T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} | ||
| − | \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.</math | + | \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.</math> |
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 4:}$ Für unseren Standardcodierer ⇒ $R = 1/2, \ \ m = 2, \ \ \mathbf{G}(D) = (1 + D + D^2, \ 1 + D)$ haben wir folgende [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Pfadgewichtsfunktion| Pfadgewichtsfunktion]] erhalten: | ||
| − | :<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + ... \hspace{0.1cm} | + | ::<math>T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + \ \text{...} \hspace{0.1cm} |
| − | = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ ... \hspace{0.1cm}) | + | = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ \ \text{...} \hspace{0.1cm}) |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ ... \ $ kann hierfür auch geschrieben werden: | + | Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \hspace{0.15cm} $ kann hierfür auch geschrieben werden: |
| − | :<math>T(X) = \frac{X^5}{1-2 \cdot X} | + | ::<math>T(X) = \frac{X^5}{1-2 \cdot X} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Das BSC–Modell liefert mit der Verfälschungswahrscheinlichkeit $\ | + | Das BSC–Modell liefert mit der Verfälschungswahrscheinlichkeit $\varepsilon$ folgende Bhattacharyya–Schranke: |
| − | :<math>{\rm Pr(Burstfehler)} \le T(X = \beta) = T( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}) | + | ::<math>{\rm Pr(Burstfehler)} \le T(X = \beta) = T\big ( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)} \big ) |
= \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.</math> | = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.</math> | ||
| − | In Aufgabe | + | In der [[Aufgaben:Aufgabe_3.14:_Fehlerwahrscheinlichkeitsschranken|Aufgabe 3.14]] soll diese Gleichung numerisch ausgewertet werden.}}<br> |
| − | == Bitfehlerwahrscheinlichkeit und Viterbi–Schranke | + | == Bitfehlerwahrscheinlichkeit und Viterbi–Schranke == |
<br> | <br> | ||
| − | Abschließend wird eine obere Schranke für die Bitfehlerwahrscheinlichkeit angegeben. | + | Abschließend wird eine obere Schranke für die Bitfehlerwahrscheinlichkeit angegeben. Gemäß der Grafik gehen wir wie in [Liv10]<ref name='Liv10'>Liva, G.: ''Channel Coding''. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.</ref> von folgenden Gegebenheiten aus:<br> |
| + | |||
| + | *Gesendet wurde die Nullsequenz $\underline{x} = \underline{0}$ ⇒ Pfad $\varphi_0$.<br> | ||
| − | + | *Die Dauer einer Pfadabweichung (englisch: <i>Error Burst Duration</i> ) wird mit $L$ bezeichnet.<br> | |
| − | * | + | *Den Abstand zweier Bursts (englisch: <i>Inter–Burst Time</i> ) nennen wir $N$.<br> |
| − | * | + | *Das Hamming–Gewicht des Fehlerbündels sei $H$.<br> |
| − | |||
| − | + | [[Datei:P ID2715 KC T 3 5 S6a v1.png|center|frame|Zur Definition der Beschreibungsgrößen $L$, $N$ und $H$|class=fit]] | |
| − | Für einen Rate–$1/n$–Faltungscode ⇒ $k = 1$, also einem Informationsbit pro Takt, lässt sich aus den Erwartungswerten $E[L], \ E[N]$ und $E[H]$ der oben definierten Zufallsgrößen eine obere Schranke für die Bitfehlerwahrscheinlichkeit angeben: | + | Für einen Rate–$1/n$–Faltungscode ⇒ $k = 1$, also einem Informationsbit pro Takt, lässt sich aus den Erwartungswerten ${\rm E}\big[L \big]$, ${\rm E}\big[N \big]$ und ${\rm E}\big[H\big]$ der oben definierten Zufallsgrößen eine obere Schranke für die Bitfehlerwahrscheinlichkeit angeben: |
| − | :<math>{\rm Pr(Bitfehler)} = \frac{{\rm E}[H]}{{\rm E}[L] + {\rm E}[N]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}[H]}{{\rm E}[N]} | + | ::<math>{\rm Pr(Bitfehler)} = \frac{{\rm E}\big[H\big]}{{\rm E}[L] + {\rm E}\big[N\big]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}\big[H\big]}{{\rm E}\big[N\big]} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Hierbei ist vorausgesetzt, dass die (mittlere) Dauer eines Fehlerbündels in der Praxis sehr viel kleiner ist als der zu erwartende Abstand zweier Bündel | + | Hierbei ist vorausgesetzt, dass |
| + | *die (mittlere) Dauer eines Fehlerbündels in der Praxis sehr viel kleiner ist als der zu erwartende Abstand zweier Bündel, | ||
| + | *die (mittlere) <i>Inter–Burst Time</i> $E\big[N\big]$ gleich dem Kehrwert der Burstfehlerwahrscheinlichkeit ist, | ||
| + | *der Erwartungswert im Zähler wie folgt abgeschätzt wird: | ||
| − | :<math>{\rm E}[H] \le \frac{1}{\rm Pr(Burstfehler)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} | + | ::<math>{\rm E}\big[H \big] \le \frac{1}{\rm Pr(Burstfehler)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} |
\hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} | \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Bei der Herleitung dieser Schranke | + | Bei der Herleitung dieser Schranke werden die <i>paarweise Fehlerwahrscheinlichkeit</i> ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ sowie die <i>Bhattacharyya–Abschätzung</i> verwendet. Damit erhält man mit |
| − | *dem Pfadeingangsgewicht $u(\varphi_i),$ | + | *dem Pfadeingangsgewicht $u(\varphi_i),$ |
| + | *dem Pfadausgangsgewicht $w(\varphi_i),$ und | ||
| + | *dem Bhattacharyya–Parameter $\beta$ | ||
| − | |||
| − | + | die folgende Abschätzung für die Bitfehlerwahrscheinlichkeit und bezeichnet diese als die <b>Viterbi–Schranke</b>: | |
| − | + | ::<math>{\rm Pr(Bitfehler)}\le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} | |
| − | + | \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} | |
| − | :<math>{\rm Pr(Bitfehler) | ||
| − | \hspace{0. | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | Dieses Zwischenergebnis lässt sich auch in anderer Form darstellen. Wir erinnern uns an die [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken#Erweiterte_Pfadgewichtsfunktion| erweiterte Pfadgewichtsfunktion]] | ||
| − | + | ::<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | :<math>T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Leitet man diese Funktion nach der Dummy–Eingangsvariablen $U$ ab, so erhält man | + | Leitet man diese Funktion nach der Dummy–Eingangsvariablen $U$ ab, so erhält man |
| − | :<math>\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} | + | ::<math>\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | Setzen wir schließlich noch für die Dummy–Eingangsvariable $U = 1$, so erkennen wir den Zusammenhang zum obigen Ergebnis: | |
| − | :<math>\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.</math> | + | ::<math>\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.</math> |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Fazit:}$ Die <b>Bitfehlerwahrscheinlichkeit</b> eines Faltungscodes kann mit der erweiterten Pfadgewichtsfunktion in geschlossener Form abgeschätzt werden: | |
| − | + | ::<math>{\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{ {\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1} } | |
| − | |||
| − | :<math>{\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1}} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Man spricht von der <b>Viterbi–Schranke</b>. Dabei leitet man die erweiterte Pfadgewichtsfunktion nach dem zweiten Parameter $U$ ab und setzt | + | Man spricht von der <b>Viterbi–Schranke</b>. Dabei leitet man die erweiterte Pfadgewichtsfunktion nach dem zweiten Parameter $U$ ab und setzt anschließend |
| + | *$X = \beta$, | ||
| + | *$U = 1$.}}<br> | ||
| − | [[ | + | ''Hinweis:'' In [[Aufgaben:Aufgabe_3.14:_Fehlerwahrscheinlichkeitsschranken|Aufgabe 3.14]] werden die ''Viterbi–Schranke'' und die ''Bhattacharyya–Schranke'' für den Rate–$1/2$–Standardcode und das [[Kanalcodierung/Klassifizierung_von_Signalen#Binary_Symmetric_Channel_.E2.80.93_BSC| BSC–Modell]] numerisch ausgewertet.<br> |
| − | + | [[Datei:P ID2716 KC T 3 5 S6b v2.png|right|frame|AWGN–Bitfehlerwahrscheinlichkeit von Faltungscodes]] | |
| − | *die | + | {{GraueBox|TEXT= |
| − | * | + | $\text{Beispiel 5:}$ Die Grafik verdeutlicht die gute Korrekturfähigkeit der Faltungscodes beim [[Kanalcodierung/Klassifizierung_von_Signalen#AWGN.E2.80.93Kanal_bei_bin.C3.A4rem_Eingang| AWGN–Kanal]]. |
| + | *Rote Kreise kennzeichnen die Bitfehlerrate für unseren Rate–$1/2$–Standardcode mit Memory $m = 2$.<br> | ||
| + | *Grüne Kreuze markieren einen Faltungscode mit $m = 6$, dem so genannten [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm#Definition_der_freien_Distanz| Industrie–Standardcode]].<br><br> | ||
| − | + | Insbesondere Codes mit großem Gedächtnis $m$ führen zu großen Gewinnen gegenüber uncodierter Übertragung (gestrichelte Kurve).}} | |
| − | |||
| − | |||
| − | + | == Aufgaben zum Kapitel == | |
| + | <br> | ||
| + | [[Aufgaben:Aufgabe_3.12:_Pfadgewichtsfunktion|Aufgabe 3.12: Pfadgewichtsfunktion]] | ||
| − | + | [[Aufgaben:Aufgabe_3.12Z:_Ring_und_Rückkopplung|Aufgabe 3.12Z: Ring und Rückkopplung]] | |
| − | |||
| − | [[Aufgaben: | ||
| − | [[ | + | [[Aufgaben:Aufgabe_3.13:_Nochmals_zu_den_Pfadgewichtsfunktionen|Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_3.14:_Fehlerwahrscheinlichkeitsschranken|Aufgabe 3.14: Fehlerwahrscheinlichkeitsschranken]] |
| − | + | ==Quellenverzeichnis== | |
| + | <references/> | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 1. Juli 2019, 14:25 Uhr
Inhaltsverzeichnis
- 1 Freie Distanz vs. Minimale Distanz
- 2 Pfadgewichtsfunktion
- 3 Erweiterte Pfadgewichtsfunktion
- 4 Pfadgewichtsfunktion aus Zustandsübergangsdiagramm
- 5 Regeln zur Manipulation des Zustandsübergangsdiagramms
- 6 Blockfehlerwahrscheinlichkeit vs. Burstfehlerwahrscheinlichkeit
- 7 Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke
- 8 Bitfehlerwahrscheinlichkeit und Viterbi–Schranke
- 9 Aufgaben zum Kapitel
- 10 Quellenverzeichnis
Freie Distanz vs. Minimale Distanz
Eine wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit linearer Blockcodes ist die minimale Distanz zwischen zwei Codeworten $\underline{x}$ und $\underline{x}\hspace{0.05cm}'$:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort $(\underline{0})$ beinhaltet. Zweckmäßigerweise setzt man deshalb $\underline{x}\hspace{0.05cm}' = \underline{0}$, so dass die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{0})$ das gleiche Ergebnis liefert wie das Hamming–Gewicht $w_{\rm H}(\underline{x})$.
$\text{Beispiel 1:}$ Die Tabelle zeigt die 16 Codeworte des $(7, 4, 3)$–Hamming–Codes
$($siehe $\text{Beispiel 7})$.
- Alle Codeworte außer dem Nullwort $(\underline{0})$ beinhalten mindestens drei Einsen ⇒ $d_{\rm min} = 3$.
- Es gibt sieben Codeworte mit drei Einsen (gelb hinterlegt), sieben mit vier Einsen (grün hinterlegt) und je eines ohne Einsen bzw. mit sieben Einsen.
Die freie Distanz $d_{\rm F}$ eines Faltungscodes (Convolution Code ⇒ $\mathcal{CC}$) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes:
- \[d_{\rm F}(\mathcal{CC}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]
In der Literatur wird anstelle von $d_{\rm F}$ teilweise auch $d_{∞}$ verwendet.
- Wesentlicher Unterschied zur minimalen Distanz ist, dass bei Faltungscodes nicht Informations– und Codeworte zu betrachten sind, sondern Sequenzen mit der Eigenschaft „semi–infinite”.
- Jede Codesequenz $\underline{x}$ beschreibt einen Pfad durch das Trellis.
- Die freie Distanz ist dabei das kleinstmögliche Hamming–Gewicht eines solchen Pfades (mit Ausnahme des Nullpfades).
Die Grafik zeigt drei der unendlich vielen Pfade mit dem minimalen Hamming–Gewicht $w_{\rm H, \ min}(\underline{x}) = d_{\rm F} = 5$.
Pfadgewichtsfunktion
Für jeden linearen Blockcode lässt sich wegen der endlichen Anzahl an Codeworten $\underline{x}$ in einfacher Weise eine Gewichtsfunktion angeben. Für das $\text{Beispiel 1}$ auf der letzten Seite lautet diese:
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]
Bei einem (nicht terminierten) Faltungscode kann keine solche Gewichtsfunktion angegegeben werden, da es unendlich viele, unendlich lange Codesequenzen $\underline{x}$ gibt, und damit auch unendlich viele Trellispfade. Um dieses Problem in den Griff zu bekommen, gehen wir nun von folgenden Voraussetzungen aus:
- Als Bezugsgröße für das Trellisdiagramm wählen wir stets den Pfad der Codesequenz $\underline{x} = \underline{0}$ und nennen diesen den Nullpfad $\varphi_0$.
- Wir betrachten nur noch solche Pfade $\varphi_j ∈ {\it \Phi}$, die alle zu einer vorgegebenen Zeit $t$ vom Nullpfad abweichen und irgendwann wieder zu diesem zurückkehren.
Obwohl nur ein Bruchteil aller Pfade zur Menge ${\it \Phi}$ gehören, beinhaltet ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} \}$ noch immer eine unbegrenzte Menge an Pfaden. $\varphi_0$ gehört nicht dazu.
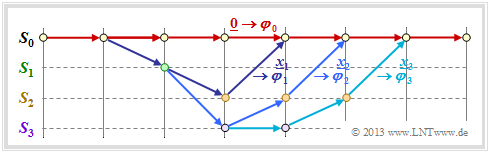
Im obigen Trellis sind einige Pfade $\varphi_j ∈ {\it \Phi}$ eingezeichnet:
- Der gelbe Pfad $\varphi_1$ gehört zur Sequenz $\underline{x}_1 = (11, 10, 11)$ mit dem Hamming–Gewicht $w_{\rm H}(\underline{x}_1) = 5$. Damit ist auch das Pfadgewicht $w(\varphi_1) = 5$. Aufgrund der Festlegung des Abzweigzeitpunktes $t$ hat nur noch dieser einzige Pfad $\varphi_1$ die freie Distanz $d_{\rm F} = 5$ zum Nullpfad ⇒ $A_5 = 1$.
- Für die beiden grünen Pfade mit den korrespondierenden Sequenzen $\underline{x}_2 = (11, 01, 01, 11)$ bzw. $\underline{x}_3 = (11, 10, 00, 10, 11)$ gilt $w(\varphi_2) = w(\varphi_3) = 6$. Kein anderer Pfad weist das Pfadgewicht $6$ auf. Wir berücksichtigen diese Tatsache durch den Koeffizienten $A_6 = 2$.
- Eingezeichnet ist auch der graue Pfad $\varphi_4$, assoziiert mit der Sequenz $\underline{x}_4 = (11, 01, 10, 01, 11)$ ⇒ $w(\varphi_4) = 7$. Auch die Sequenzen $\underline{x}_5 = (11, 01, 01, 00, 10, 11)$, $\underline{x}_6 = (11, 10, 00, 01, 01, 11)$ und $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$ haben das Pfadgewicht $7$ ⇒ $A_7 = 4$.
Damit lautet die Pfadgewichtsfunktion:
- \[T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} \hspace{0.05cm}.\]
Die Definition dieser Funktion $T(X)$ lautet:
$\text{Definition:}$ Für die Pfadgewichtsfunktion (englisch: Path Weight Enumerator Function, PWEF) eines Faltungscodes gilt:
- \[T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \hspace{0.05cm}.\]
- ${\it \Phi}$ bezeichnet die Menge aller Pfade, die den Nullpfad $\varphi_0$ genau zum festgelegten Zeitpunkt $t$ verlassen und (irgendwann) später zu diesem zurückkehren.
- Gemäß dem zweiten Gleichungsteil sind die Summanden nach ihren Pfadgewichten $w$ geordnet, wobei $A_w$ die Anzahl der Pfade mit Pfadgewicht $w$ bezeichnet.
- Die Summe beginnt mit $w = d_{\rm F}$.
- Das Pfadgewicht $w(\varphi_j)$ ist gleich dem Hamming–Gewicht (Anzahl der Einsen) der zum Pfad $\varphi_j$ assoziierten Codesequenz $\underline{x}_j$:
- \[w({\varphi_j) = w_{\rm H}(\underline {x} }_j) \hspace{0.05cm}.\]
Hinweis: Die für lineare Blockcodes definierte Gewichtsfunktion $W(X)$ und die Pfadgewichtsfunktion $T(X)$ der Faltungscodes weisen viele Gemeinsamkeiten auf; sie sind jedoch nicht identisch.
Wir betrachten nochmals die Gewichtsfunktion des $(7, 4, 3)$–Hamming–Codes,
- \[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},\]
und die Pfadgewichtsfunktion unseres Standard–Faltungscodierers,
- \[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} \]
Auffallend ist die „$1$” in der ersten Gleichung, die in der zweiten Gleichung fehlt. Das heißt: Bei den linearen Blockcodes wird das Bezugs–Codewort $\underline{x}_i = \underline{0}$ mitgezählt, wohingegen die Nullcodesequenz $\underline{x}_i = \underline{0}$ bzw. der Nullpfad $\varphi_0$ bei den Faltungscodes per Definition ausgeschlossen wird.
$\text{Persönliche Meinung des Autors:}$
Man hätte $W(X)$ ebenfalls ohne die „$1$” definieren können. Damit wäre unter anderem vermieden worden, dass sich die Bhattacharyya–Schranke für lineare Blockcodes und diejenge für Faltungscodes durch „$-1$” unterscheiden, wie aus den folgenden Gleichungen hervorgeht:
- Bhattacharyya–Schranke für lineare Blockcodes: ${\rm Pr(Blockfehler)} \le W(X = \beta) -1 \hspace{0.05cm},$
- Bhattacharyya–Schranke für Faltungscodes: ${\rm Pr(Burstfehler)} \le T(X = \beta) \hspace{0.05cm}.$
Erweiterte Pfadgewichtsfunktion
Die Pfadgewichtsfunktion $T(X)$ liefert nur Informationen hinsichtlich der Gewichte der Codesequenz $\underline{x}$.
- Mehr Informationen erhält man, wenn zusätzlich auch die Gewichte der Informationssequenz $\underline{u}$ erfasst werden.
- Man benötigt dann zwei Formalparameter $X$ und $U$, wie aus der folgenden Definition hervorgeht.
$\text{Definition:}$ Die erweiterte Pfadgewichtsfunktion (englisch: Enhanced Path Weight Enumerator Function, EPWEF) lautet:
- \[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
Es gelten alle Angaben zur $T(X)$–Definition auf der letzten Seite. Zusätzlich ist zu beachten:
- Das Pfadeingangsgewicht $u(\varphi_j)$ ist gleich dem Hamming–Gewicht der zum Pfad $\varphi_j$ assoziierten Informationssequenz $\underline{u}_j$. Es wird als Potenz des Formalparameters $U$ ausgedrückt.
- Der Koeffizient $A_{w, \ u}$ bezeichnet die Anzahl der Pfade $\varphi_j$ mit dem Pfadausgangsgewicht $w(\varphi_j)$ und dem Pfadeingangsgewicht $u(\varphi_j)$. Als Laufvariable für den zweiten Anteil wird $u$ verwendet.
- Setzt man in der erweiterten Pfadgewichtsfunktion den Formalparameter $U = 1$, so ergibt sich die ursprüngliche Gewichtsfunktion $T(X)$ gemäß der Definition auf der letzten Seite.
Bei vielen (und allen relevanten) Faltungscodes lässt sich obere Gleichung noch vereinfachen:
- \[T_{\rm enh}(X, U) =\hspace{0.1cm} \sum_{w \ = \ d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]
$\text{Beispiel 2:}$ Die erweiterte Pfadgewichtsfunktion unseres Standardcodieres lautet somit:
- \[T_{\rm enh}(X, U) = U \cdot X^5 + 2 \cdot U^2 \cdot X^6 + 4 \cdot U^3 \cdot X^7+ \text{ ...} \hspace{0.1cm} \hspace{0.05cm}.\]
Vergleicht man dieses Ergebnis mit dem unten dargestellten Trellis, so erkennt man:
- Der gelb hinterlegte Pfad – gekennzeichnet durch $X^5$ – setzt sich aus einem blauen Pfeil $(u_i = 1)$ und zwei roten Pfeilen $(u_i = 0)$ zusammen. Somit wird aus $X^5$ der erweiterte Term $UX^5$.
- Die Sequenzen der beiden grünen Pfade sind $\underline{u}_2 = (1, 1, 0, 0)$ ⇒ $\underline{x}_2 = (11, 01, 01, 11)$ sowie $\underline{u}_3 = (1, 0, 1, 0, 0)$ ⇒ $\underline{x}_3 = (11, 10, 00, 10, 11)$. Daraus ergibt sich der zweite Term $2 \cdot U^2X^6$.
- Der graue Pfad (und die drei nicht gezeichneten Pfade) ergeben zusammen den Beitrag $4 \cdot U^3X^7$. Jeder dieser Pfade beinhaltet drei blaue Pfeile ⇒ drei Einsen in der zugehörigen Informationssequenz.
Pfadgewichtsfunktion aus Zustandsübergangsdiagramm
Es gibt eine elegante Methode, um die Pfadgewichtsfunktion $T(X)$ und deren Erweiterung direkt aus dem Zustandsübergangsdiagramm zu bestimmen. Dies soll hier und auf den folgenden Seiten am Beispiel unseres Standardcodierers demonstriert werden.
Zunächst muss dazu das Zustandsübergangsdiagramm umgezeichnet werden. Die Grafik zeigt dieses links in der bisherigen Form als Diagramm $\rm (A)$, während rechts das neue Diagramm $\rm (B)$ angegeben ist.
Man erkennt:
- Der Zustand $S_0$ wird aufgespalten in den Startzustand $S_0$ und den Endzustand $S_0\hspace{0.01cm}'$. Damit lassen sich alle Pfade des Trellisdiagramms, die im Zustand $S_0$ beginnen und irgendwann zu diesem zurückkehren, auch im rechten Graphen $\rm (B)$ nachvollziehen. Ausgeschlossen sind dagegen direkte Übergänge von $S_0$ nach $S_0\hspace{0.01cm}'$ und damit auch der Nullpfad $($Dauer–$S_0)$.
- Im Diagramm $\rm (A)$ sind die Übergänge anhand der Farben Rot $($für $u_i = 0)$ und Blau $($für $u_i = 1)$ unterscheidbar, und die Codeworte $\underline{x}_i ∈ \{00, 01, 10, 11\}$ sind an den Übergängen vermerkt. Im neuen Diagramm $\rm (B)$ werden $(00)$ durch $X^0 = 1$ und $(11)$ durch $X^2$ ausgedrückt. Die Codeworte $(01)$ und $(10)$ sind nun nicht mehr unterscheidbar, sondern werden einheitlich mit $X$ bezeichnet.
- Anders formuliert: Das Codewort $\underline{x}_i$ wird nun als $X^w$ dargestellt, wobei $X$ eine dem Ausgang (der Codesequenz) zugeordnete Dummy–Variable ist und $w = w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht des Codewortes $\underline{x}_i$ angibt. Bei einem Rate–$1/2$–Code ist der Exponent $w$ entweder $0, \ 1$ oder $2$.
- Ebenfalls verzichtet wird im Diagramm $\rm (B)$ auf die Farbcodierung. Das Informationsbit $u_i = 1$ wird nun durch $U^1 = U$ und das Informationsbit $u_i = 0$ durch $U^0 = 1$ gekennzeichnet. Die Dummy–Variable $U$ ist also der Eingangssequenz $\underline{u}$ zugeordnet.
Regeln zur Manipulation des Zustandsübergangsdiagramms
Ziel unserer Berechnungen wird es sein, den (beliebig komplizierten) Weg von $S_0$ nach $S_0\hspace{0.01cm}'$ durch die erweiterte Pfadgewichtsfunktion $T_{\rm enh}(X, \ U)$ zu charakterisieren. Dazu benötigen wir Regeln, um den Graphen schrittweise vereinfachen zu können.
Serielle Übergänge
Zwei serielle Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – können durch eine einzige Verbindung mit dem Produkt dieser Bewertungen ersetzt werden.
Parallele Übergänge
Zwei parallele Verbindungen – gekennzeichnet durch $A(X, \ U)$ und $B(X, \ U)$ – werden durch die Summe ihrer Bewertungsfunktionen zusammengefasst.
Ring
Die nebenstehende Konstellation kann durch eine einzige Verbindung ersetzt werden, wobei für die Ersetzung gilt:
- \[E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.\]
Rückkopplung
Durch die Rückkopplung können sich hier zwei Zustände beliebig oft abwechseln. Für diese Konstellation gilt:
- \[F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} \hspace{0.05cm}.\]
Die hier angegebenen Gleichungen für Ring und Rückkopplung sind in der Aufgabe 3.12Z zu beweisen.
$\text{Beispiel 3:}$ Die oben genannten Regeln sollen nun auf unser Standardbeispiel angewendet werden. In der Grafik sehen Sie links das modifizierte Diagramm $\rm (B)$.
- Zunächst ersetzen wir den rot hinterlegten Umweg von $S_1$ nach $S_2$ über $S_3$ im Diagramm $\rm (B)$ durch die im Diagramm $\rm (C)$ eingezeichnete rote Verbindung $T_1(X, \hspace{0.05cm} U)$. Es handelt sich nach der oberen Klassifizierung um einen „Ring” mit den Beschriftungen $A = C = U \cdot X$ und $B = X$, und wir erhalten für die erste Reduktionsfunktion:
- \[T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} \hspace{0.05cm}.\]
- Nun fassen wir die parallelen Verbindungen entsprechend der blauen Hinterlegung im Diagramm $\rm (C)$ zusammen und ersetzen diese durch die blaue Verbindung im Diagramm $\rm (D)$. Die zweite Reduktionsfunktion lautet somit:
- \[T_2(X, \hspace{0.05cm}U) = T_1(X, \hspace{0.05cm}U) + X = \frac{U X^2 + X \cdot (1-UX)}{1- U X} = \frac{X}{1- U X} \hspace{0.05cm}.\]
- Der gesamte Graph $\rm (D)$ kann dann durch eine einzige Verbindung von $S_0$ nach $S_0\hspace{0.01cm}'$ ersetzt werden. Nach der Rückkopplungsregel erhält man für die erweiterte Pfadgewichtsfunktion:
- \[T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} \hspace{0.05cm}.\]
- Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $ lässt sich hierfür auch schreiben:
- \[T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \big [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.\]
- Setzt man die formale Input–Variable $U = 1$, so erhält man die „einfache” Pfadgewichtsfunktion, die allein Aussagen über die Gewichtsverteilung der Ausgangssequenz $\underline{x}$ erlaubt:
- \[T(X) = X^5 \cdot \big [ 1 + 2 X + 4 X^2 + 8 X^3 +\text{...}\hspace{0.05cm} \big ] \hspace{0.05cm}.\]
- Das gleiche Ergebnis haben wir bereits aus dem Trellisdiagramm auf der Seite Pfadgewichtsfunktion abgelesen. Dort gab es einen grauen Pfad mit Gewicht $5$, zwei gelbe Pfade mit Gewicht $6$ und vier grüne Pfade mit Gewicht $7$.
Blockfehlerwahrscheinlichkeit vs. Burstfehlerwahrscheinlichkeit
Das einfache Modell gemäß der Skizze gilt sowohl für lineare Blockcodes als auch für Faltungscodes.
Blockcodes
Bei den Blockcodes bezeichnen $\underline{u} = (u_1, \ \text{...} \hspace{0.05cm}, \ u_i, \ \text{...} \hspace{0.05cm}, \ u_k)$ und $\underline{v} = (v_1, \ \text{...} \hspace{0.05cm}, v_i, \ \text{...} \hspace{0.05cm} \ , \ v_k)$ die Informationsblöcke am Eingang und Ausgang des Systems.
Damit sind folgende Beschreibungsgrößen angebbar:
- die Blockfehlerwahrscheinlichkeit ${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} ≠ \underline{u}),$
- die Bitfehlerwahrscheinlichkeit ${\rm Pr(Bitfehler)} = {\rm Pr}(v_i ≠ u_i).$
$\text{Bitte beachten Sie:}$ Bei realen Übertragungssystemen gilt aufgrund des thermischen Rauschens stets:
- $${\rm Pr(Bitfehler)} > 0\hspace{0.05cm},\hspace{1.0cm}{\rm Pr(Blockfehler)} > {\rm Pr(Bitfehler)} \hspace{0.05cm}.$$
Hierfür ein einfacher Erklärungsversuch: Entscheidet der Decoder in jedem Block der Länge $k$ genau ein Bit falsch,
- so beträgt auch die mittlere Bitfehlerwahrscheinlichkeit ${\rm Pr(Bitfehler)}= 1/k$,
- während für die Blockfehlerwahrscheinlichkeit ${\rm Pr(Blockfehler)}\equiv 1$ gilt.
Faltungscodes
Bei Faltungscodes ist die Blockfehlerwahrscheinlichkeit nicht angebbar, da hier $\underline{u} = (u_1, \ u_2, \ \text{...} \hspace{0.05cm})$ und $\underline{\upsilon} = (v_1, \ v_2, \ \text{...} \hspace{0.05cm})$ Sequenzen darstellen.
Selbst der kleinstmögliche Codeparameter $k = 1$ führt hier zur Sequenzlänge $k \hspace{0.05cm}' → ∞$, und die Blockfehlerwahrscheinlichkeit ergäbe sich stets zu ${\rm Pr(Blockfehler)}\equiv 1$, selbst wenn die Bitfehlerwahrscheinlichkeit extrem klein (aber ungleich Null) ist.
$\text{Definition:}$ Für die Burstfehlerwahrscheinlichkeit eines Faltungscodes gilt:
- \[{\rm Pr(Burstfehler)} = {\rm Pr}\big \{ {\rm Decoder\hspace{0.15cm} verl\ddot{a}sst\hspace{0.15cm} zur\hspace{0.15cm} Zeit}\hspace{0.15cm}t \hspace{0.15cm}{\rm den \hspace{0.15cm}korrekten \hspace{0.15cm}Pfad}\big \} \hspace{0.05cm}.\]
- Um für die folgende Herleitung die Schreibweise zu vereinfachen, gehen wir stets von der Nullsequenz $(\underline{0})$ aus, die im gezeichneten Trellis als Nullpfad $\varphi_0$ rot dargestellt ist.
- Alle anderen Pfade $\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} $ (und noch viele mehr) verlassen $\varphi_0$ zur Zeit $t$. Sie alle gehören zur Pfadmenge ${\it \Phi}$ ⇒ „Viterbi–Decoder verlässt den korrekten Pfad zur Zeit $t$”. Diese Wahrscheinlichkeit wird auf der nächsten Seite berechnet.
Burstfehlerwahrscheinlichkeit und Bhattacharyya–Schranke
Wir gehen wie im früheren Kapitel Schranken für die Blockfehlerwahrscheinlichkeit von der paarweisen Fehlerwahrscheinlichkeit ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ aus, dass der Decoder anstelle des Pfades $\varphi_0$ den Pfad $\varphi_i$ auswählen könnte. Alle betrachteten Pfade $\varphi_i$ verlassen den Nullpfad $\varphi_0$ zum Zeitpunkt $t$; sie gehören somit alle zur Pfadmenge ${\it \Phi}$.
Die gesuchte Burstfehlerwahrscheinlichkeit ist gleich der folgenden Vereinigungsmenge:
- \[{\rm Pr(Burstfehler)}= {\rm Pr}\left (\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}\big] \hspace{0.05cm}\cup\hspace{0.05cm}\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}\big]\hspace{0.05cm}\cup\hspace{0.05cm} \text{... }\hspace{0.05cm} \right )= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} \big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big] \right )\hspace{0.05cm}.\]
Eine obere Schranke hierfür bietet die so genannte Union–Bound:
- \[{\rm Pr(Burstfehler)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} {\rm Pr}\big [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big ] = {\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{0.05cm}.\]
Die paarweise Fehlerwahrscheinlichkeit kann mit der Bhattacharyya–Schranke abgeschätzt werden:
- \[{\rm Pr}\big [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\big ] \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] \le \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.\]
Hierbei bezeichnet
- $w_{\rm H}(\underline{x}_i)$ das Hamming–Gewicht der möglichen Codesequenz $\underline{x}_i,$
- $\ w(\varphi_i)$ das Pfadgewicht des entsprechenden Pfades $\varphi_i ∈ {\it \Phi}$, und
- $\beta$ den so genannten Bhattacharyya–Kanalparameter.
Durch Summation über alle Pfade und einen Vergleich mit der (einfachen) Pfadgewichtsfunktion $T(X)$ erhalten wir das Ergebnis:
- \[{\rm Pr(Burstfehler)} \le T(X = \beta),\hspace{0.5cm}{\rm mit}\hspace{0.5cm} T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.\]
$\text{Beispiel 4:}$ Für unseren Standardcodierer ⇒ $R = 1/2, \ \ m = 2, \ \ \mathbf{G}(D) = (1 + D + D^2, \ 1 + D)$ haben wir folgende Pfadgewichtsfunktion erhalten:
- \[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + \ \text{...} \hspace{0.1cm} = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ \ \text{...} \hspace{0.1cm}) \hspace{0.05cm}.\]
Mit der Reihenentwicklung $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \hspace{0.15cm} $ kann hierfür auch geschrieben werden:
- \[T(X) = \frac{X^5}{1-2 \cdot X} \hspace{0.05cm}.\]
Das BSC–Modell liefert mit der Verfälschungswahrscheinlichkeit $\varepsilon$ folgende Bhattacharyya–Schranke:
- \[{\rm Pr(Burstfehler)} \le T(X = \beta) = T\big ( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)} \big ) = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.\]
In der Aufgabe 3.14 soll diese Gleichung numerisch ausgewertet werden.
Bitfehlerwahrscheinlichkeit und Viterbi–Schranke
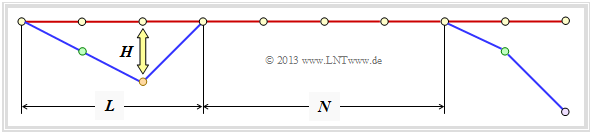
Abschließend wird eine obere Schranke für die Bitfehlerwahrscheinlichkeit angegeben. Gemäß der Grafik gehen wir wie in [Liv10][1] von folgenden Gegebenheiten aus:
- Gesendet wurde die Nullsequenz $\underline{x} = \underline{0}$ ⇒ Pfad $\varphi_0$.
- Die Dauer einer Pfadabweichung (englisch: Error Burst Duration ) wird mit $L$ bezeichnet.
- Den Abstand zweier Bursts (englisch: Inter–Burst Time ) nennen wir $N$.
- Das Hamming–Gewicht des Fehlerbündels sei $H$.
Für einen Rate–$1/n$–Faltungscode ⇒ $k = 1$, also einem Informationsbit pro Takt, lässt sich aus den Erwartungswerten ${\rm E}\big[L \big]$, ${\rm E}\big[N \big]$ und ${\rm E}\big[H\big]$ der oben definierten Zufallsgrößen eine obere Schranke für die Bitfehlerwahrscheinlichkeit angeben:
- \[{\rm Pr(Bitfehler)} = \frac{{\rm E}\big[H\big]}{{\rm E}[L] + {\rm E}\big[N\big]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}\big[H\big]}{{\rm E}\big[N\big]} \hspace{0.05cm}.\]
Hierbei ist vorausgesetzt, dass
- die (mittlere) Dauer eines Fehlerbündels in der Praxis sehr viel kleiner ist als der zu erwartende Abstand zweier Bündel,
- die (mittlere) Inter–Burst Time $E\big[N\big]$ gleich dem Kehrwert der Burstfehlerwahrscheinlichkeit ist,
- der Erwartungswert im Zähler wie folgt abgeschätzt wird:
- \[{\rm E}\big[H \big] \le \frac{1}{\rm Pr(Burstfehler)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
Bei der Herleitung dieser Schranke werden die paarweise Fehlerwahrscheinlichkeit ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$ sowie die Bhattacharyya–Abschätzung verwendet. Damit erhält man mit
- dem Pfadeingangsgewicht $u(\varphi_i),$
- dem Pfadausgangsgewicht $w(\varphi_i),$ und
- dem Bhattacharyya–Parameter $\beta$
die folgende Abschätzung für die Bitfehlerwahrscheinlichkeit und bezeichnet diese als die Viterbi–Schranke:
- \[{\rm Pr(Bitfehler)}\le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]
Dieses Zwischenergebnis lässt sich auch in anderer Form darstellen. Wir erinnern uns an die erweiterte Pfadgewichtsfunktion
- \[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.05cm}.\]
Leitet man diese Funktion nach der Dummy–Eingangsvariablen $U$ ab, so erhält man
- \[\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} \hspace{0.05cm}.\]
Setzen wir schließlich noch für die Dummy–Eingangsvariable $U = 1$, so erkennen wir den Zusammenhang zum obigen Ergebnis:
- \[\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.\]
$\text{Fazit:}$ Die Bitfehlerwahrscheinlichkeit eines Faltungscodes kann mit der erweiterten Pfadgewichtsfunktion in geschlossener Form abgeschätzt werden:
- \[{\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{ {\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1} } \hspace{0.05cm}.\]
Man spricht von der Viterbi–Schranke. Dabei leitet man die erweiterte Pfadgewichtsfunktion nach dem zweiten Parameter $U$ ab und setzt anschließend
- $X = \beta$,
- $U = 1$.
Hinweis: In Aufgabe 3.14 werden die Viterbi–Schranke und die Bhattacharyya–Schranke für den Rate–$1/2$–Standardcode und das BSC–Modell numerisch ausgewertet.
$\text{Beispiel 5:}$ Die Grafik verdeutlicht die gute Korrekturfähigkeit der Faltungscodes beim AWGN–Kanal.
- Rote Kreise kennzeichnen die Bitfehlerrate für unseren Rate–$1/2$–Standardcode mit Memory $m = 2$.
- Grüne Kreuze markieren einen Faltungscode mit $m = 6$, dem so genannten Industrie–Standardcode.
Insbesondere Codes mit großem Gedächtnis $m$ führen zu großen Gewinnen gegenüber uncodierter Übertragung (gestrichelte Kurve).
Aufgaben zum Kapitel
Aufgabe 3.12: Pfadgewichtsfunktion
Aufgabe 3.12Z: Ring und Rückkopplung
Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen
Aufgabe 3.14: Fehlerwahrscheinlichkeitsschranken
Quellenverzeichnis
- ↑ Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.